мат. модел в почв

Часть II. Применение математических моделей в почвоведении

5.4.2. Модель КДП с двумя центрами сорбции

Идея подхода заключается в том, что вместо того, чтобы раз бивать поровое пространство на проводящую и застойную зону, можно поступить проще. Вводят два механизма сорбции – мгно венную и кинетическую. Физическим оправданием является на личие в почве разных минералов, органического вещества, окси дов алюминия и железа и пр., которые избирательно и с разной интенсивностью взаимодействуют с переносимыми химическими веществами. Для упрощения модели предлагается разделить все типы взаимодействия на два:

1.Мгновенное, описываемое уравнением линейной равно весной сорбции;

2.Кинетическое, с линейной изотермой сорбции 1 го поряд

ка.

Подход для описания сложного процесса сорбции во многом формальный, никто не знает методов определения числа (кон центрации) центров мгновенного (равновесного) и кинетического (динамического) равновесия, однако, этот подход применяется повсеместно в разных моделях.

Мгновенный обмен приписывается центрам сорбции 1 го ти па и выражается уравнением:

где F – доля центров 1 го типа в общей сорбционной площади. Для описания кинетического взаимодействия центров 2 го

типа используется уравнение неравновесного обмена вещества, которые находятся в растворенном и сорбированном виде:

где CS1 и CS2 – сорбированное количество химиката центрами 1

го и 2 го типа.

331

Математическое моделирование в почвоведении

Для описания динамической сорбции используют уравнение кинетики 1 го порядка (функция экспоненциально убывающая). Также считается, что сорбция на сорбционных центрах 1 го типа происходит мгновенно (в уравнении нет параметра времени), это сорбция всегда равновесный процесс. На центрах 2 го типа, кото рые сорбируют по кинетике 1 го порядка, происходит неравно весная динамическая сорбция.

Приведенные уравнения и способы их решения представляют далеко неполный арсенал современных аналитических методов расчета параметров моделей КДП химических веществ в почве. Следует заметить, что стандартные процедуры для решения этих уравнений существуют и периодически дополняются на протяже нии последних 25 лет. Многие исследователи активно используют программы CFITIM ван Генухтена. Однако даже относительно простые уравнения могут поставить в тупик неподготовленного пользователя.

Кинетические уравнения принято также использовать для описания обмена веществом между проточными и застойными зонами порового пространства почвы:

5.4.3.Отрицательная адсорбция

Вразличных лабораторных экспериментах и при модельных расчетах было замечено, что анионы (как впрочем, любые веще ства, несущие отрицательный заряд, например, агрохимикаты или пестициды) имеют некоторые особенности миграции. Эти веще ства появляются на выходе из колонки раньше, чем не несущие заряда вещества. Образно говоря, для анионов поровое про странство, сквозь которое они мигрируют, несколько «сужается». Физики почв, давно указывали, что в почве имеется так называе мый «нерастворяющий» объем, или «объем выталкивания» анионов, поскольку твердофазная стенка в почве, как правило,

332

Часть II. Применение математических моделей в почвоведении

несет отрицательный заряд, такой же как и анион. Происходит явление «отрицательной адсорбции» анионов. Как ввести это яв ление в модель? Как мы уже знаем, надо представить физический механизм явления, а затем ввести его в качестве эксперимен тального физического параметра в математическую модель и ее уравнения.

Действительно, раз это явление связано с некоторым объе мом воды около твердой фазы почвы (объем выталкивания анио нов), то, видимо, удобнее всего и выразить его в виде некоторой влажности. Влага, составляющая часть заполняющей пору, не со держит анионы и не является для них проводящим пространст вом. Ее нужно исключить из проводящего ионы порового про странства. Эта влажность была названа влажностью нераство ряющего объема – θ [безразмерная величина или см3/см3].

Физики почв давно используют методы определения нерас творяющего объема влаги (Шеин, 2005). В одном из методов сравнивают вводимую концентрацию иона Cl– и получающуюся после взаимодействия с почвой. Образовавшаяся после взаимо действия с почвой равновесная концентрация иона Cl–несколько выше вводимой, и вот по разнице концентраций можно рассчи тать влажность почвы, которая не содержит ион Cl– или объем вы талкивания. Теперь все системно уложилось сообразно физике явления. Согласно физическому параметру, характеризующему это явление, можно ввести этот параметр в уравнение КДУ. Урав нение в этом случае выглядит:

где (θ−θ* ) – представляет собой объем влаги, проводящий анионы в поровом пространстве почв.

Отметим, что в большинстве программных продуктов эта ве личина называется «диффузивность». Она близка к величине МГ для исследуемых почв или к величине θr – остаточной влажности, представленной в уравнении ван Генухтена.

333

Математическое моделирование в почвоведении

Итак, в случае необходимости расчета передвижения солей (ионов или незаряженных частиц) в профиле почвы, необходимо заполнить таблицу, касающуюся физического экспериментально го обеспечения солепереноса. В простейшем случае, эта табличка будет иметь вид:

Таблица II.5.1

Пример гидрохимических параметров почвы при моделировании со лепереноса в слоистой почве

Примечания. D* – гидродинамическая диффузия, λ – шаг смешения, θ* – нерас творяющий объем, F – доля центров сорбции 1 го типа, KF – константа равнове сия между веществом в жидкой и твердой фазах (константа Фрейндлиха).

*Приведены примеры экспериментального обеспечения для почвенных слоев минеральных почв, слой 2 облегчен по гранулометрическому составу

5.4.4. Граничные условия в моделях солепереноса

Итак, мы рассмотрели все важнейшие явления, входящие в составляющую «источник/сток» конвективно диффузионного уравнения: это сорбция (равновесная и динамическая), распад или разложение вещества по динамическим кривым распада (разного порядка, от нулевого до n ого), потери вещества за счет его испарения. Однако, как и в случае движения воды, расчетная схема требует задания граничных условий (условия на границах почвенной толщи). Хотя теоретически они задаются аналогично описанным выше граничным условиям для расчетов водных про цессов.

334

Часть II. Применение математических моделей в почвоведении

Понятно, что для описания солепереноса (переноса веществ), начальными условиями будут распределение концентрации ве щества по рассматриваемому профилю почвы.

Для солепереноса применяются два типа граничных условий

– это условия Дирихле и Коши Условие 1 го типа (условие Дирихле) задает концентрацию:

c(x,t) =c0 (x,t) при x =0 (на поверхности) или x =L (на ниж ней границе профиля).

Условие 3 го рода (условие Коши) задает поток солей на верхней или нижней границах:

−θ D ∂c +qc =q0c0 при x =0 или x =L .

∂x

При этом q0 – представляет восходящий поток, имеющий концентрацию исследуемого вещества с0 [моль/л]. В некоторых случаях, когда мы имеем непроницаемый нижний слой (q0=0) или когда поток выводится прямо из рассматриваемого профиля, то это условие (условие 3 го рода или Коши) превращается в условие 2 го рода (условие Неймана) и граничные условия описываются следующим образом:

335

Математическое моделирование в почвоведении

5.5. Диффузия веществ в газовой форме. Потери за счет испарения

Следует отметить еще одни процесс, входящий в КДУ в виде составляющей «источник/сток» или просто «сток». Это потеря ве щества в газовой форме, его испарение. Процесс весьма заметен при описании переноса пестицидов, так как эти сложные вещест ва способны выделяться в газовую фазу из раствора и далее диф фундировать до верхних почвенных слоев. Это физическое описа ние испарение вещества. Рассмотрим описание этого процесса в математическом виде.

Диффузия вещества в газовой форме описывается в виде уравнения Фика:

где Jp – массовый поток за счет испарения вещества [кг/(м2сут)],

Сg – концентрация вещества в газовой фазе в верхнем слое почвы [кг/м3], rs,v – сопротивление почвы в поверхностном слое [сут/м], ra,v – сопротивление воздуха в верхнем граничном условии.

Сопротивление rs,v в газовой среде почвы рассматривают по

где ds и da – толщина ламинарного слоя в верхнем граничном ус ловии, Da,s , Da – коэффициенты диффузии вещества в почвенном воздухе и воздухе, соответственно [м2/сут].

336

Часть II. Применение математических моделей в почвоведении

5.6. Другие блоки (модули) почвенных гидротермических моделей переноса веществ в почве

В главе, посвященной движению влаги в почве, мы познако мились с уравнением Ричардса. Вспомним, что в уравнении вла гопереноса Ричардса

C(θ,Pк с) ∂∂Pкtс = ∂∂z Квл(Pк с) ∂∂Pкzс −1 ±I

имеется составляющая I – «источник/сток», которая также имеет размерность потока и отражает поглощение влаги из указанного слоя почвы корнями растений (тогда он отрицательный), или же, например, боковой внутрипочвенный приток (положительный). В большинстве моделей влагопереноса требуется описать влаго потребление корнями растений, как одну из самых заметных ба лансовых составляющих.

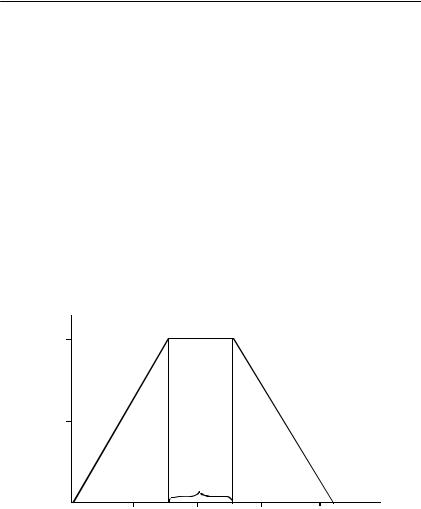
Обычно транспирацию растительного сообщества (Tr, см/сут) рассматривают как функцию давления почвенной влаги в виде так называемой «транспирационной трапеции». Такое описание бы ло предложено голландским ученым Р.А. Феддесом с коллегами (Feddes et al., 1978). Водопотребление полагают равным нулю при значениях давления влаги близких к 0, а также при значениях давления близких к точке завядания ( 15000 см водн. ст). Опти мальное, близкое к потенциальной испаряемости, водопотребле ние находится в диапазоне давлений влаги от давления барботи рования (Рб) до критического (Ркр). При давлениях влаги от 0 до Рб и от Ркр до точки завядания водопотребление изменяется линейно с давлением влаги.

Это характерная зависимость обусловлена физическими за кономерностями работы устьичного аппарата растений. Устьица растений ограничивают выделение влаги в случае, если растение страдает от избытка влаги или при ее недостатке. Если же давле ние влаги в почве находится в оптимальном диапазоне (обычно в диапазоне от –300 до –600 – 800 см водного столба), то транспи

337

Математическое моделирование в почвоведении

рация находится на уровне Tr0 и равна испаряемости с открытой водной поверхности. Эти закономерности влагопотребления рас тений приведены на рис. II.5.6.

На «транспирационной трапеции» имеются две важные точки

– давление входа воздуха или «давление барботирования» (Pб) и так называемое «критическое давление влаги» (Ркр), при котором устьица растений закрываются за счет наступающей почвенной засухи. Эти две величины служат экспериментальным обеспече нием моделей для описания транспирации растений. Нередко эти величины, подчеркивая их физический смысл, называют: точка уменьшения транспирации в условиях около насыщения (Рб) и точка уменьшения транспирации в засушливой области (Ркр – дав ление «влаги завядания»).

Tr/Tr0

1.0

0.5

Капиллярно-сорбционное давление влаги

Рис. II.5.6. «Транспирационная трапеция»

Суммарную транспирацию растений необходимо еще рас пределить по почвенным слоям. Это распределение осуществля ют в соответствие с транспирационной трапецией и концентраци ей корней в каждом из рассматриваемых почвенных слоев. Таким образом рассчитывают величину корневого потребления или ве личину «стока» I в уравнении влагопереноса:

338

Часть II. Применение математических моделей в почвоведении

где ω – функция влагопотребления корней в рассматриваемой почвенной толще, R – функция «транспирационной трапеции», включающая две основные точки перегиба Рб и Ркр, которые ис следователь должен включать в модель в качестве эксперимен тального обеспечения, zr – глубина корнеобитаемой зоны.

Функцию влагопотребления ω, как правило, берут как распре деление массы (длины) корней в единице объема почвы по глуби не z и во времени t (с учетом роста корней в течение вегетационно го сезона). Для этого, конечно, необходимы экспериментальные данные для конкретной культуры, для конкретного растения или ценоза в целом. Такое распределение корневой массы тоже, как правило, входятвэкспериментальноеобеспечениемоделей.

Максимально возможная величина водопотребления корней, которая складывается из потребления влаги по всем почвенным слоям, равна потенциальной транспирации на рис. II.5.6. Это ве личина – Т0. Потенциальное водопотребление корней из конкрет ного слоя почвы рассчитывается по относительной объемной длине корней [м/м3], которая представляет часть от их общей объемной длины в рассматриваемом профиле. Следовательно, для моделей необходим еще один экспериментально опреде ляемый параметр – относительное распределение корней в рас сматриваемом профиле почвы (от верхней до нижней границы расчета). Экспериментальное определение этой величины – труд ная задача, а при динамическом моделировании необходимо учитывать еще и рост корней, т.е. учитывать изменение во време ни распределения корней по профилю. В большинстве моделей имеют подсказки для разного типа растений и примерных усло вий их роста, но это может снизить точность моделирования.

Итак, для расчета потребления влаги корнями необходимо знать еще одну величину – потенциальную транспирацию расте

339

Математическое моделирование в почвоведении

ний Т0. В зависимости от почвенных условий (засуха, или напротив избыток воды уменьшают потенциальную транспирацию) в соот ветствии с законом «трапеции» (законом Феддеса). Эту величину можно корректировать, но величину Т0 нужно использовать как основную.

Далее будем говорить о величине ЕТ0 – потенциальной эва потранспирации, т.е. не только о транспирации растений, но и об испарении из почвы. Проблема заключается в том, как рассчитать эту величину по метеопараметрам (данные метеослужбы за тот иной период времени). Важно понимать, какие основные пара метры нужно использовать для расчета, чтобы избежать возмож ных ошибок при расчете или несогласованности в методиках.

Как правило, для расчетов ЕТ0 используют уравнения Пенма на Монтейта. Это уравнение, рекомендованное FAO в 1990 году для расчетов эвапотранспирации, выглядит следующим образом:

где ET0 – эвапотранспирация [мм/cут], ETrad – радиационная со ставляющая эвапотранспирации [мм/cут], ETaero – аэродинамиче ская составляющая [мм/cут], λ – скрытое тепло парообразования [МДж/кг], R – чистая радиация на поверхности почвы [МДж/(м2сут)], G – поток тепла в почву [МДж/(м2сут)], ρ – плот ность воздуха, сv – удельная теплота влажного воздуха (принима ется равной 1.013 [кДж/(кг Со)]), (e0 −et ) – дефицит относительно го давления воздуха [кПа], ео – давление паров воды при темпе ратуре Т [кПа], еd – реальное давление паров воды, r – сопротив ление травяного покрова [с/м], ra – аэродинамическое сопротив ление [c/м]. Угол наклона кривой давления паров воды и пси хрометрическая константа γ также рассчитываются по определен ным формулам, в которых используются традиционные метеопа раметры. При современных средствах расчета и информационных ресурсах современных метеопостов соответствующая информа

340