мат. модел в почв

Часть II. Применение математических моделей в почвоведении

Казалось бы, что на всем поле значений b1 и b2 значение 0.28 и является минимальным, так как в других узлах значения выше, а нам ведь надо найти минимум среднеквадратичной ошибки. Од нако, если «измельчить» сетку, рассчитать значения параметров в ближайших точках, то можно найти такую точку, вокруг которой все значения на рассматриваемом поле параметров будут увели чиваться. Достигнут минимум Sr в рассматриваемом поле пара метров. Для точки достигнутого минимума мы и определяем b1 и b2. В данном случае они равны b1= 0.628 и b2 =0.401. Таким обра зом, искомое уравнение после операции сканирования приобре

Заметим, что во время операции сканирования мы сделали очень важный шаг: мы начали наши расчеты с конкретных значе ний b1 и b2. Мы их задали равными 0.3. Эти значения называют «начальные приближения». Задавать их – большое искусство. Ес ли их задать совсем другими, мы окажемся совсем в другом мес те рассматриваемого поля и по мере движения («дробления сет ки») можем оказаться не в генеральном минимуме, а в так назы ваемом «локальном минимуме», что будет серьезной ошибкой. Даже современные расчетные программы в этом случае «зависа ют» и не находят нужного решения. Значит нужно научиться под бирать правильные (близкие к реальным) начальные приближе ния. В расчетных программах обычно «зашиты» некие начальные приближения. Но они могут привести к «локальному минимуму» и сбою в решении. Как же достичь решения в этом случае? Лучше всего самому задать предполагаемые начальные приближения на основе анализа графика. В степенном уравнении параметр b2 от вечает за угол наклона, а b1 – за положение кривой («выше ниже»). Из графика видно, что по оси ординат он пересекает об ласть значений 0.5–1.0. Соответственно начальное значение b1 нужно взять из этой области, и также из графика определить при мерный угол наклона. Если взять эти значения как начальное приближение, аппроксимация пройдет более успешно, и мы по

291

Математическое моделирование в почвоведении

лучим более реальные параметры аппроксимации. В данном слу чае надо привлечь свое умение «читать» графики и (примерно, весьма примерно) определять параметры уравнения. Тем более, что выше мы уже определили для некоторых функций физическое значение входящих параметров. Это необходимо помнить при использовании современных математических пакетов: далеко не всегда предложенные («зашитые») в пакетах начальные прибли жения приводят к успешному решению, возможны сбои. И чтобы их не было, попробуйте использовать другие начальные прибли жения. Опора для их выбора – известные литературные данные, приближенное нахождение параметров из графиков и, наконец, Ваш личный опыт.

Теперь для приведенного примера решим три статистические задачи: оценки достоверности самого уравнения, его параметров и анализа полученных ошибок моделирования.

Прежде всего, значение F критерия весьма велико >2500 и достоверно при уровне значимости 0.000014. Конечно же, нуле вая гипотеза не верна, и мы с высокой степенью достоверности можем использовать полученное уравнение.

Весьма достоверны и параметры аппроксимации (см. таблицу II.3.6). Результаты, приведенные в таблице, определенно указы вают на то, что нулевая гипотеза отвергается в пользу альтерна тивной с уровнем значимости 0.0034 и 0.00025 соответственно, что явно ниже уровня значимости (α = 0.05), используемого в ес тественных науках.

292

Часть II. Применение математических моделей в почвоведении

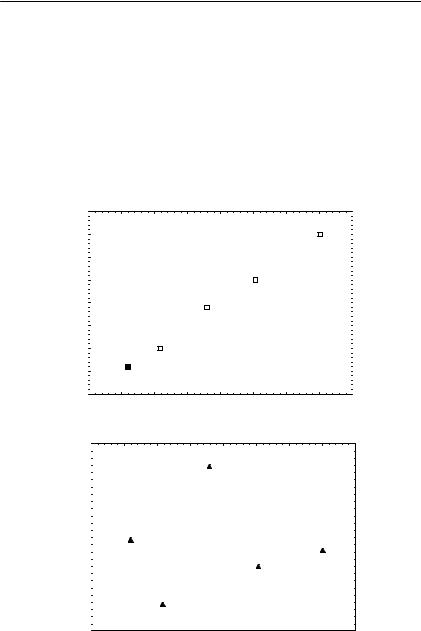
И последний шаг, который необходимо сделать для проверки модели: проанализировать ошибки аппроксимации и ответить на вопрос «Имеются ли систематические ошибки?». Для этого нужно построить графики и проанализировать две зависимости: зависи мости реальной переменной отклика от расчетной и ошибок ап проксимации от расчетной величины y. Ниже приведены графики этих зависимостей (рис. II.3.20).

Рис. II.3.20. Зависимости реальных величин от расчетных (а) и распреде ление погрешностей от расчетной величины глубины грунтовых вод (б)

293

Математическое моделирование в почвоведении

Оба эти графика указывают на достаточно хорошее совпаде ние расчетных и реальных величин, и на то, что ошибки не имеют систематического характера, не зависят от функции отклика, хотя и весьма велики. Действительно, график зависимости расчетной величины от реальной близок к линейному и представляет собой биссектрису угла начала координат, что указывает на отсутствие систематических ошибок. Второй график указывает, что ошибки не имеют систематического характера и не зависят от величины отклика y. Но графики определенно показывают, что для уверен ных утверждений необходимо получить еще немалое число экспе риментальныхданных.

При подборе параметров функции более сложного вида, чем степенная, расчеты будут усложняться, но алгоритмы вычислитель ных операций по сути остаются теми же. Так что описанная про цедура аппроксимации и последующего анализа параметров ос тается той же и будет включать указанные этапы, независимо от вида функции.

При подборе параметров к функциям более сложного вида, чем степенная, вид уравнения будет усложняться еще больше. Для нахождения значений параметров в таких уравнениях были адаптированы алгоритмы решения вычислительных задач в выс шей математике, которые можно разделить на методы детерми нистические и методы стохастические1.

Кроме метода наименьших квадратов существуют еще не сколько методов: не квадратичные функции потерь (когда ис пользуется вместо суммы наименьших квадратов сумма модулей отклонений и др.), метод взвешенных наименьших квадратов, метод максимума правдоподобия и др.

1 Стохастические методы, в отличии от детерминистических, основанных на точных и достоверных способах принятия решений, опираются на ста тистических совпадениях случайных величин по теории вероятности.

294

Часть II. Применение математических моделей в почвоведении

3.5.3. Детерминистические алгоритмы подбора параметров аппроксимации

Нередко используется (частности в пакете Statistica 6.0) алго ритм поиска значений параметров b1 и b2 по методу сканирова ния. Метод основан на переборе всех возможных значений пара метров b1 и b2 в поле значений [a0; an] так, чтобы a0 ≤ b1 ≤ an, a’0 ≤ b2 ≤ a’n с шагом µ (погрешность решения) и вычислением крите рия оптимальности Sr в каждой точке. Разновидностью метода является сканирование с переменным шагом.

Отличительным моментом данной группы алгоритмов явля ется то, что перебор осуществляется по заранее детерминирован ной траектории (при подборе одного параметра) или на поле зна чений (при подборе двух параметров).

Траектория, по которой осуществляется перебор значений (сканирование), может образовывать постоянное множество на всем поле значений параметров аппроксимации или уточняться при каждом последующем шаге (например, "перебор по нерав номерной сетке").

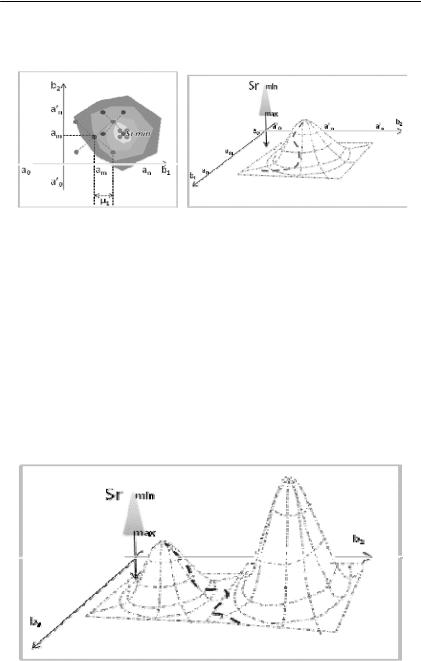
Сканирование с постоянным шагом (для случая подбора двух параметров) заключается в следующем. Строится поле значений (b1; b2). Далее исследуется одна из координатных осей (соответст вует значению одного из параметров от a0 до an) с шагом µ1. При этом значение второго параметра остается постоянным (рис. II.3.21). В каждой точке вычисляется значение критерия (средне квадратичной ошибки). Точность метода определяется частотой расположения выбранных точек на данной области изменения переменных. Когда весь диапазон изменения первого параметра исследован, значение второго параметра изменяется на величину µ2. Опять проводится вычисление критерия (среднеквадратичной ошибки) во всем диапазоне значений первого параметра с шагом

µ1.

295

Математическое моделирование в почвоведении

Рис. II.3.21. Графическое представление метода сканирования с посто янным шагом

Недостатком метода является огромное число вычислений, которое резко возрастает в зависимости от числа параметров в уравнении аппроксимации. Однако этот алгоритм позволяет оп ределить глобальный минимум на всем поле значений с точно стью, соответствующей шагу сканирования. В дальнейшем можно уточнить значения параметров с помощью алгоритма с перемен ным шагом.

Сканирование с переменным шагом отличается от вышеопи санного алгоритма тем, что осуществляется последовательное приближение заданных начальных значений параметров к иско мому оптимуму с минимальным среднеквадратическим отклоне нием. Расчет критерия (среднеквадратичной ошибки) осуществ ляется не на всем поле значений, что существенно сокращает время расчета. Пользователь аналитическим способом задает на чальные приближения – предварительные значения b1 (am) и b2 (a’m), где a0≤am≤an. Для этих значений вычисляется среднеквадра тическая ошибка Srm. Далее расчет Srm ведется для соседних с пер вой точкой координат b1 и b2, отличающихся от первоначальных значений на µ1: (am + µ1; a’m + µ1), (am – µ1; a’m – µ1), (am + µ1; a’m –

µ1), (am – µ1; a’m + µ1). Среди всех этих точек выбирается та, где значение Sr меньше. В следующем шаге (итерации) расчет коор динат будет происходить от нее, а шаг изменения координаты уменьшится на некоторую величину. В итоге расчет приведет к

296

Часть II. Применение математических моделей в почвоведении

минимальному значению Sr на координатном поле параметров и искомые b1 и b2 будут найдены (рис. II.3.22).

Рис. II.3.22. Графическое представление метода сканирования с пере менным шагом

Визуально алгоритм можно описать как поиск на неком «рельефе» самой глубокой точки, самой глубокой «ложбины», соответствующей минимальному значению критерия (средне квадратичной ошибки). Опасность данного метода состоит в том, что неверное задание начальных приближений может привести поиск минимального значения Sr к локальному понижению, «ложной ложбине» (рис. II.3.23).

Но оценка качества аппроксимации и значения параметров должны указать опытному исследователю на эту ошибку.

Рис. II.3.23. График метода сканирования с переменным шагом с ло кальным («ложным») понижением

297

Математическое моделирование в почвоведении

Разновидностью и усовершенствованием алгоритма сканиро вания являются метод Ньютона Гаусса и метод Левенберга Марквардта. Хотя есть и другие методы: квази ньютоновский ме тод, симплекс метод, метод Хука Дживиса, метод Розенброка, матрица Гессе. Есть более образно названные алгоритмы: гради ентный спуск, метод наикратчайшего спуска, спуск вдоль «овра га» — метод нахождения локального минимума (максимума) функции с помощью движения вдоль градиента, метод золотого сечения и др.

3.5.4. Стохастические алгоритмы подбора параметров аппроксимации

Метод Монте Карло – группа схожих алгоритмов, основан ных на случайном процессе подбора значений, генерации слу чайных чисел. При первой итерации значения параметров выби раются случайным образом в некотором пределе значений. При последующих итерациях значения коэффициентов уточняются. При этом новое значение искомого параметра уточняется за счет приращения также случайно выбранной величины. Если результат приращения не показал уменьшения критерия выбора (средне квадратичной ошибки или др.), то параметр возвращается к пре дыдущему значению и приращение вновь задается случайно. Та ким образом, на каждой итерации происходит уточнение всех ве совых коэффициентов. Процедура подбора параметров заканчи вается при нахождении минимального уровня критерия при оп ределенном количестве итераций.

Наглядной демонстрацией возможностей метода Монте Карло является интегрирование. Так, если необходимо посчитать интеграл от некоторой функции, то задача сводится к нахожде нию площади под графиком этой функции. Стандартный детер министический метод предполагает разбиение искомого отрезка функции на меньшие части, представляющие прямые отрезки, и подсчета площади под каждым из них. При сложных функциях расчеты могут занимать крайне продолжительное время.

298

Часть II. Применение математических моделей в почвоведении

В отличие от детерминистического метода, стохастический метод Монте Карло не зависит от пределов интегрирования функции и ее сложности. Алгоритм заключается в следующем. Ограничим в пределах интегрирования искомую функцию про стой фигурой, например, прямоугольником и рассчитаем его площадь. Далее будем случайным образом ставить точки внутри этого прямоугольника и подсчитывать, сколько из них попало часть прямоугольника под функцией, а сколько над ней (рис. II.3.24) Площадь фигуры под функцией будет составлять часть об щей площади прямоугольника в соответствии с долей попавших в нее точек. При условии большого числа точек метод Монте Карло оказывается достаточно точным даже для физических моделей.

y

x

Рис. II.3.24. Поиск наилучшего параметра методом Монте Карло

К вопросу о …. Что такое метод Монте Карло у ядерных физиков?

Вэпоху массовых открытий элементарных частиц, в 50 70

егоды прошлого столетия, физики в Дубне изучали появление новых частиц по их следам в различных трековых камерах, раз глядывая различные пленки с помощью микроскопов. Это время прошло. Современные ядерные физики, исследуя фундамен тальные основы материального мира, работают уже на со

299

Математическое моделирование в почвоведении

всем другом уровне, прежде всего, на уровне используемых энер гий. И на таких колоссальных ускорителях, когда происходит рождение большого количества новых частиц. Наблюдать их прямыми физическими методами не удается, просто невоз можно при столь огромном их количестве. И тогда физики ядерщики используют «метод Монте Карло». Смысл этого метода заключается в том, что берется так называемая Стандартная Модель, которая должна описывать рождение частиц при определенных уровнях энергии взаимодействия. Проигрывают на модели то или иное событие. Получают в ре зультате моделирования ответ, – когда и сколько частиц должно появиться, как они разлетаются и другие особенности их поведения. А затем сравнивают то, что получили в экспери менте на ускорителе с тем, что дают расчеты. Если резуль таты сходятся, значит теоретические построения верны, и они получили еще одно подтверждение их существования. На пример, в результате эксперимента получилось 20 частиц. А по расчетам – другие число, например, 17. По видимому, модель не учитывает процесса образования некоторого количества частиц, в нее должен быть введен дополнительный процесс, при котором образуются еще 3 частицы. Физически обоснован ная модель усовершенствуется, а мы начинаем глубже пони мать физические процессы, которые исследуем. Но вот почему у физиков ядерщиков этот метод получил жаргонное название «Монте Карло»? Название метода происходит от названия коммуны в княжестве Монако, широко известного своими мно гочисленными казино, поскольку именно рулетка является од ним из самых широко известных генераторов случайных чисел (на чем и основан метод). В моделировании почвенных процессов он называется методом адаптации и оптимизации. Но, в ко нечном счете, этот процесс сравнения экспериментальных и расчетных данных позволяет расширить, уточнить наше по нимание природы и дать начало новым знаниям.

300