17. Распределения молекул газа по направлениям движения в состоянии равновесия.

Рассмотрим газ, находящийся в состоянии равновесия. При этом он занимает объем V и содержит N молекул. При отсутствии внешних сил молекулы газа распределяются равномерно по объему V и движутся хаотически, не имея преимущественного направления. Если провести сферу радиусом R вокруг объема V и в произвольный момент времени продолжить направления скоростей движения всех молекул до пересечения с этой сферой, то вся сфера покроется точками в местах этих пересечений. Причем из-за отсутствия преимущественного направления в движении молекул (равновесие) поверхностная плотность этих точек  = N/4R² будет постоянна по всей сфере в любой момент времени.

Выберем на сфере произвольную элементарную площадку dS. Тогда количество точек, оказавшихся на этой площадке

dN = NdS /4R²= Nd/4, (1.3.1)

где d=dS/R² – телесный угол, под которым видна площадка из центра сферы. (Полный телесный угол, стягиваемый сферой

 = ∫ d = ∫ dS/R² =4R²/R²=4).

Соотношение (1.3.1) можно представить в виде

dN / N = d /4. (1.3.2)

Левая часть равенства (1.3.2) представляет собой отношение числа молекул dN, направления скоростей которых заключены в телесном угле d, к общему числу молекул и при большом N равна вероятности того, что взятая наугад молекула в газе имеет направление скорости, заключенное в телесном угле d. Формула (1.3.2) выражает закон равновероятности направлений движения молекул в равновесном состоянии газа^.

Р и с. 8

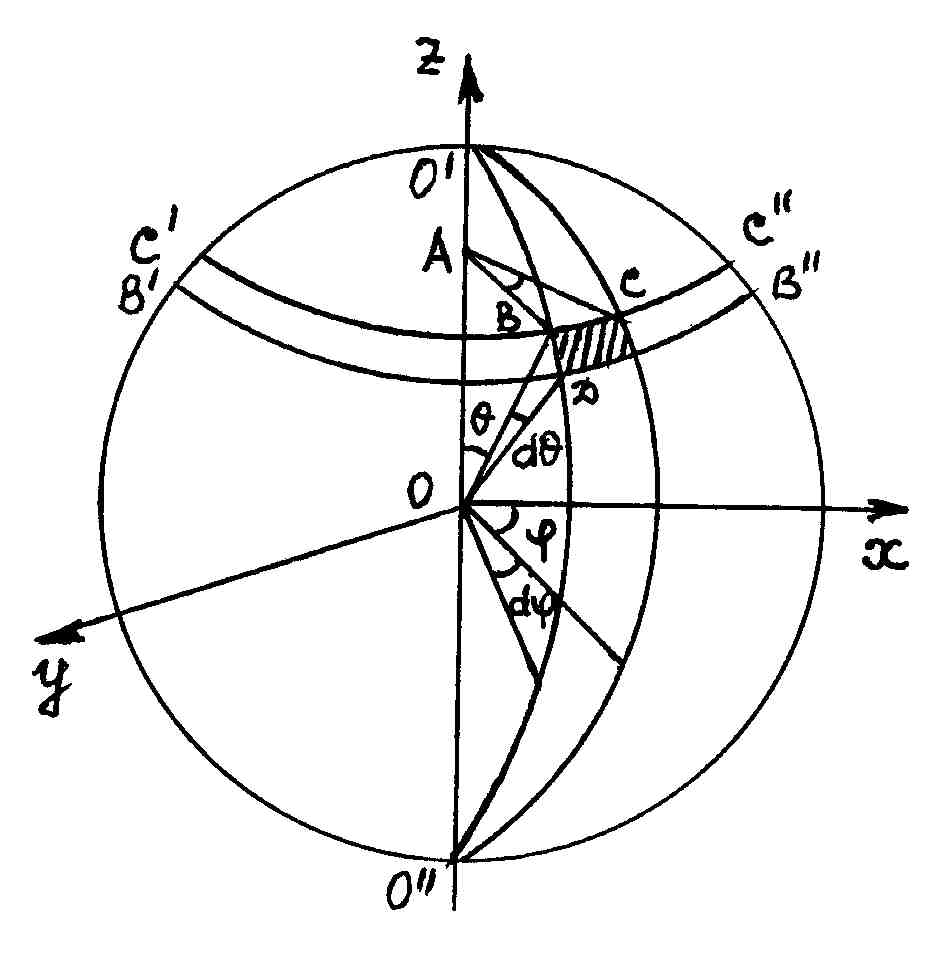
Найдем дифференциал площади dS в сферической системе координат. В результате пересечения четырех указанных окружностей получается элемент сферы, (на рис. 8 заштрихован) площадь которого

dS = BC·BD, (1.3.3)

где BC = ABd = R sin d, BD = R d.

Подставляя последние величины в формулу (1.3.3), получим выражение для бесконечно малой площади в сферической системе координат:

dS = R²sin d d. (1.3.4)

Из выражений (1.3.4) и (1.3.1) находим число частиц, которые имеют направления, определяемые сферическими углами, лежащими в интервалах от  до  + d и от  до  + d:

dN_, = N sin d d /4. (1.3.5)

18. Число ударов молекул о стенку сосуда (о единицу площади за единицу времени).

Объем цилиндра на рис. 9

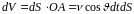, (1.4.1)

а число молекул в нем d = ndV, где n – концентрация молекул в сосуде.

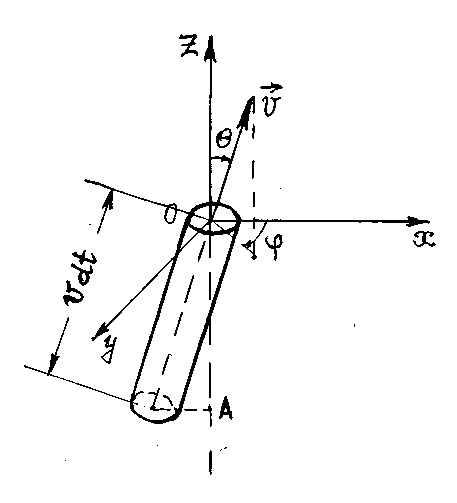
Р и с. 9

Обозначим через dn_ число молекул в единице объема газа, которые имеют скорости, заключенные в интервале (,  + d). Пусть среди этих молекул dn_ молекул в единице объема име­ют направления движения, определяемые сферическими углами, взяты­ми из интервалов (, + d) и (, + d). Количество таких молекул в единице объема газа равно

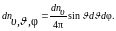(1.4.2)

Число же указанных молекул в объеме dV рассматриваемого цилинд­ра

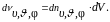(1.4.3)

С учетом формул (1.4.1) и (1.4.2) выражение (1.4.3) примет вид

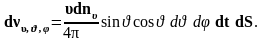(1.4.4)

Таким образом, среди всех молекул, находящихся в объеме dV цилиндра, d_,, молекул имеют близкие к  скорости, и их направления движения определяются углами, близкими к углам  и . Однако из объема V, занимаемого газом, к площадке dS подлетают молекулы с других направлений и с иными скоростями. Чтобы учесть это, необходимо проинтегрировать выражение (1.4.4) по всем возможным углам  и  и скоростям :

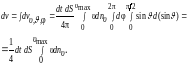(1.4.5)

Разделив обе части соотношения (1.4.5) на dtdS, получим

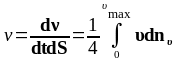(1.4.6)

Таким образом, выражение (1.4.6) определяет число ударов молекул га­за в единицу времени о единичную площадку стенки сосуда.

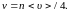(1.4.12)

Число ударов молекул газа в единицу времени о единичную площадку пропорционально концентрации и средней скорости их движения.