74. Кристаллические решетки. Решетки Браве. Элементы симметрии решетки. Классификация решеток Браве по кристаллографическим системам.

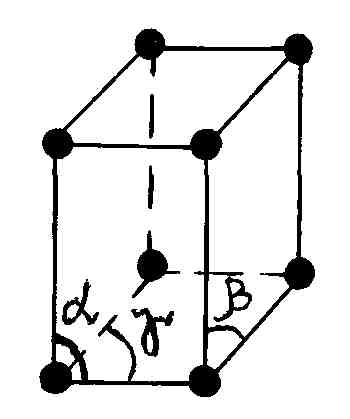
Упорядоченное расположение молекул в объеме кристалла можно получить, если рассматривать следующую сумму из трех векторов

(6.4.1)

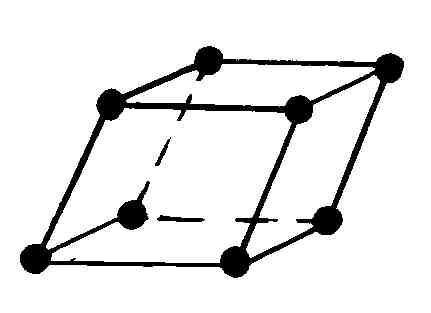
исходящих из точки, где расположена некоторая молекула (атом) кристалла, и расположенных под углами α, β, γ друг к другу, как показано на рис. 87.

Р и с. 87

Величины n₁, n₂, n₃ в векторной сумме (6.4.1) – целые числа, включая нуль. Если в конце вектора помещать молекулу при всевозможных значениях n₁, n₂, n₃, то таким образом мы получим так называемую кристаллическую решетку. Элементарная ячейка этой кристаллической решетки представляется параллелепипедом, построенным на трех векторах (на рис. 87 она выделена). Весь кристалл можно представить как смещение элементарных ячеек вдоль трех направлений . Модули этих векторов называют постоянными кристаллической решетки.

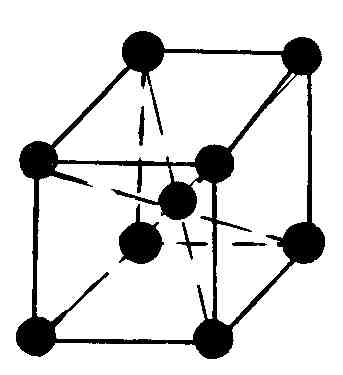
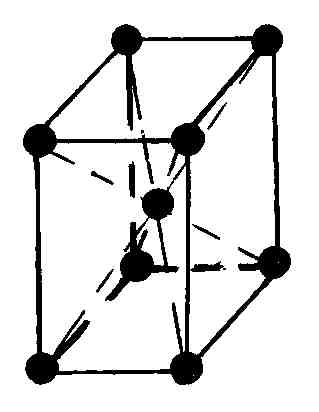
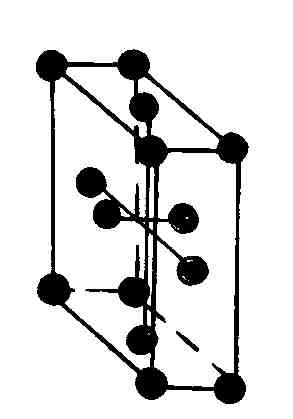
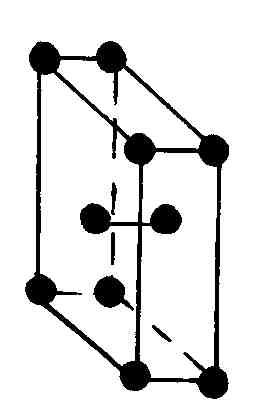
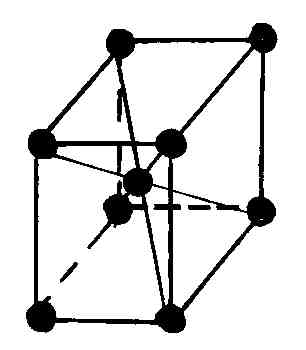
Многие реальные кристаллы представляются совокупностью нескольких кристаллических решеток, сдвинутых относительно друг друга (их называют подрешетками). Если в таких кристаллах выделить элементарную ячейку одной из подрешеток, то молекулы могут оказаться не только в вершинах ячейки, но и в центре ее граней и в центре ее диагональных плоскостей. В первом случае ячейки называются гранецентрированными или базоцентрированными, во втором – объемоцентрированными.

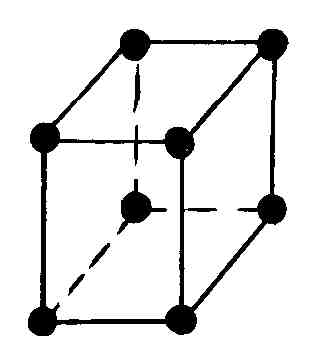
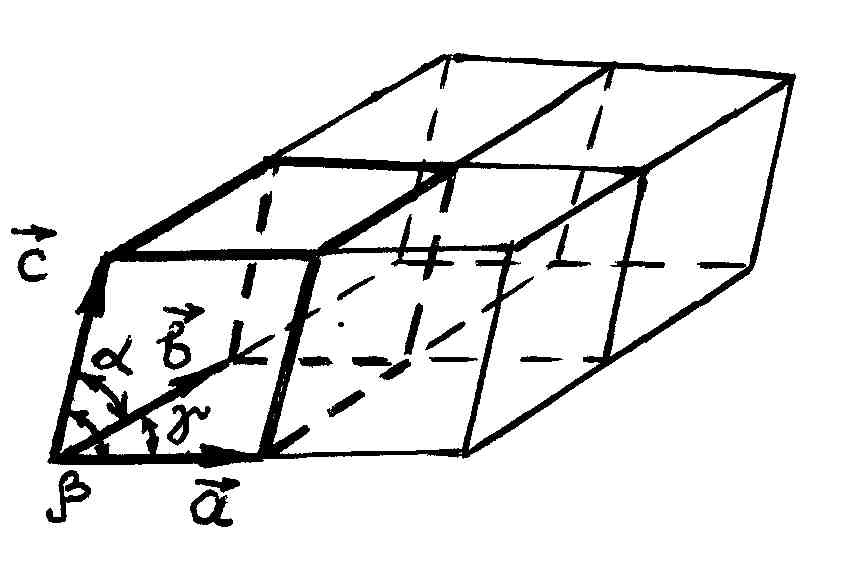
Как доказал А. Браве, существует всего четырнадцать трехмерных пространственных решеток (решеток Браве), подразделяющихся на семь систем (сингоний), в соответствии с семью различными типами элементарных ячеек (табл. 6.4.1).

Наиболее симметричной решеткой Браве является кубическая: симметрия куба сохраняется, если кроме частиц в вершинах кубов частицы будут находиться в их центрах или в центрах всех их граней (табл. 6.4.1).

Таблица 6.4.1

Кристаллические системы и решетки Браве

Кристалли- ческая система (сингония)	Ячейка, ее ребра и углы	Решетки Браве
		Простые (примитивные)	Сложные
			объемноцен-трированные	гранецент-рированные	базоцентри- рованные
Кубическая	куб a = b= c α = β = γ = = 90˚				─
Тетраго- нальная	Квадратная призма a = b ≠ c α = β = γ = = 90˚			─	─
Гексаго-нальная	Прямая при зма.В основан.правильный ромб a = b ≠ c α = β = 90˚ γ=120˚		─	─	─
Тригональная (ромбоэд- рическая)	Ромбоэдр a = b = c α = β= γ ≠ 90˚		─	─	─
Ромбиче-ская	Прямуголь ный парал- лелепипед a ≠ b ≠ c α = β = γ = 90˚
Монклин- ная	Прямая при зма. В основании правильный ромб a = b ≠ c α =  = 90˚≠ ≠ β			─	─
Триклин-ная	Косоуголь- ный парал- лелепипед a ≠ b ≠ c α ≠ β ≠ γ		─	─	─

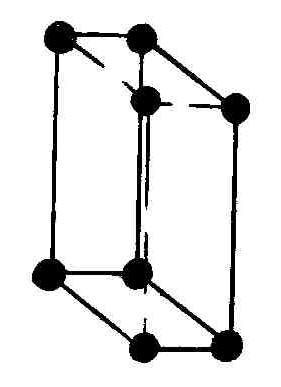
В тетрагональной системе простейшая решетка имеет вид правильной призмы с квадратом в основании. Вторая тетрагональная ячейка объемноцентрированная с дополнительным атомом в ее центре.

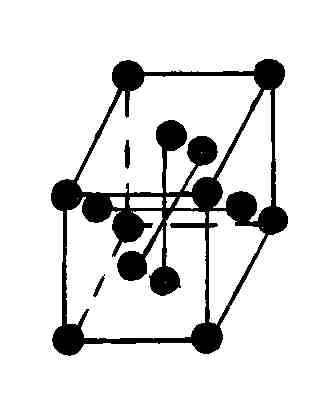
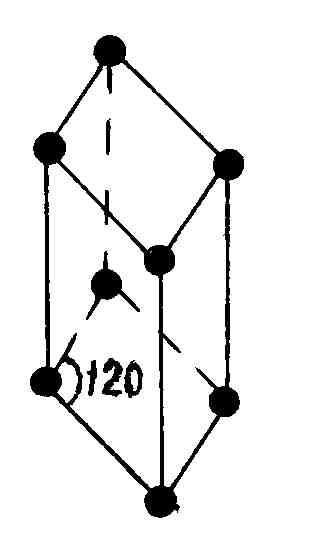
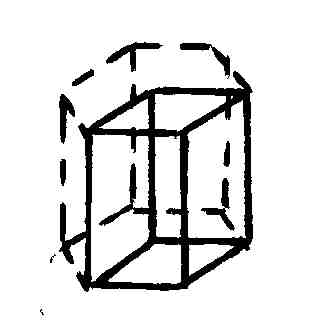
В гексагональной системе в качестве элементарной ячейки выбрана прямая призма, в основании которой лежит ромб с острым углом в 60°. Для того чтобы подчеркнуть пространственную симметрию гексагональных кристаллов, часто к элементарной ячейке добавляют еще две таких же ячейки, повернутые относительно друг друга на 120°, получая в результате правильную шестигранную призму (рис. 88). Из этих шестигранных призм строится гексагональный кристалл.

Р и с. 88

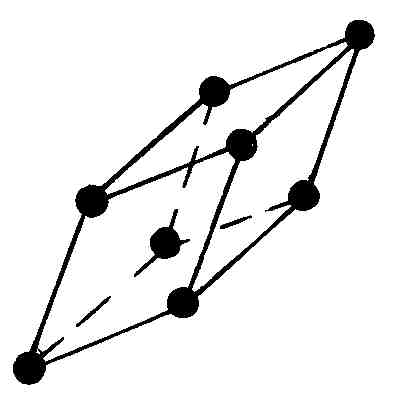
В тригональной (ромбоэдрической) системе параллелепипед Браве имеет форму ромбоэдра. Последний можно получить, равномерно растягивая куб в направлении его пространственной диагонали. Грани ромбоэдра – одинаковые ромбы.

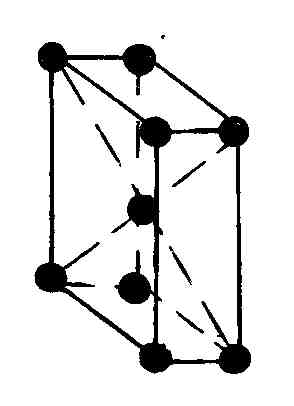
Элементарная решетка Браве в ромбической системе это прямоугольный параллелепипед. Имеется четыре типа ромбических решеток Браве: одна простая и три сложные; объемноцентрированная с дополнительным атомом в ее центре, гранецентрированная с четырьмя дополнительными атомами, расположенными в центре каждой из ее граней, и базоцентрированная с двумя дополнительными атомами в основаниях параллелепипеда.

В моноклинной системе элементарная ячейка это прямой параллелепипед, в основании которого расположен параллелограмм. В такой системе два типа решеток Браве: простая и объемноцентрированная.

Наконец, в триклинной системе параллелепипед Браве представляет собой косоугольный параллелепипед.

Среди кристаллических металлов в природе наибольшее распространение имеют гексогональная и кубическая структуры (табл. 6.4.2). При кристаллизации любых химических элементов природа отдает предпочтение объемноцентрированным и гранецентрированным структурам. Можно показать, что в этих структурах достигается минимум потенциальной энергии взаимодействия атомов, что обеспечивает их высокую устойчивость.

Таблица 6.4.2

Кристаллическая структура металлов

Li 3	Be 2
Na 3	Mg 2
K 3	Ca 1;2	Sc 1;2	Ti 2;3	V 3	Cr 3	Mn 1	Fe 1;3	Co 1;2	Ni 1;2	Cu 1	Zn 2
Rb 3	Sr 1	Y 2	Zr 2;3	Nb 3	Mo 2;3	Tc 2	Ru 1;2	Rh 1	Rd 1	Ag 1	Cd 2
Cs 3	Ba 3	La 1;2	Hf 2;3	Ta 3	W 3	Re 2	Os 1;2	Ir 1	Pt 1	Au 1	Hg 1

Обозначения: 1 – кубическая плотнейшая упаковка; 2 – гексаго-нальная плотнейшая упаковка; 3 – объемоцентрированная кубическая решетка.

Почти для всех металлов характерна максимально плотная упаковка частиц. Поясним два вида плотнейшей упаковки сферических частиц – кубическую и гексагональную.

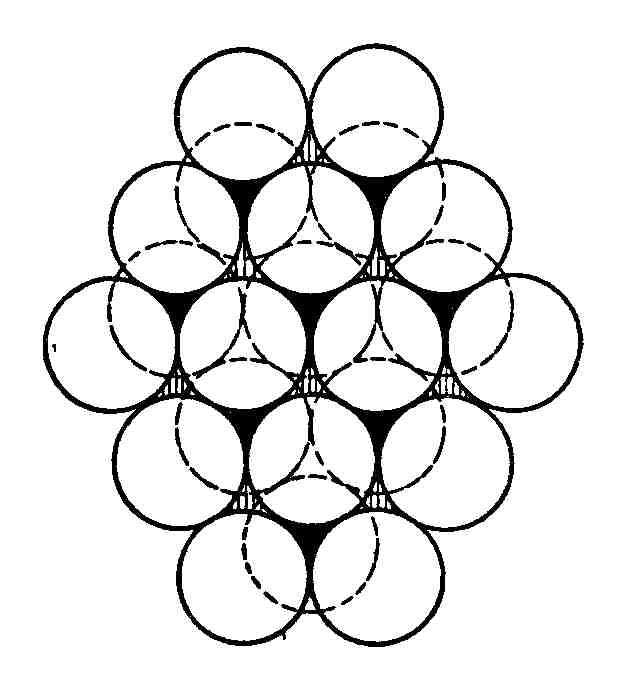
Пусть на плоскости уложен один слой шаров. Тогда наиболее плотным будет их расположение, показанное на рис. 89.

Р и с. 89

В этом случае каждый шар соприкасается с шестью другими. Для того чтобы расположить шары с двух сторон этого слоя с максимально плотной упаковкой, очевидно, шары верхнего и нижнего слоев следует располагать так, чтобы они попадали в лунки (углубления между шарами) среднего слоя. На рис. 89 изображены два слоя. Шары нижнего слоя показаны пунктиром, лунки, в которые они попадают, сделаны темными. Легко видеть, что в нижнем слое шаров половина лунок остается незанятыми шарами первого слоя (эти лунки заштрихованы). При уложении третьего слоя (сверху) возможны два варианта плотной упаковки: можно поместить шары или в темные лунки, или в заштрихованные; в первом случае мы получим гексагональную упаковку (рис. 90), во втором – кубическую гранецентрированную (рис. 91).

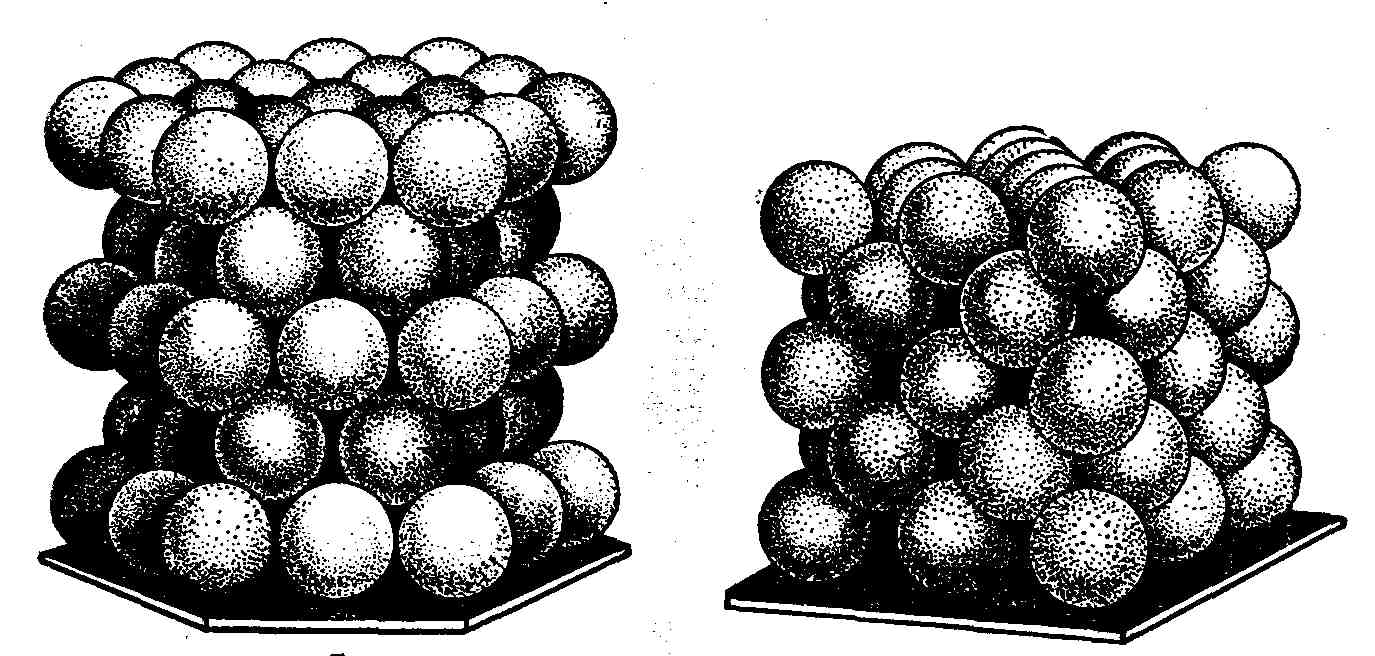
Р и с. 90 Р и с. 91 Р и с. 92

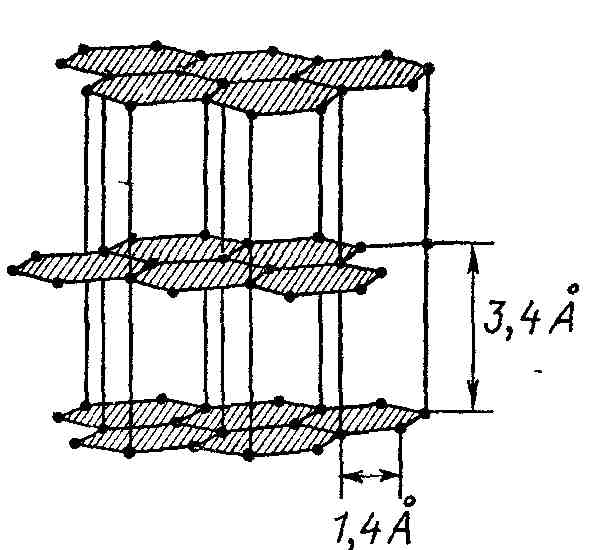
Примером кубической гранецентрированной плотнейшей упаковки ионов Na⁺ и Cl⁻ является хлорид натрия (соль), структура которого представлена на рис. 83. Интересен пример гексагональной решетки, имеющей слоистый характер. Это широко распространенная модификация углерода – графит (рис. 92).

Решетка состоит из плоских параллельных слоев, в которых атомы образуют правильные шестиугольники. Расстояние между слоями в несколько раз больше, чем расстояние между атомами внутри слоя, что объясняет легкость, с которой отделяются слои графита друг от друга.

?75. Кристаллографические системы координат. Обозначение атомных плоскостей и направлений в кристаллах.

?76. Дефекты в кристаллах. Точечные дефекты. Дислокации.

Дефектами кристалла называют всякое нарушение трансляционной симметрии кристалла — идеальной периодичности кристаллической решётки. Различают несколько видов дефектов по размерности. А именно, бывают нульмерные (точечные), одномерные (линейные), двумерные (плоские) и трёхмерные (объемные) дефекты.