69. Капиллярные явления.

Поместим цилиндрическую трубку малого сечения (капилляр) одним концом в жидкость, налитую в широкий сосуд (рис. 76).

Если жидкость частично смачивает капилляр, то ее поверхность в капилляре будет вогнутой сферической формы (рис. 76, а). При этом жидкость в капилляре поднимется на некоторую высоту h. Это можно объяснить тем, что давление на плоской поверхности жидкости, равное сумме атмосферного давления p₀ и молекулярного давления p_М больше, чем давление p₀+p_М–2s/R на вогнутой поверхности мениска на величину давления Лапласа. Вследствие этой разности давлений жидкость в капилляре поднимется до такого уровня h, при котором гидростатическое давление столба жидкости rgh уравновесится давлением Лапласа p_Л=2s/R, где R – радиус сферы мениска, т. е.

.

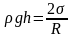Откуда

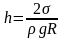. (5.5.1)

Как видно из рис. 76 радиус кривизны мениска R связан с радиусом капилляра r равенством R = r/cosq, где q – краевой угол. Учтя это, перепишем (5.5.1) в виде

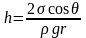. (5.5.2)

Если жидкость полностью смачивает твердое тело капилляра (к примеру, вода - чистое стекло), то q = 0 и

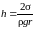. (5.5.3)

В этом случае сферическая поверхность мениска вписана во внутреннюю поверхность цилиндрического капилляра (R = r).

Если же жидкость частично не смачивает капилляр (рис.76, б), то давление на плоской поверхности жидкости, равное p₀ + p_М, будет меньше, чем давление p₀ +p_М=2s /R на выпуклой поверхности мениска, в результате чего жидкость в капилляре опустится на величину h, определяемую формулой (5.5.2). При этом h < 0, так как при частичном несмачивании краевой угол p/2 £ q £ p и cosq <0.

70. Давление насыщенного пара над искривленной поверхностью жидкости.

Предположим, что в закрытом сосуде имеется насыщенный пар и жидкость, в которую погружены два капилляра, один смачиваемый, другой – несмачиваемый этой жидкостью (рис. 77).

Давление насыщенного пара уменьшается с высотой по барометриче-

ской формуле (1.13.20) и на высоте h будет равно

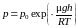, (5.6.1)

где p₀ – давление пара на плоской поверхности жидкости, h – вы­сота жидкости в капилляре.

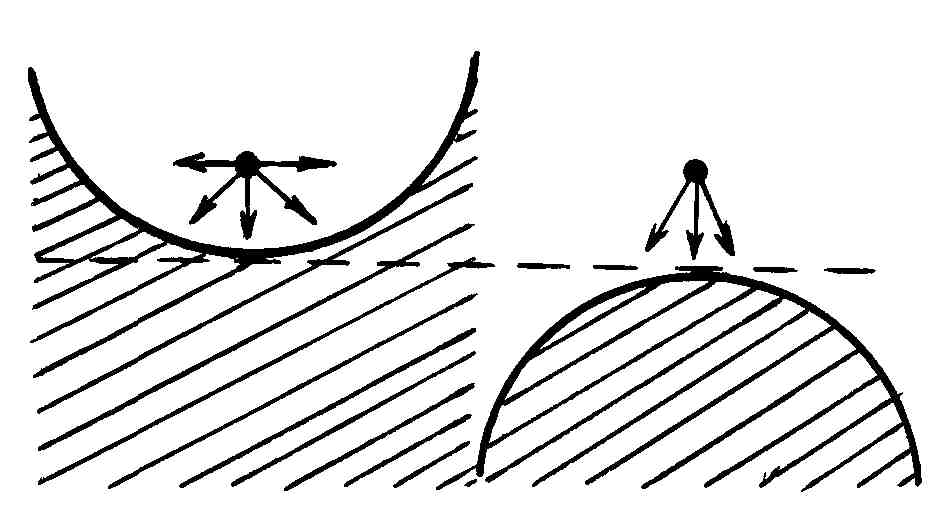
Р и с. 77

Легко видеть, что при обычных температурах величина 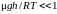. Поэтому экспоненту можно разложить в ряд по степеням этой величины: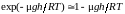 . В результате выражение (5.6.1) примет вид:

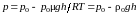, (5.6.2)

где ρ₀ – плотность насыщенного пара. Подставляя в формулу (5.6.2) выражение (5.5.1), получим величину давления пара над вогнутой поверхностью мениска (h > 0):

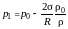, (5.6.3)

где ρ – плотность жидкости. Следовательно, давление р₁ пара над вогнутой поверхностью жидкости меньше давления пара над плоской на величину 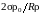, зависящую от радиуса R кривизны этой поверхности.

Если жидкость частично не смачивает капилляр (h < 0), то давление р₂ пара над выпуклой поверхностью мениска будет больше давления пара над плоской:

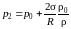. (5.6.4)

Существенно отметить, что разность давлений насыщенных паров над плоской и кривой поверхностью жидкости определяется только радиусом кривизны R и параметрами (σ, ρ) жидкости и пара (ρ₀) и не зависит от силы тяжести (g) и высоты h, на которой расположена кривая поверхность жидкости.

Физически различие между давлением насыщенного пара над плоской и искривленной поверхностями жидкости объясняется следующим образом. Равновесие между насыщенным паром и жидкостью означает равенство между числами молекул, ежесекундно переходящих из жидкости в пар и обратно. При вогнутой поверхности переходу молекул из жидкости в пар препятствует большое число соседних (находящихся поблизости) молекул, чем при плоской поверхности (рис. 77), поэтому при данной температуре ежесекундное число молекул, которые могли бы преодолеть притяжение к поверхностному слою жидкости и перейти в пар, меньше, чем в случае плоской по­верхности, что создает меньшее давление паров над вогнутой поверхностью. Наоборот, переход молекул с выпуклой поверхности жидкости в пар потребует меньшей затраты энергии, так как число близко расположенных молекул, препятствующих этому переходу, будет меньше, чем при плоской поверхности (рис. 77); следовательно, число молекул, ежесекундно покидающих выпуклую поверхность, будет при одинаковой температуре больше, чем аналогичное число молекул для плоской поверхности. В результате над выпуклой поверхностью жидкости будет создано большее давление паров, чем над плоской.

Предположим, что над плоской поверхностью жидкости в атмосфере ее пара находятся капельки этой жидкости. Так как пар является насыщенным для плоской поверхности, т. е. имеет давление р₀, то для капелек с выпуклой поверхностью этот же пар оказывается ненасыщенным, так как, согласно (5.6.4), выпуклые поверхности находятся в равновесии с паром большего давления, чем плоские поверхности. Вследствие этого капельки жидкости испаряются. Если же в атмосфере имеются капельки различных радиусов, и если давление паров в атмосфере больше, чем давление пара над каплей самого малого размера, то этот пар будет пересыщенным для всех капелек, и на них начнется процесс конденсации, который приведет к увеличению размеров всех капелек, и они, в конце концов, выпадут в виде дождя.

?71. Испарение жидкостей. Скрытая теплота испарения. Температурная зависимость давления насыщенных паров. Уравнение Клапейрона-Клаузиуса.