54. Внутренняя энергия газа Ван-дер-Ваальса. Адиабатическое расширения газа ВдВ в пустоту.

Выражение для внутренней энергии газа Ван-дер-Ваальса найдем следующим образом. При расширении газа его молекулы совершают работу против сил молекулярного давления . Эта работа равна

, (3.7.1)

где – объем одного моля газа.

С другой стороны, эта работа идет на увеличение потенциальной энергии взаимодействия молекул:

. (3.7.2)

Из выражений (3.7.1–3.7.2) следует, что

. (3.7.3)

Интегрирование этого выражения дает

. (3.7.4)

Внутренняя энергия газа состоит из кинетической и потенциальной энергий, т. е.

. (3.7.5)

Подставим выражение (3.7.4) в (3.7.5).

. (3.7.6)

При газ становится идеальным и его внутренняя энергия равна кинетической энергии движения молекул и равна, как мы знаем, , т. е.

. (3.7.7)

С другой стороны, при из (3.7.6)

. (3.7.8)

Из сравнения выражений (3.7.7) и (3.7.8), заключаем, что . Таким образом, из (3.7.6)

. (3.7.9)

Внутренняя энергия молей газа

, (3.7.10)

где V – объем, занимаемый молями газа.

Рассмотрим изотермическое расширение газа Ван-дер-Ваальса от объема до объема . Изменение внутренней энергии на основании (3.7.10)

. (3.7.11)

Поэтому, согласно первому закону термодинамики, работа, произведенная газом Ван-дер-Ваальса при изотермическом расширении,

т. е. меньше количества полученного тепла, тогда как для идеального газа эта работа в точности равнялась количеству приобретенного тепла. Это объясняется тем, что в реальном газе при его изотермическом расширении часть тепла идет на работу против сил притяжения между молекулами, т. е. на увеличение потенциальной энергии молекул.

Рассмотрим далее адиабатное расширение газа Ван-дер-Ваальса без совершения внешней работы (так называемое расширение газа в вакуум). В этом случае в первом законе термодинамики необходимо положить и Тогда и т. е.

,

и, учитывая выражение (3.7.10), последнее равенство можем переписать в виде:

.

Откуда находим

,

так как . Таким образом, газ Ван-дер-Ваальса при расширении в вакуум охлаждается. Охлаждение происходит потому, что в этом процессе часть кинетической энергии газа тратится на работу против сил притяжения между молекулами.

55. Эффект Джоуля-Томсона. Общая термодинамическая теория дифференциального эффекта Джоуля-Томсона.

Опыт показывает, если на пути потока газа или жидкости, текущего по некоторому каналу, встречается препятствие, сужение поперечного сечения потока, а затем сечение потока увеличивается, то давление протекающего газа (жидкости) за препятствием всегда оказывается меньшим, чем перед ним. Так, например, этот эффект наблюдается при движении воды через не полностью открытый водопроводный кран или при движении воздуха через не полностью открытую задвижку в дымоходах печей.

Эффект падения давления потока рабочего вещества в процессе протекания через препятствие (сужение) в канале называют дросселированием, а само препятствие – дросселем. Физически падение давления за местным сопротивлением обусловлено рассеянием энергии потока, расходуемой на преодоление этого местного сопротивления(трение).

Эффектом Джоуля – Томсона называется изменение температуры газа при его адиабатном протекании через дроссель.В опытах Джоуля – Томсона использовалась адиабатно изолированная цилиндрическая трубка с находящимся внутри нее дросселем, изготовленным из ваты или очесов шелка, плотно сбитых в пробку (рис. 54).

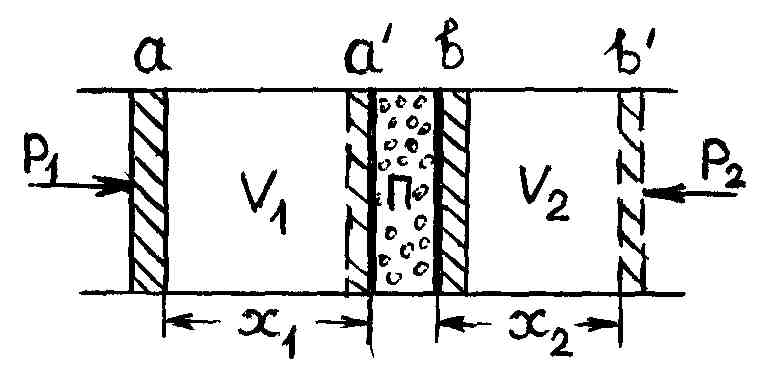
Р и с. 54

Вследствие трения, при медленном проталкивании газа через пробку, газ и пробка обмениваются между собой теплотой. Из-за наличия препятствия скорость потока до и после препятствия пренебрежимо мала, что позволяет пренебречь кинетической энергией потока.

В результате опытов Джоуль и Томсон установили, что все газы, за исключением водорода (и гелия, как выяснилось впоследствии), при дросселировании охлаждаются.

На современных установках, использующих эффект Джоуля – Томсона, это охлаждение достигает весьма больших значений. Например, при адиабатном дросселировании водяного пара от давления 300 атм. и температуры 450 С до давления 1 атм. температура пара уменьшается до 180 С (т. е. на 270 С!), а воздух, испытывая дроссель-эффект от комнатной температуры и давления 200 атм. до давления 1 атм., охлаждается примерно на 40 С.

Рассмотрим термодинамическую теорию эффекта Джоуля – Томсона.

Пусть в исходном состоянии газ занимает объем между поршнем a и дросселем , второй поршень вплотную примыкает к дросселю (рис. 54). Станем медленно вдвигать поршень a, сохраняя давления и , действующие на поршни, постоянными. (Технически постоянство давлений обеспечивается компрессорами). Газ, просачиваясь с малой скоростью через дроссель, заполнит объем и будет находиться под давлением .

Работа, совершаемая над газом слева от дросселя,

. (3.8.1)

Совершаемая же газом работа против внешнего давления равна

. (3.8.2)

Общая работа, произведенная в процессе Джоуля – Томсона,

. (3.8.3)

По первому закону термодинамики, работа, производимая в адиабатном процессе, равна убыли внутренней энергии, т. е.

.

Откуда

или

. (3.8.4)

Таким образом, в результате адиабатного дросселирования значение энтальпии рабочего вещества до дросселя и после него одинаковы.

Для характеристики степени охлаждения рабочего вещества при адиабатном дросселировании вводится так называемый коэффициент Джоуля – Томсона

. (3.8.5)

Зная коэффициент , можно найти изменение температуры в дроссель-эффекте при конечном значении разности давлений:

, (3.8.6)

где и – температуры рабочего вещества перед дросселем и за ним соответственно.

Так как в дроссель-эффекте всегда , то коэффициент Джоуля – Томсона , если и газ, таким образом, охлаждается (положительный эффект Джоуля – Томсона); если же (газ нагревается), то (отрицательный эффект Джоуля – Томсона).

Применив первый и второй законы термодинамики, найдем общее выражение для коэффициента Джоуля – Томсона. Так как в дроссель-эффекте , то

. (3.8.7)

Будем рассматривать энтальпию как функцию температуры и давления. Поэтому

. (3.8.8)

Из последнего равенства находим

. (3.8.9)

Используя соотношение (2.7.14), равенство (3.6.9) можем записать в виде (расчеты будем вести для одного моля вещества):

. (3.8.10)

Производную найдем через легко измеримые величины. Для этого в основном уравнении термодинамики (2.14.3) выразим внутреннюю энергию через энтальпию:

. (3.8.11)

Подставив выражение (3.8.8) в (3.8.11), будем иметь

. (3.8.12)

Рассматривая энтропию как функцию температуры и давления , можем записать:

. (3.8.13)

Сравнивая выражения (3.8.12) и (3.8.13), получаем

; .

Первое из этих равенств продифференцируем по при постоянном , а второе – по при постоянном и учитывая, что получим

Откуда находим

. (3.8.14)

Подставим выражение (3.8.14) в (3.8.10). В результате получим общее термодинамическое соотношение для коэффициента Джоуля – Томсона:

. (3.8.15)

Если газ идеальный, то и , т. е. в процессе адиабатного дросселирования температура идеального газа не изменяется. Это один из характерных признаков идеального газа.