5. Агрегатные состояния вещества. Характер теплового движения в этих состояниях. Особенности теплового движения в различных агрегатных состояниях вещества.

Одним из важнейших параметров, ха­рактеризующих молекулу, является минимальная потенциальная энер­гия взаимодействия 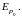Силы притяжения, действующие между молекулами стремятся сконденсировать вещество, т. е. сблизить его молекулы до расстояния r₀, когда их потенциальная энер­гия взаимодействия минимальна и равна 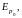но этому сближению препятствует хаотическое тепловое движение молекул. Интенсивность этого движения определяется средней кинетической энергией моле­кулы, которая имеет порядок kT, где k – постоянная Больцмана. 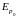Агрегатные состояния вещества существенным образом зависят от соотношения величин и kT.

Предположим, что температура рассматриваемой системы молекул столь высока, что

kT >> В этом случае интенсивное хаотическое тепловое движение мешает силам притяжения соединить мо­лекулы в агрегаты из нескольких частиц, сблизившихся до расстояния r₀: при соударениях большая кинетическая энергия молекул будет легко разбивать эти агрегаты на составляющие молекулы и, таким образом, вероятность образования устойчивых агрегатов будет как угодно малой. В этих обстоятельствах рассматриваемые молекулы, очевидно, будут находиться в газообразном состоянии.

Если температура системы частиц очень низкая, т. е. kT << молекулам, действующими силами притяжения, тепловое движение не может помешать приблизиться друг к другу на расстояние близкое к r₀ в определенном порядке. При этом система частиц будет находить­ся в твердом состоянии, а небольшая кинетическая энергия теплового движения вынудить молекулы совершать беспорядочные малые ко­лебания около определенных положений равновесия (узлов кристал­лической решетки).

Наконец, при температуре системы частиц, определяемой из приближенного равенства kT ≈ кинетическая энергия тепло­вого движения молекул, величина которой примерно равна потенциаль­ной энергии притяжения, не сможет переместить молекулу на расстоя­ние, существенно превышающее r₀. В этих условиях вещество будет находиться в жидком агрегатном состоянии.

Таким образом, вещество, в зависимости от своей температуры и величины присущей данному сорту составляющих его молекул, будет находиться в газообразном, твердом или жидком состоянии.

При нормальных условиях расстояние между молекулами в газе в десятки раз (см. пример 1.1) превышают их размеры; большую часть времени они движутся прямолинейно без взаимодей­ствия и только значительно меньшую часть времени, когда находят­ся на близких расстояниях от других молекул, взаимодействуют с ними, меняя направление своего движения. Таким образом, в газо­образном состоянии движение молекулы выглядит так, как схематич­но показано на рис.7, а.

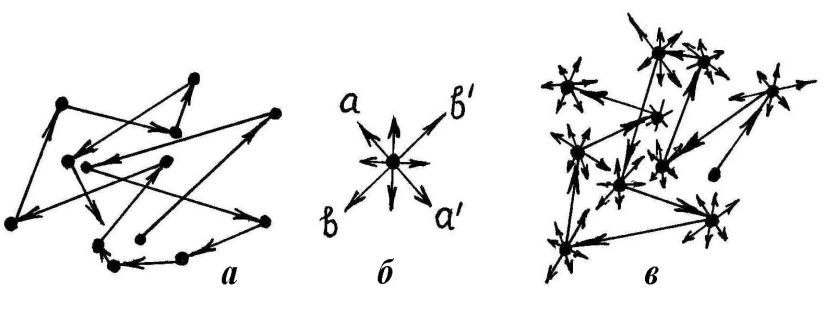
В твердом состоянии каждая молекула (атом) вещества находит­ся в равновесном положении (узел кристаллической решетки), возле которого она совершает малые колебания, причем направление (к при­меру, аа' на рис. 7, б) и амплитуда этих колебаний случайно изменяются (к примеру, на направление bb') через время, значительно большее периода этих колебаний; частоты колебаний молекул в общем случае неодинаковы. Колебания отдельной молекулы твердого тела в общих чертах представ­лена на рис. 7, б.

Молекулы твердого тела упакованы так плотно, что расстояние между ними примерно равно их диаметру, т.е. расстоянию r₀ на рис. 3. Известно, что плотность жидкого состояния примерно на 10 % меньше плотности твердого, при прочих равных условиях. Поэтому расстояние между молекулами жидкого состояния нес­колько больше r₀. Учитывая, что в жидком состоянии молекулы об­ладают еще и большей кинетической энергией теплового движения, следует ожидать, что, в отличие от твердого состояния, они могут, совершая колебательное движение, достаточно легко менять свое местоположение, перемещаясь на расстояние, существенно не превышаю­щее диаметр молекулы. Траектория движения молекулы жидкости приблизительно выглядит так, как схематически показано на рис. 7, в. Таким образом, движение молекулы в жидкости сочетает в себе посту­пательное движение, как это имеет место в газе, с колебательным, что наблюдается в твердом теле.

Несмотря на неодинаковый характер движения молекул в различ­ных агрегатных состояниях, общим является случайность, непредска­зуемость этих движений. Средняя кинетическая энергия этих беспоря­дочных движений определяет тепловое состояние вещества, его темпе­ратуру.