52. Уравнение Ван-дер-Ваальса – Уравнение состояния неидеальных газов. Опытное определение констант уравнения Ван-дер-Ваальса.

Как отмечалось ранее, при низких температурах и высоких давлениях уравнение Менделеева – Клапейрона для одного моля вещества

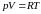(3.4.1)

дает существенные отклонения от значений, измеряемых на опыте.

Были сделаны многочисленные попытки найти уравнение состояния для реального вещества, которое могло бы охватить, если не все состояния вещества, то хотя бы газообразное и жидкое. Из множества предложенных уравнений наибольшей известностью пользуется уравнение Ван-дер-Ваальса:

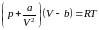, (3.4.2)

записанное для одного моля вещества. Для молей это уравнение имеет вид:

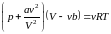. (3.4.3)

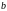Постоянные и определяются экспериментально и имеют различные значения для разного сорта молекул. Уравнение (3.4.2) не выводится, оно устанавливается введением в уже известное уравнение Менделеева – Клапейрона двух поправок. Чтобы обосновать их введение заметим, что в уравнении (3.4.2) объем 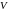означает объем сосуда, в котором содержится один моль газа. В случае идеального газа, состоящего из материальных точек, весь этот объем доступен для движения молекул. В реальном газе сами молекулы занимают некоторую часть объема сосуда, и эта часть недоступна для всех других молекул. Эту часть объема следует вычесть из объема . Тогда уравнение (3.4.2) приобретет вид

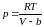. (3.4.4)

Из последнего выражения видно, что поправка равна тому объему, который занимал бы газ при бесконечно большом давлении, т. е. молекулы реального газа не могут сблизиться друг с другом до расстояния равного нулю, даже при бесконечно большом давлении. Поэтому введение поправки означает приблизительный учет сил отталкивания между молекулами.

Как мы знаем, между молекулами действуют не только силы отталкивания, но и силы притяжения. Любая молекула, расположенная вблизи стенки сосуда 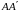испытывает результирующую силу притяжения

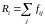(3.4.5)

со стороны молекул, расположенных в сфере действия сил притяжения 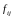(рис. 51).

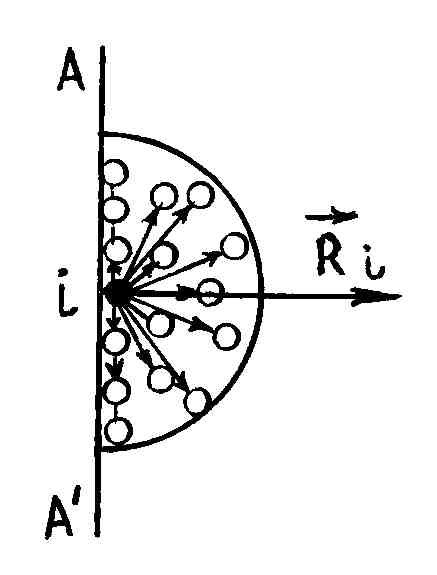
Р и с. 51

На поверхности стенки выберем площадку . Пусть на ней оказалось молекул. Тогда результирующая сила, действующая на молекулы этой площадки со стороны газа

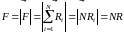, (3.4.6)

так как из условий симметрии все силы 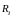имеют одинаковую величину и направление. Если силу 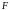разделить на площадь , получим так называемое молекулярное давление 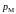, с которым молекулы, находящиеся у стенки, действуют на остальную массу газа:

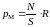. (3.4.7)

Каждый из сомножителей в формуле (3.4.7), очевидно, пропорционален плотности 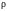газа, которая, в свою очередь, обратно пропорциональна объему газа, поэтому можно записать:

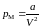, (3.4.8)

где a – положительный постоянный коэффициент.

Таким образом, в результате действия сил притяжения давление на стенку со стороны газа будет меньше, по сравнению с тем давлением (3.4.4), которое испытала бы стенка, если бы сил притяжения между молекулами не было, т. е.

.

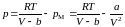Откуда находим уравнение Ван-дер-Ваальса:

. (3.4.9)

Поясним появление в формуле (3.4.9) добавочного давления. Пусть газ находится в цилиндре под невесомым поршнем. Внешнее давление стремится сжать газ, т. е. сблизить его молекулы. Если бы молекулы газа друг друга не притягивали, газ испытывал бы на себе одно только внешнее давление . Но взаимное притяжение молекул, как мы выяснили, также стремится приблизить молекулы друг к другу, т. е. действует в том же направлении, как и внешнее давление . Поэтому результат притяжения молекул сказывается в кажущемся увеличении внешнего давления на газ, как будто бы к величине давления на поршень прибавилось некоторое добавочное давление .

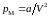Опытное определение констант уравнения Ван-дер-Ваальса

Для опытного определения постоянных a и исследуемый газ помещаем в закрытый сосуд объема со встроенным манометром и измеряют давление этого газа при различных температурах. Численным дифференцированием полученной на опыте кривой 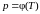определяем частную произво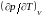дную . Из уравнения Ван-дер-Ваальса находим эту производную

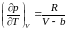. (3.5.1)

Отсюда получаем величину :

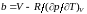. (3.5.2)

Подставляя выражение (3.5.2) в уравнение Ван-дер-Ваальса (3.4.9), вычисляем другую величину a:

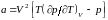. (3.5.3)

Опыт показал, что величины a и не являются константами, а зависят от температуры, хотя и слабо. В расчетах, использующих уравнение Ван-дер-Ваальса, в качестве констант a и берут средние значения функци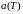й и 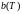в интересующем интервале температур

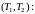
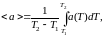
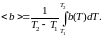
?53. Изотермы уравнения Ван-дер-Ваальса и их сравнение с экспериментальными изотермами. Определение критических параметров вещества из уравнения ВдВ. Метастабильные состояния вещества – пересыщенный пар и перегретая жидкость. Камера Вильсона и пузырьковая камера.

На рис. 52 представлены изотермы газа Ван-дер-Ваальса.

При очень высоких температурах они имеют форму, близкую к гиперболам ; эти изотермы характеризуют газообразное состояние вещества (почти идеальный газ). По мере уменьшения температуры форма изотермы изменяется и при некоторой температуре 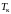(критическая) обнаруживает точку перегиба кривой. При еще меньших температурах (докритических) изотермы вместо горизонтального участка, соответствующего фазовому переходу жидкость – пар, имеют волнообразный участок 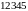(рис. 53).

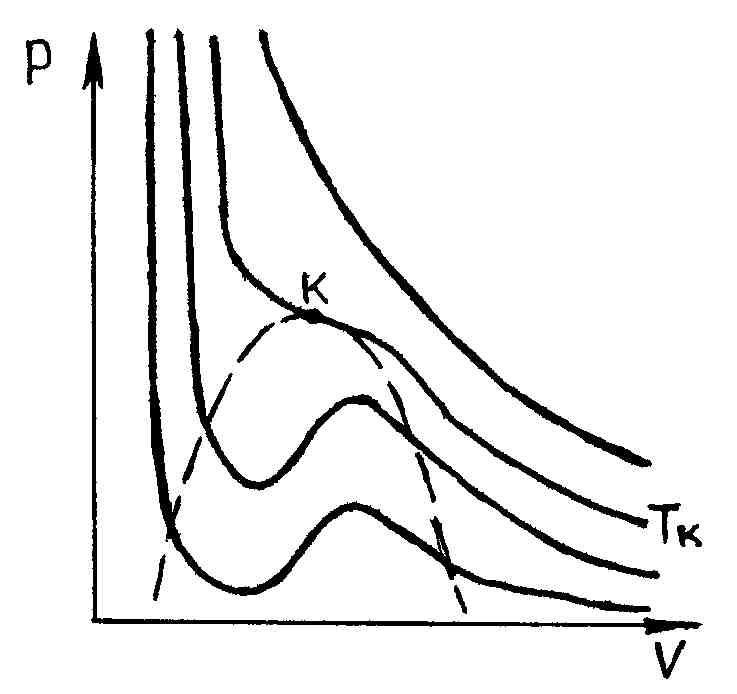
Р и с. 52 Р и с. 53

Измерения показывают, что изотермы реального вещества практически совпадают с изотермой Ван-дер-Ваальса на участках 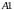(газообразное состояние) и 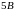(жидкое состояние). Однако в средней части вместо горизонтального участка 51, соответствующего фазовому переходу жидкость – пар, изотерма Ван-дер-Ваальса имеет волнообразный участок . Этот волнообразный участок характеризуется следующим образом. Участок 12 соответствует метастабильному состоянию пара (пересыщенный пар), а участок 54 – метастабильному состоянию жидкости (перегретая жидкость). В точке 1 имеется только насыщенный пар, а в точке 5 – только кипящая жидкость. Что касается участка 234 волнообразной кривой, то он физически неосуществим, так как в природе нет веществ, для которых при постоянной температуре увеличение объема приводило бы к росту давления. Последнее возможно только в случае, если на этом участке температура не является постоянной. Пересыщенный пар (участок 12) – газообразное состояние вещества, в котором давление p больше, чем давление насыщенного пара при данной температуре – можно на опыте получить, сжимая чистый газ до давления, большего давления насыщенных паров, и он не будет конденсироваться. Состояние пересыщенного пара, хотя и обладает определенной устойчивостью, но оно менее устойчиво, чем двухфазное состояние (изобара 135), при котором, как мы знаем, часть вещества находится в виде жидкости, а часть – в виде насыщенного пара. Поэтому при небольшом внешнем воздействии пересыщенный пар частично переходит в жидкость, а оставшийся пар становится насыщенным.

Перегретую жидкость (участок 45) – состояние, характеризующееся тем, что оно существует при давлении более низком, чем давление насыщенного пара при данной температуре – можно получить при длительном кипячении чистой жидкости, в результате чего из жидкости удаляются газовые пузырьки (центры парообразования), и жидкость нагревается до температуры выше температуры кипения при данном давлении. Состояние перегретой жидкости также оказывается менее устойчивым, чем состояние равновесия между жидкостью и насыщенным паром. Если в такую перегретую жидкость ввести частицы постороннего вещества, то совершается быстрый переход ее в двухфазное состояние.

Состояния пересыщенного пара и перегретой жидкости используются в приборах ядерной физики (камера Вильсона и пузырьковая камера) для регистрации и измерения параметров элементарных частиц.

Если на изотерме Ван-дер-Ваальса волнообразный участок заменить некоторой горизонтальной прямой 135, то полученная так изотерма будет качественно правильно описывать и двухфазное состояние вещества. Положение этой прямой может быть определено, если к замкнутому обратимому циклу 1234531 применить второе начало термодинамики в записи Клаузиуса (2.13.7):

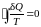. (3.6.1)

Поскольку вдоль всего пути 1234531 температура вещества остается неизменной (ибо этот путь составлен из участков двух возможных вариантов одной и той же изотермы), то последнее уравнение может быть записано в виде

.

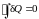Подставляя в это соотношение значение из первого закона термодинамики и учитывая, что

,

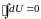получаем для рассматриваемого цикла:

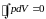. (3.6.2)

Проделаем с последним равенством очевидные преобразования

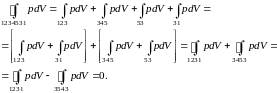(3.6.3)

Откуда находим

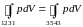, (3.6.4)

т. е. горизонтальную прямую 135 нужно провести так, чтобы заштрихованные на рис. 53 площади были равны.

Как было уже отмечено, в критической точке изотерма 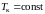имеет касательную и перегиб, поэтому в этой точке должны выполняться соотношения

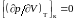, (3.6.5)

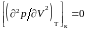, (3.6.6)

где запись 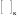означает, что соответствующие производные вычисляются при значениях параметров вещества, равным критическим. Записав уравнение Ван-дер-Ваальса в виде

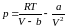, (3.6.7)

вычислив затем производные 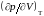и 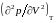, приравняв их к нулю, нетрудно получить

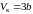, (3.6.8)

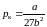, (3.6.9)

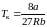. (3.6.10)

Из выражений (3.6.8–3.6.10) следует, что соотношение

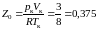(3.6.11)

не зависит от природы вещества. Опыт же показывает, что величина 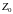имеет разные значения для различных газов: для водорода она равна 0,33, для кислорода – 0,29, для углекислого газа – 0,22. Эти существенные расхождения величины с экспериментальными данными свидетельствуют, что уравнение Ван-дер-Ваальса, из которого эта величина получена, является приближенным, хотя качественная картина изменения состояния вещества передается уравнением достаточно правильно. Известно большое число попыток получения более точного уравнения состояния вещества. Однако эти уравнения содержат большое число поправочных коэффициентов, физический смысл которых неясен, как в уравнении Ван-дер-Ваальса.

В наиболее общем виде методами статистической физики академиком Н. Н. Боголюбовым получено уравнение состояния

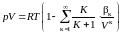, (3.6.12)

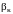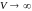где – так называемые вириальные коэффициенты, которые являются функциями только температуры. Из уравнения Боголюбова следует, что чем большее значение молярного объема , тем меньшее число членов ряда следует учитывать для получения достаточно точного результата. При все члены степенного ряда обращаются в нуль, и уравнение (3.6.12) приобретает вид , т. е., как и следовало ожидать, уравнение Боголюбова превращается в уравнение Менделеева – Клапейрона. Вириальные коэффициенты не могут быть вычислены чисто теоретическими методами и поэтому должны определяться с помощью экспериментальных данных. Однако эта задача оказывается настолько сложной, что более целесообразным является получение уравнения состояния просто в виде интерполяционной формулы, описывающей экспериментальные данные.