
- •2. Статистический и термодинамический методы изучения систем многих частиц.
- •3. Массы атомов и молекул. Количество вещества.
- •4. Молекулярные силы
- •5. Агрегатные состояния вещества. Характер теплового движения в этих состояниях. Особенности теплового движения в различных агрегатных состояниях вещества.
- •6. Понятие вероятности. (Частотное и априорное определения вероятности события.)
- •7. Некоторые теоремы теории вероятности. (Теоремы сложения и умножения вероятностей. Условие нормировки вероятностей.)
- •8. Интегральная функция распределения. Случайные величины. Интегральная функция распределения случайной величины и её свойства.
- •9. Плотность вероятности и её свойства.
- •10. Средние значения случайных величин. (математическое ожидание). Среднее по времени и среднее по ансамблю. Эргодическая гипотеза (без доказательства).
- •11. Дисперсия и её свойства.
- •15. Модель идеального газа.
- •16. Равновесные состояния и процессы. Термодинамическое равновесие. Равновесные процессы.
- •17. Распределения молекул газа по направлениям движения в состоянии равновесия.
- •18. Число ударов молекул о стенку сосуда (о единицу площади за единицу времени).
- •19. Основное уравнение молекулярно-кинетической теории газов для давления. (Давление иг с точки зрения мкт.)
- •20. Температура и ее измерение. Эмпирические (Опытные) температурные шкалы. Идеально-газовая шкала температур.
- •21. Температура – мера средней кинетической энергии поступательного движения молекул. Молекулярно-кинетический смысл температуры.
- •22. Уравнение Менделеева – Клапейрона (Уравнение состояния идеального газа). Законы идеального газа (следствия из этого уравнения).
- •25. Распределение Максвелла для относительных скоростей (формула).
- •26. Экспериментальная проверка распределения Максвелла (опыт Штерна, опыт Ламерта).
- •27. Распределение Больцмана. Идеальный газ во внешнем поле сил. Барометрическая формула.
- •28. Распределение Максвелла-Больцмана
- •29. Понятие об отрицательных абсолютных температурах.
- •30. Флуктуация. Зависимость относительной флуктуации от числа частиц в системе. Роль флуктуации в науке и технике.
- •31. Теорема о равномерном распределении энергии теплового движения по степеням свободы. Число степеней свободы молекул. Средняя энергия теплового движения молекул газа.
- •32. Броуновское движение. Проверка распределения Больцмана в опытах с броуновским движением. Формула Эйнштейна для описания броуновского движения.
- •33. Внутренняя энергия. Термодинамический метод. Выражение для внутренней энергии идеального газа.
- •34. Работа и количество тепла. Первый закон термодинамики. Работа при равновесном и неравновесном изменении объема системы.
- •35. Теплоемкость. Применение 1-го начала термодинамики для вычисления теплоемкости вещества.
- •36. Теплоемкость молекулярного водорода (экспериментальная). Классическая теория теплоемкостей идеального газа. Ограниченность теоремы о равномерном распределении энергии по степеням свободы.
- •38. Адиабатный процесс. Уравнение адиабаты идеального газа. Работа идеального газа при адиабатическом изменении его объема.
- •39. Политропные процессы. Уравнение политропы идеального газа. Работа идеального газа при политропическом процессе.
- •40. Обратимые и необратимые процессы.
- •41. Круговые термодинамические процессы и циклы. Тепловые и холодильные машины. Работа при круговом процессе. Первое начало термодинамики в применении к круговому процессу.
- •42. Второе начало термодинамики в формулировках Кельвина и Клаузиуса, их эквивалентность. Недостаточность первое начала термодинамики для однозначного описания процессов, происходящих в природе.
- •43. Цикл Карно и его кпд.
- •44. Теоремы Карно. Кпд цикла Карно – верхний предел кпд тепловых машин.
- •45. Равенство Клаузиуса. Энтропия. Свойства энтропии. Математическое выражение второго начала термодинамики для обратимых процессов. Постоянство энтропии при обратимых процессах в замкнутой системе.
- •46. Основное уравнение термодинамики для обратимых процессов. Энтропия идеального газа.
- •48. Свободная энергия системы.
- •51. Уравнение Клапейрона-Клаузиуса (дифференциальное).
- •52. Уравнение Ван-дер-Ваальса – Уравнение состояния неидеальных газов. Опытное определение констант уравнения Ван-дер-Ваальса.
- •54. Внутренняя энергия газа Ван-дер-Ваальса. Адиабатическое расширения газа ВдВ в пустоту.
- •55. Эффект Джоуля-Томсона. Общая термодинамическая теория дифференциального эффекта Джоуля-Томсона.
- •56. Эффект Джоуля-Томсона в газе Ван-дер-Ваальса.
- •57. Сжижение газов. Получение низких и сверхнизких температур. Метод магнитного охлаждения.
- •58. Среднее число столкновений и средняя длина свободного пробега молекул. Эффективный диаметр газовых молекул. Понятие об эффективном сечении процесса столкновения частиц.
- •59. Общее уравнение явлений переноса. Явления переноса. Общее уравнение явлений переноса в газах.
- •60. Теплопроводность. Уравнение теплопроводности. Основной закон теплопроводности – закон Фурье. Вычисление и экспериментальное определение коэффициента теплопроводности.
- •61. Внутреннее трение (вязкость) газов. Основной закон вязкости – закон Ньютона. Вычисление (и экспериментальное определение) коэффициента вязкости.
- •62. Диффузия. Основной закон диффузии – закон Фика. Вычисление коэффициента самодиффузии газов.
- •63. Некоторые свойства разреженных газов. Физические явления в сильно разреженных газах. Определение вакуума. Течение и равновесие газов в условиях вакуума. Молекулярное течение. Тепловая эффузия.
- •64. Теплопроводность и вязкое трение в ультраразреженных газах.
- •65. Общие свойства жидкостей.
- •66. Молекулярное давление и поверхностное натяжение жидкостей.
- •67. Явления на границе жидкости и твердого тела.
- •68. Избыточное давление под искривленной поверхностью жидкости. Формула Лапласа.
- •69. Капиллярные явления.
- •70. Давление насыщенного пара над искривленной поверхностью жидкости.
- •72. Кипение. Перегрев жидкостей.
- •74. Кристаллические решетки. Решетки Браве. Элементы симметрии решетки. Классификация решеток Браве по кристаллографическим системам.
- •77. Плавление, кристаллизация и возгонка (сублимация) твердых тел.
- •78. Теплоемкость твердых тел. Классическая теория и ее недостатки.
- •79. Фазовая диаграмма кристалл-жидкость-газ. Тройная точка.
- •80. Фазовые переходы первого и второго рода. Фазовая диаграмма гелия.
38. Адиабатный процесс. Уравнение адиабаты идеального газа. Работа идеального газа при адиабатическом изменении его объема.
Адиабатным называют такой процесс, в котором к системе не подводится тепло и от системы не отводится тепло. При адиабатном процессе должна быть обеспечена идеальная теплоизоляция от внешней среды, в отличие от изотермического процесса, требующего идеального теплового контакта со средой. В реальных условиях процесс является адиабатным, если система снабжена хорошей теплоизоляцией или если процесс протекает настолько быстро, что не происходит заметного теплообмена с внешней средой.
Из первого закона
термодинамики следует, что при адиабатном
процессе
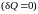 работа производится только за счет
изменения внутренней энергии вещества:
работа производится только за счет
изменения внутренней энергии вещества:
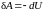 . (2.7.24)
. (2.7.24)
Соотношение (2.7.24) можно записать и в интегральной форме:
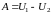 . (2.7.25)
. (2.7.25)
Если вещество
расширяется и совершает работу над
внешними телами, то
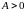 и, как следует из (2.7.25) ,
и, как следует из (2.7.25) ,
 ,
т. е. внутренняя энергия вещества
уменьшается. Это и понятно: в адиабатном
процессе к системе нет притока теплоты
извне и единственный источник энергии
для совершения работы – это внутренняя
энергия самой системы. Соотношения
(2.7.24–2.7.25) справедливы для любых адиабатных
процессов: равновесных или неравновесных,
для любых веществ, находящихся в любых
агрегатных состояниях, так как они
являются следствием закона сохранения
энергии.
,
т. е. внутренняя энергия вещества
уменьшается. Это и понятно: в адиабатном
процессе к системе нет притока теплоты
извне и единственный источник энергии
для совершения работы – это внутренняя
энергия самой системы. Соотношения
(2.7.24–2.7.25) справедливы для любых адиабатных
процессов: равновесных или неравновесных,
для любых веществ, находящихся в любых
агрегатных состояниях, так как они
являются следствием закона сохранения
энергии.
Для идеального газа формула (2.7.24) приобретает вид:
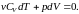 (2.7.26)
(2.7.26)
Отсюда видно, что
при адиабатном расширении
газ охлаждается
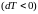 ,
а при адиабатном сжатии
газ нагревается
,
а при адиабатном сжатии
газ нагревается
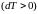 ,
хотя теплота при этом процессе не
подводится и не отводится.
,
хотя теплота при этом процессе не
подводится и не отводится.
Проинтегрировав соотношение (2.7.26), найдем работу, совершаемую идеальным газом при адиабатном процессе.
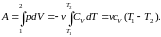 (2.7.27)
(2.7.27)
Теплоемкость вынесена из-под интеграла, т. к. для идеального газа она не зависит от температуры.
Чтобы найти
уравнение адиабаты в переменных
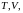 подставим в формулу (2.7.26) вместо p
его выражение из уравнения Менделеева
–Клапейрона
подставим в формулу (2.7.26) вместо p
его выражение из уравнения Менделеева
–Клапейрона
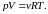 В результате будем иметь
В результате будем иметь
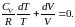 (2.7.28)
(2.7.28)
Интегрирование последнего соотношения дает
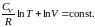 (2.7.29)
(2.7.29)
Откуда находим
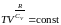 . (2.7.30)
. (2.7.30)
Выразим величину
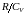 через отношение теплоемкостей
через отношение теплоемкостей
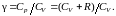 В результате будем иметь
В результате будем иметь
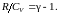 Подставив это значение в (2.7.30), получим
Подставив это значение в (2.7.30), получим
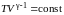 . (2.7.31)
. (2.7.31)
Последнее соотношение есть уравнение адиабаты (уравнение Пуассона) в переменных T,V. Чтобы записать это уравнение в координатах p,V или T,p нужно произвести замену соответствующих переменных в (2.7.31), воспользовавшись уравнением Менделеева – Клапейрона. В результате получим еще два эквивалентных уравнения адиабаты:
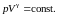 (2.7.32)
(2.7.32)
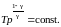 (2.7.33)
(2.7.33)
Выражение для работы (2.7.27) можно записать иначе. Для этого уравнение адиабаты (2.5.31) представим в виде:
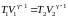 . (2.7.34)
. (2.7.34)
Отсюда находим
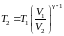 . (2.7.35)
. (2.7.35)
Подставляя (2.7.35)
в (2.7.27) и учитывая что
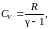
получим
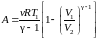 . (2.7.35a)
. (2.7.35a)
Из уравнения
Пуассона (2.7.32) следует, что давление
идеального газа в адиабатном процессе
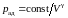 убывает быстрее, чем в изотермическом
процессе
убывает быстрее, чем в изотермическом
процессе
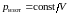 ,
так как всегда
,
так как всегда
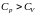 и, таким образом,
и, таким образом,
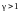 .
Физически это объясняется тем, что при
адиабатном расширении давление газа
уменьшается не только за счет уменьшения
объема, но и по причине происходящего
при этом понижении температуры. Поэтому
и работа против меньшего внешнего
давления
.
Физически это объясняется тем, что при
адиабатном расширении давление газа
уменьшается не только за счет уменьшения
объема, но и по причине происходящего
при этом понижении температуры. Поэтому
и работа против меньшего внешнего
давления
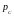 (
(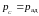 для равновесного процесса) при адиабатном
процессе будет меньше, чем работа против
большего внешнего давления
для равновесного процесса) при адиабатном
процессе будет меньше, чем работа против
большего внешнего давления
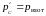 при изотермическом процессе. На рис. 29
работа расширения от объема
до объема
при адиабатном процессе равна площади
фигуры
при изотермическом процессе. На рис. 29
работа расширения от объема
до объема
при адиабатном процессе равна площади
фигуры
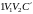 ,
а при изотермическом – площади фигуры
,
а при изотермическом – площади фигуры
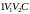 .
.
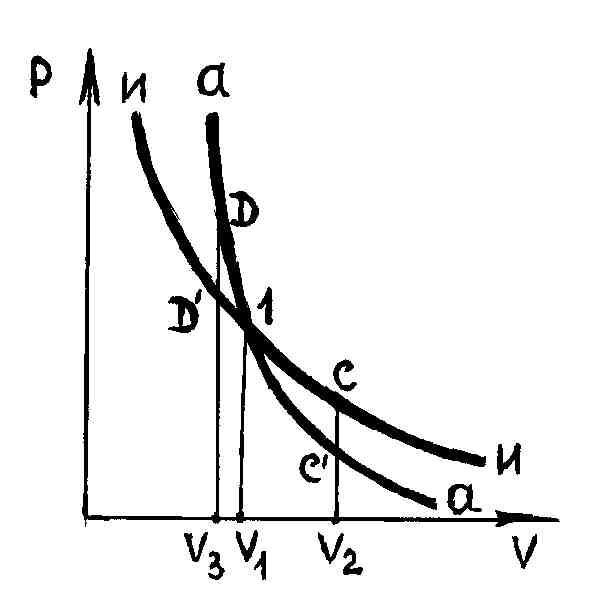
Р и с. 29
Наоборот, при
адиабатном сжатии от объема
до объема
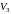 давление газа растет быстрее, чем при
изотермическом процессе, так как при
адиабатном процессе давление увеличивается
не только за счет уменьшения объема, но
и вследствие роста температуры газа.
Поэтому и работа при адиабатическом
сжатии, равная площади фигуры
давление газа растет быстрее, чем при
изотермическом процессе, так как при
адиабатном процессе давление увеличивается
не только за счет уменьшения объема, но
и вследствие роста температуры газа.
Поэтому и работа при адиабатическом
сжатии, равная площади фигуры
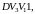 больше работы сжатия при изотермическом
процессе, равной площади фигуры
больше работы сжатия при изотермическом
процессе, равной площади фигуры
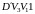 .
.
В заключение
параграфа заметим, что согласно (2.7.25)
изменение внутренней энергии
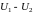 при адиабатном процессе можно вычислять
по формулам (2.7.27) и (2.7.27a).
при адиабатном процессе можно вычислять
по формулам (2.7.27) и (2.7.27a).
