29. Понятие об отрицательных абсолютных температурах.

Отрицательная абсолютная температура, величина, вводимая для описания неравновесных состояний квантовой системы, в которых более высокие уровни энергии более населены, чем нижние. В равновесном состоянии вероятность иметь энергию E_n определяется формулой:

. (1)

Здесь E_i — уровни энергии системы, k — постоянная Больцмана, Т — абсолютная температура, характеризующая среднюю энергию равновесной системы U = Σ (W_nE_n), Из (1) видно, что при Т > 0 нижние уровни энергии более населены частицами, чем верхние. Если система под влиянием внешних воздействий переходит в неравновесное состояние, характеризующееся большей населённостью верхних уровней по сравнению с нижними, то формально можно воспользоваться формулой (1), положив в ней Т < 0. Однако понятие О. т. применимо только к квантовым системам, обладающим конечным числом уровней, так как для создания О. т. для пары уровней необходимо затратить определённую энергию.

         В термодинамике абсолютная температура Т определяется через обратную величину 1/Т, равную производной энтропии S по средней энергии системы при постоянстве остальных параметров х:

. (2)

        Из (2) следует, что О. т. означает убывание энтропии с ростом средней энергии. Однако О. т. вводится для описания неравновесных состояний, к которым применение законов равновесной термодинамики носит условный характер.

         В более узком смысле О. т.— характеристика степени инверсии населённостей двух выбранных уровней энергии квантовой системы. В случае термодинамического равновесия населённости N₁ и N₂ уровней E₁ и E₂ (E₁ < E₂), т. е. средние числа частиц в этих состояниях связаны формулой Больцмана:

, (3)

где Т — абсолютная температура вещества. Из (3) следует, что N₂ < N₁. Если нарушить равновесие системы, например, воздействовать на систему монохроматическим электромагнитным излучением, частота которого близка к частоте перехода между уровнями: ω₂₁ = (E₂ — E₁)/ħ и отличается от частот других переходов, то можно получить состояние, при котором населённость верхнего уровня выше нижнего N₂ > N₁. Если условно применить формулу Больцмана к случаю такого неравновесного состояния, то по отношению к паре энергетических уровней E₁ и E₂ можно ввести О. т. по формуле:

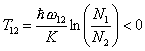. (4)

        Несмотря на формальный характер этого определения, оно оказывается в ряде случаев удобным, например позволяет описывать флуктуации в равновесных и неравновесных системах с О. т. аналогичными формулами. Понятием О. т. пользуются в квантовой электронике для удобства описания процессов усиления и генерации в средах с инверсией населённости.

30. Флуктуация. Зависимость относительной флуктуации от числа частиц в системе. Роль флуктуации в науке и технике.

Флуктуацией называют случайное отклонение физических величин от их средних значений. За количественную меру флуктуации принима­ют среднеквадратическое значение случайной величины

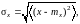
Флуктуации макроскопических величин вызываются беспорядочным тепловым движением молекул, образующих рассматриваемую систему.

Даже в состоянии равновесия наблюдаемые физические величины испытывают флуктуации около своих средних значений. Это легко заметить на опыте при измерении, например, величины давления рав­новесного состояния газа двумя разными манометрами: быстродейству­ющим (чувствительным) и инерционным (грубым) (рис. 19).

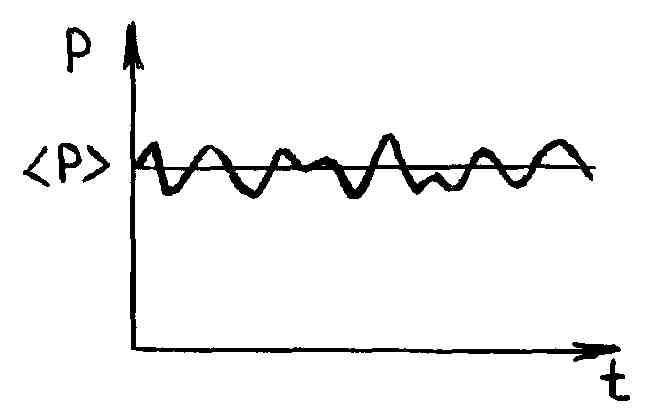
Р и с. 19

Из рис. 19 видно, что инерционный манометр показывает постоянное, равное среднему, давление, тогда как быстродействующий, успевая реа­гировать на малые изменения действующей на него силы, обнаруживает колебания около среднего значения.

Если система состоит из N невзаимодействующих молекул, то относительная флуктуация любой аддитивной физической величины Ф, значение кото­рой для всей системы в целом равно сумме ее значений φ_i для всех молекул, убывает обратно пропорционально корню квадратному из чис­ла молекул в системе. Докажем это утверждение.

Рассмотрим аддитивную величину Ф, например, суммарную кинетическую энергию хаотического теплового движения N молекул. Тогда

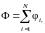
где 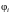– кинетическая энергия i-й молекулы. Среднее значение

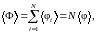(1.16.1)

так как в состоянии равновесия для одинаковых молекул их средние равны, т. е.

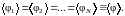
При вычислении дисперсии величины Ф учтем, что дисперсия суммы независимых (невзаимодействующих) величин равна сумме их дисперсий, т. е.

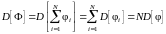. (1.16.2)

Извлекая корень квадратный из обеих частей (1.16.2), получим соотношение для среднеквадратических величин, т. е.

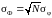. (1.16.3)

Таким образом, абсолютная флуктуация аддитивной величины Ф растет пропорционально 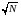. Однако важна не абсолютная флуктуация величины Ф, существенным является во сколько раз она меньше среднего значения Ф, возле которого происходят эти флуктуации, т. е. имеет значение относительная флуктуация:

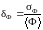. (1.16.4)

Подставляя (1.16.1) и (1.16.3) в (1.16.4), получим

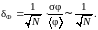(1.16.5)

Из соотношения (1.16.5) следует, что относительные флуктуации всех физических величин, значения которых для всей системы равно сумме значений их для всех молекул, обратно пропорционально корню из числа частиц в системе. Так как число молекул в макроскопической системе обычно порядка числа Авогадро ( ), то , что является ничтожно малой величиной. Это означает, что величина флуктуации меньше среднего значения 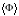примерно в 1012 раз. Если обратиться к рис. 19, то такие флуктуации давления невозможно изобразить ни в каком линейном масштабе: они просто сольются с прямой, соответствующей . 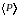Поэтому можно утверждать, что средние значения макроскопических величин Ф при большом числе молекул в рассматриваемой системе совпадают с их истинными (измеримыми на опыте) значениями. Однако, если число молекул в рассматриваемой системе невелико, то истинное значение Ф будет существенно отличаться от среднего значения Ф.