1. Предмет молекулярной физики. Понятие о микроскопическом и макроскопическом состояниях системы. Основные положения молекулярно-кинетической теории строения вещества. Способы изменения энергии системы.

Молекулярная физика – раздел курса общей физики, в котором изучаются макроскопические свойства вещества, обусловленные его молекулярным строением, характером движения молекул и силами, действующими между ними.

Объектом исследования является система, состоящая из множества молекул.

Предметом исследования является свойства вещества и происходящие в них процессы.

Цель – нахождение зависимости между макроскопическими системами частиц.

Микроскопическое состояние системы — это состояние системы, определяемое заданием координат и импульсов всех составляющих систему частиц.

Макроскопическое состояние системы — это состояние системы, характеризуемое небольшим числом величин (Р, V, T).

T, V, p – макроскопические величины.

Молекулярно-кинетической теорией называют учение о строении и свойствах вещества на основе представления о существовании атомов и молекул как наименьших частиц химических веществ.

В основе молекулярно-кинетической теории лежат три основных положения:

1. Все вещества – жидкие, твердые и газообразные – образованы из мельчайших частиц – молекул, которые сами состоят из атомов («элементарных молекул»). Молекулы химического вещества могут быть простыми и сложными, т.е. состоять из одного или нескольких атомов. Молекулы и атомы представляют собой электрически нейтральные частицы. При определенных условиях молекулы и атомы могут приобретать дополнительный электрический заряд и превращаться в положительные или отрицательные ионы.

2. Атомы и молекулы находятся в непрерывном хаотическом движении.

3. Частицы взаимодействуют друг с другом силами, имеющими электрическую природу. Гравитационное взаимодействие между частицами пренебрежимо мало.

Существуют два способа изменения внутренней энергии системы — совершение механической работы над системой и теплообмен с другими системами.

Первый способ изменения внутренней энергии — совершение механической работы А' внешними силами над системой или самой системой над внешними телами А (А = -А'). При совершении работы внутренняя энергия системы изменяется за счет энергии внешнего источника.

Второй способ изменения внутренней энергии системы (без совершения работы) называется теплообменом (теплопередачей). Количество энергии, полученное или отданное телом при таком процессе, называется количеством теплоты и обозначается ΔQ.

2. Статистический и термодинамический методы изучения систем многих частиц.

В статистическом методе микроскопические величины, характеризующие движение молекулы (к примеру, ее импульс в данный момент времени), являются непредсказуемыми, случайными. Для построения теории создается гипотетическая модель механизма молекулярного движения и пространственного строения вещества. Затем в этой модели разрабатываются методы нахождения плотности вероятностей тех или иных величин, зная которые вычисляют средние значения этих величин.

В термодинамическом методе исследования вещества, в отличие от статистического, не вводятся в рассмотрение какие-либо модельные представления об атомно-молекулярном строении тела, а ставится своей задачей установление зависимости между непосредственно наблюдаемыми макроскопическими (измеряемыми в опыте) величинами, такими как давление, температура, объем, концентрация, напряженность электрического или магнитного поля и т. п. Термодинамика как теоретическая дисциплина строится на трех фундаментальных законах (началах), установленных на основании огромного опытного знания, относящегося к поведению макроскопических систем. Выводы термодинамики имеют весьма общий характер, независимый от выбора гипотетической модели структуры вещества, независимо от характера движения молекул, взаимодействия между ними. Результаты, получаемые в статистической теории, существенным образом зависят от выбора этой гипотетической модели. Недостатком термодинамического метода является невозможность с помощью его вскрыть молекулярную сущность изучаемых явлений. Термодинамика ничего не говорит о механизме происходящих в веществе микропроцессов, а только устанавливает связь между макроскопическими характеристиками вещества. Поэтому в настоящее время в молекулярной физике при исследовании макроскопических свойств вещества разрабатываются оба подхода: статистический и термодинамический. Эти исследования взаимно дополняют друг друга, так как у них один и тот же объект исследования – система, состоящая из многих молекул, и одна и та же цель – нахождение зависимостей между макроскопическими величинами системы частиц.

3. Массы атомов и молекул. Количество вещества.

Так как массы атомов и молекул чрезвычайно малы (10^–25–10^–27кг), то их удобно измерять не в килограммах, а в специальных относительных единицах. В качестве единичной атомной массы m_ед принимается двенадцатая часть массы изотопа углерода ¹²С. Эта величина имеет следующее значение:

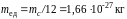. (1)

Относительной атомной единицей массы 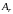называется отношение массы данного атома m_ат к атомной единице массы m_ед, т. е.

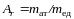. (2)

Величины определяют экспериментально и их значения для химических элементов приведены в таблице Менделеева.

Относительная молекулярная масса 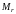молекулы вычисляется по аналогичной формуле:

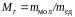. (3)

Относительные молекулярные массы с достаточной точностью могут быть найдены в виде суммы относительных атомных масс, составляющих молекулу. Известно, что масса молекулы меньше составляющих ее масс атомов на величину дефекта массы Δm, который определяется по формуле Эйнштейна Δm = ΔЕ /c², где ΔЕ – суммарная энергия связи атомов в молекуле, а с – скорость света. Для молекул, содержащих небольшое число атомов ΔЕ ~ 10 эВ = 1,6 ·10^–18 Дж этой энергии соответствует дефект массы Δm ~ 10^–35 кг, что в сто миллионов раз меньше масс молекул. Поэтому величиной дефекта массы пренебрегают. Зная для данной молекулы, легко найти ее массу

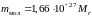. (4)

В системе единиц СИ количество вещества выражается в молях. Молем называют количество вещества, содержащее столько частиц (молекул, атомов, электронов, фотонов и т. д.), сколько атомов содержится в 12 г изотопа углерода ¹²C. Это число называют постоянной Авогадро N_A. Согласно определению

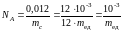. (5)

Учитывая (1), получим

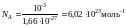. (6)

Массу одного моля называют молярной массой. Очевидно, что молярная масса

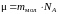. (7)

С учетом (3) и (5), выражение (7) примет вид

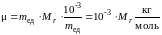. (8)

Число  молей связано с числом N молекул, содержащихся в данном количестве вещества, соотношением

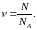(9)

Умножив числитель и знаменатель выражения (9) на массу m_мол молекулы, получим

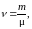(10)

где m – масса N молекул вещества.