Юрий Кругляк_Квантовое моделирование в квантовой химии на квантовых компьютерах_399_стр

В [62] показано, что модель АКВ в вычислительном плане эквивалентна модели квантовых схем, имея в виду, что алгоритмы, записанные в одной модели могут быть переписаны в алгоритмы, записанные в другой модели, без какой-либо существенной потери в эффективности вычислений. В противовес этому, БМВ не обладает таким свойством [63]. Однако, эта модель позволяет решать задачи, не подъемные для классического компьютера [64]. БМВ подробно обсуждается в §§ 7.3.3, 7.5.3.2.

Кроме непосредственных вычислений на квантовых компьютерах важную роль на пересечении между компьютерными науками и квантовой физикой, имеющем прямое отношение к квантовой химии, играет теория сложности квантовых вычислений. В качестве примеров назовем нахождение универсального функционала в ТФП [65], проблему N-представимости [66], расчет плотности состояний квантовых систем [67]. Вычислительная сложность в задачах квантовой химии подробно обсуждается в [68].

Взаимоотношение разделов этой главы и последовательность излагаемого далее материала графически проиллюстрирована на рис. 20. Охвачен на рисунке далеко не весь материал. Более подробное и точное наименование всех разделов этой главы дается в оглавлении книги.

Вразделе 7.2 обсуждаются вызовы, стоящие перед классической квантовой химией (гл. 1), рассматриваются приближенные методы расчета статических и динамических свойств молекулярных систем и вводятся в

обсуждение квантовые алгоритмы, позволяющие разрешить проблемы, стоящие перед классической квантовой химией.

Вразделе 7.3 обсуждаются классы сложности классических и квантовых алгоритмов в квантовой химии и в молекулярной вибронике.

Вразделе 7.4 достаточно подробно излагаются квантовые алгоритмы вычисления энергии молекулярных систем, подготовки исходных состояний и вычисления свойств молекулярных систем на помехоустойчивых квантовых компьютерах/ПУКК (Fault-Tolerant Quantum Computers/FTQC) .

Раздел 7.5 посвящен вариационным квантовым алгоритмам, используемым

всовременных промежуточных шумящих квантовых устройствах/ПШКУ

(Noisy Intermediate-scale Quantum/NISQ), включая подготовку исходных состояний, вычисление энергии, методы оптимизации, физическую реализацию ВКА, алгоритмы для возбужденных состояний и вычисление свойств молекул. Этот раздел заканчивается обсуждением других гибридных квантовоклассических алгоритмов в химии и не-вентильных методов в квантовой химии.

210

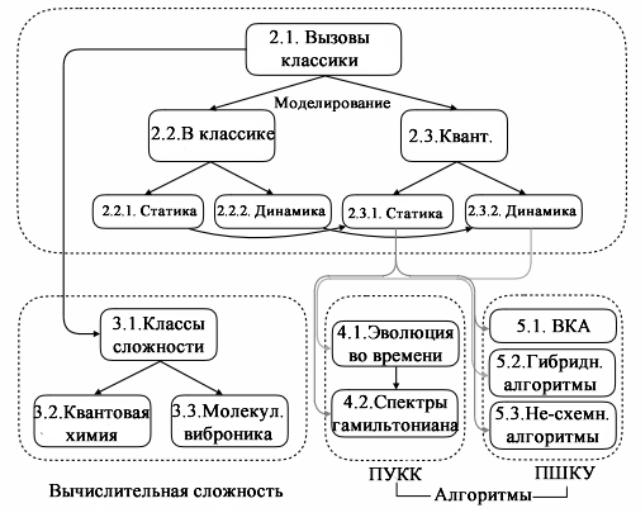
Рис. 20. Взаимоотношения между основными разделами главы 7 в соответствии с оглавлением книги. Статические и динамические свойства обсуждаются в классической квантовой химии (§ 7.2.2) и в рамках квантовых вычислений (§ 7.2.3). Далее следует обсуждение классов вычислительной сложности (§ 7.3.1) в квантовой химии (§ 7.3.2) и в молекулярной вибронике (§ 7.3.3). Рассматриваются алгоритмы для ПУКК (§§ 7.4.1–2) и ПШКУ (§§ 7.5.1–3) [1].

В заключение обсуждаются перспективы применения квантовых компьютеров в квантовой химии, достаточно подробно излагается техника счета и результаты расчета молекулы водорода и в Приложении предлагается вашему вниманию аннотированная библиография новейших исследований и квантово-химических расчетов на квантовых компьютерах, дающая представление о результатах, достигнутых к 2020 году.

211

7.2. Квантовая химия в эру квантовых вычислений

Задача, стоящая перед квантовой химией, заключается в решении уравнения Шредингера для молекулярных систем (§ 1.2). Точное решение уравнения Шредингера известно лишь для атома водорода (при условии фиксированного положения протона в пространстве) и таковое становится недостижимым для более сложных атомных и молекулярных систем в результате экспоненциального роста размера волновой функции по мере увеличения числа частиц в системе [69]. Эта проблема инспирировала разработку множества самых разнообразных приближенных методов решения уравнения Шредингера (гл. 1), достигших совершенства и фактически своего предела с использованием современных битовых компьютеров.

В следующем разделе обсуждаются вызовы, стоящие перед винтажной квантовой химией и выходы за пределы классических ограничений с помощью квантовых компьютеров. Удобства ради, рассматриваются статические и динамические свойства порознь. Под статическими свойствами в первую очередь подразумеваются энергии состояний, прежде всего расчет энергии основного состояния многоэлектронной системы.

7.2.1. Начала и вызовы классической квантовой химии

Любой квантово-химический расчет начинается с задания набора базисных функций, обычно гауссовых (§ 1.3.4). Это не решает проблему экспоненциального роста размера волновой функции, однако, позволяет контролировать точность построения волновой функции.

Врасчетах обычно используется приближение Борна – Оппенгеймера (ПБО/§ 1.2), хотя в пос леднее время прилагаются значительные усилия выйти за пределы ПБО [70 – 73]. Мы сосредоточимся на квантовых вычислениях в режиме ПБО, хотя уже известны успешные попытки выйти за пределы ПБО на квантовых компьютерах [74 – 76].

Впоследние годы популярной техникой избежать проблему размерности многоэлектронной волновой функции стала ТФП [77, 78] (§ 1.3.7.6). Все степени свободы в электронной системе проинтегрированы за исключением плотности. Однако, качество ТФП зависит от выбора обменнокорреляционного функционала. Предпринимаются попытки улучшать функционалы ДФТ на систематической основе, напр., ПОГ, мета-ПОГ, гибридные варианты, однако, нет однозначной рекомендации какие именно функционалы приемлемы для данной электронной системы. Вместе с тем, эти продвинутые подходы нивелируют преимущества стандартной классической

212

ТФП. Большинство функционалов дают приемлемые результаты вблизи равновесной геометрии молекулярной системы, однако, ведут себя непредсказуемо в случае сильной электронной корреляции или в ситуации с сильным дисперсионным взаимодействием, например, при разрыве химической связи или в процессах сольватации. Несмотря на перечисленные недостатки расчеты в моделях ТФП проводятся и на квантовых компьютерах.

Еще один способ избежать экспоненциального роста размера волновой функции заключается в использовании модели ССП (§ 1.3.6). Хотя корреляционные эффекты при этом не учитываются, самосогласованные волновые функции могут служить хорошим приближением для построения более точных функций.

Точное решение уравнения Шредингера при заданном фиксированном орбитальном базисе заключается в учете всех возможных возбужденных электронных конфигураций и известно как полное конфигурационное взаимодействие, ПКВ (§ 1.3.7.1.2). Волновой функцией ПКВ невозможно манипулировать на классическом битовом компьютере из-за ее размерности. Разработаны различные подходы, промежуточные между однодетерминантной волновой функцией ССП и волновой функцией ПКВ. Эти подходы и соответствующие модели нашли применение в квантово-химических расчетах на квантовых компьютерах, к рассмотрению которых мы переходим.

7.2.2. Классические приближенные методы и их ограничения

Квантовые вычисления предложили методы, способные ответить на вызовы классической квантовой химии. Соответствующие квантовые алгоритмы рассматриваются далее в § 7.2.3. Тем не менее, необходимо отметить, что в классической квантовой химии были предложены различные подходы и методы, которые пытались ответить на вызовы винтажной квантовой химии на классических битовых компьютерах. Мы далее рассматриваем эти методы как мотивирующие разработку квантовых алгоритмов.

7.2.2.1.Статические свойства: волновые функции и энергетические спектры

7.2.2.1.1. Теория связанных кластеров

Метод связанных кластеров (§ 1.3.7.5) [79] формулируется как компактная параметризация волновой функции посредством экспоненциального функционала кластерного оператора. Соответствующие алгоритмы реализуют

213

приближения, приемлемые для классических компьютеров. Предложенные машинные коды обычно используют преобразование подобия кластерного оператора как оператора обычного возбуждения, используя преимущества сходимости рядов Бейкера – Кэмпбелла – Хауссдорфа. Это приводит к неэрмитовости задачи и требует проектирования на небольшое подпространство и введения дополнительных приближений для вычисления кластерных амплитуд. Хотя такая формулировка теории связанных кластеров все еще является точной в пределе N-частичного оператора возбуждения, в практических расчетах операторы возбуждения усечены, что не может гарантировать достоверность результатов вычисления. Несостоятельность теории связанных кластеров с учетом только однократно- и двукратновозбужденных конфигураций в явлениях диссоциации молекул хорошо известна [80]. Подобное поведение можно прогнозировать при любом усечении оператора возбуждения, если для гамильтониана характерна сильная корреляция [81]. Известно несколько подходов [82, 83] по улучшению этой ситуации путем аппроксимации кластерных операторов высокого порядка или путем учета статических корреляционных эффектов. Исследования в этом направлении все еще активно ведутся.

Хотя теория связанных кластеров и остается многообещающим методом расчета в квантовой химии, его неэрмитовая формулировка приводит к невозможности вычисления энергии вариационным методом. Вариационно приемлемая модель связанных кластеров [84] решает эту проблему, однако, соответствующий расчетный метод на классических компьютерах применим лишь к небольшим электронным системам [85 – 87] или к моделям с усеченным пространством состояний [88]. Введение комплексно сопряженных операторов возбуждений подразумевает свертки между бра- и кет-операторами. Трансформированный таким образом гамильтониан есть полный N-частичный оператор с числом слагаемых порядка N! Проблема становится еще более непробиваемой, если операторы в экспонентах не являются чистыми операторами возбуждений. В этом случае подлежащие вычислению средние значения демонстрируют свертки между кластерными операторами и число их бесконечно велико. Унитарная теория связанных кластеров [89], в которой операторы возбуждения и девозбуждения скомбинированы в унитарный кластерный оператор, и обобщенный метод связанных кластеров [90], в котором кластерный оператор лишен специфической структуры, относятся к тому же классу проблем. Обратим внимание на то, что в квантовом компьютере физические операторы на кубитах часто реализуются посредством унитарных

214

операторов. Если кластерный оператор можно представить низкоуровневой квантовой схемой, то подготовка волновой функции унитарной теории связанных кластеров может быть эффективной. Этот подход к подготовке состояний вместе с классической оптимизацией (§ 7.5.1) делает унитарную теорию связанных кластеров пригодной для гамильтонианов общего вида.

7.2.2.1.2. Квантовый метод Монте-Карло

Квантовый метод Монте-Карло/КМК (Quantum Monte Carlo/QMC) хорошо зарекомендовал себя в крупномасштабных расчетах довольно больших систем в квантовой химии. Заключается он в стохастической оценке энергии для пробной волновой функции

В вариационной формулировке метода Монте-Карло в действительном пространстве радиус-векторы случайным образом расположенных частиц генерируются обычно алгоритмом Метрополиса. Стохастический процесс перебора траекторий заканчивается после достижения достаточной сходимости по энергии.

Разработаны весьма изощренные методы КМК, использующие более совершенные распределения, в частности, диффузионный метод МонтеКарло/ДМК (Diffusion Monte Carlo/DMC), ДМК с фиксацией узлов пробной волновой функции/ДМКФУ (Fixed-Node DMC) и другие.

Предложено несколько алгоритмов, реализующих КМК на квантовых компьютерах [91].

7.2.2.1.3. Метод точной диагонализации

Методы точной диагонализации/ТД (Exact Diagonalization/ED) [79, 92, 93]

обеспечивают точные значения энергии и волновой функции для заданного базисного набора. Примером может служить метод ПКВ. Если метод КМК достигает этого путем экстраполяции, то при реализации ТД выполняется один расчет путем точной диагонализации матрицы гамильтониана без стохастических погрешностей. Достигается это за счет хранения всех коэффициентов разложения по всем возможным детерминантам, что фактически невозможно даже для сравнительно небольших молекул [94, 95] на классических компьютерах. Значительный рост в последние годы вычислительной мощности классических компьютерных кластеров и

215

технологии библиотек не намного улучшают ситуацию [96 – 98]. С переносом расчетов в режиме ПКВ на квантовые компьютеры основные надежды связывают с квантовым алгоритмом вычисления фазы КАВФ (§ 6.6) [38, 99].

7.2.2.1.4. Методы тензорных сетей

По сравнению с обсуждаемыми выше классическими подходами методы тензорного произведения перепутанных состояний [100], которые разработаны для расчета в квантовой химии и в многочастичной физике сильно коррелированных систем, очень близки по духу к моделям квантовых схем, используемых для вычислений на квантовых компьютерах. В случае систем с сильной электронной корреляцией, когда концепция с одной доминирующей конфигурацией не работает, традиционные методы обычно не применимы. В противовес этому эффективными и достаточно точными оказываются методы тензорного произведения [100]. Среди них наиболее часто используется берущий свое начало из квантовой химии метод матрицы плотности ренормализационной группы/МПРГ (Density Matrix Renormalization Group/DMRG) [100 – 109]. Более конкретно, метод МПРГ вариационно оптимизирует волновую функцию в виде матричного произведения состояний/МПС (Matrix Product of States/MPS) [110]:

| ΨMPS = ∑Aα1 Aα2 Aαn |α1α2 αn ,

{α}

которая представляет собой одномерную цепочку тензоров. В квантовохимической интерпретации αi отвечает i-МО, напр., αi {| 0 ,|↓,|↑,|↓↑}.

Вычислительная сложность метода МПРГ определяется размерностью матриц МПС Aαi , которая характеризует перепутывание между различными МО. Концепция МПС допускает компактное представление одномерных систем и удовлетворяет закону площадей [111] в одном измерении. Это позволяет применять метод МПРГ для описания основного состояния одномерных систем со щелью в гамильтониане. Однако, дальнодействующие кулоновские взаимодействия в молекулах вызывают перепутывание МО. Подобные проблемы можно до некоторой степени смягчить путем оптимизации порядка следования орбиталей вдоль одномерной решетки [112, 113] или путем оптимизации базиса [114]. И все же эти проблемы демонстрируют практический предел применимости техники состояний тензорных сетей/СТС

(Tensor Network States/TNS ) в квантовой химии.

Метод МПРГ применительно к задачам квантовой химии может работать со значительным орбитальным пространством (~ 50 MO [115]). Он способен

216

учесть намного большее активное пространство по сравнению с методом ССП [116]. В отдельных случаях метод МПРГ может достичь результатов ПКВ [115, 117]. В случае линейных (квази-линейных) молекулярных систем вполне достижимо активное пространство в сотню МО [118]. Однако, волновые функции МПРГ все же недостаточно учитывают динамическую корреляцию электронов, роль которой в квантовой химии столь велика. Для преодоления этого недостатка разработано несколько методов пост-МПРГ [119 – 127].

Метод СТС [128] является фактически обобщением МПС, направленным на улучшение многоразмерного перепутывания. СТС включает, например, метод проектирования перепутанных парных состояний [129], ветвление СТС/ВСТС (Tree Tensor Network States/TTNS) [130 – 134],

ренормализационный подход к многомасштабному перепутыванию [135] и полнографовый СТС[136, 137].

Коэффициенты разложения волновой функции ПКВ можно представить в виде МПС [110, 138]. В случае расчетного режима ВСТС, который является наиболее общим методом СТС без петель, используется декомпозиция вырожденных значений высокого порядка. Факторизация волновой функции ПКВ в виде МПС не дает никаких вычислительных преимуществ, так что перепутывание двух подсистем в сдвоенной электронной системе приводит к потере квантовой информации [139] и точности.

7.2.2.2. Динамические свойства: временная эволюция волновых функций

Квантовая химия основного состояния молекулярных систем при нулевой температуре охватывает весьма ограниченную область химической науки. Химические процессы идут при конечных температурах, молекулярные системы развиваются во времени и описываются временным уравнением Шредингера

i∂∂t Ψ(r,t) = HΨ(r,t) .

Вслучае независящего от времени гамильтониана решение этого уравнения формально берется в виде

Ψ(r,t) = exp(−iHt)Ψ(r,0) ,

а при переходе к собственным векторам ψ j (r ) независящего от времени гамильтониана

Ψ(r,t) = ∑cj exp(−iE j t)ψ j (r)

j

217

сразу становится очевидной проблема: точное описание эволюции системы во времени требует знания полного энергетического спектра гамильтониана и коэффициентов разложения первоначального состояния по собственным векторам, что в принципе достижимо лишь для очень небольших систем.

Предложено несколько путей приблизиться к решению этой кардинальной проблемы. Далее рассматриваются две довольно широких категории подходов. Методы молекулярной динамики/МД (Molecular Dynamics/MD) избегают рассмотрения эволюции волновой функции в явном виде, ядра рассматривают как классические заряженные частицы и учитывается лишь электростатическое поле, создаваемое электронной плотностью, при фиксированном положении ядер. Другие подходы также избегают рассмотрения динамики полной волновой функции и прибегают к стратегиям, подобным тем, которые рассмотрены в § 7.2.2.1, добавляя лишь формально временную зависимость.

7.2.2.2.1. Молекулярная динамика

При изучении динамики больших химических систем, скажем, в несколько сотен атомов, часто интересуются свойствами, не связанными с квантовыми эффектами. В этом случае достаточно прибегнуть к классическим методам МД, моделируя задачу с использованием эффективных силовых полей и ньютоновской механики [140]. Если же основная задача заключается в нахождении состояний с наинизшей энергией, как, например, при определении наиболее устойчивых конформаций в молекулярных кристаллах или в задачах парковки белок – лиганд, тогда простая динамика неприемлема и прибегают к различным методам оптимизации с целью найти основное состояние системы. Для увеличения точности прибегают к использованию квантово-химических методов ab initio в сочетании с классическими методами МД [141, 142].

Есть немало химических задач, когда нужно учитывать квантовые эффекты, связанные с атомными ядрами, например, эффекты ядерного туннелирования или оценка энергии нулевых колебаний, не учитываемых классической динамикой. Подобные квантовые эффекты необходимо учитывать при моделировании конденсированных гелия и водорода [143] при низких температурах, как впрочем и при высокоточном моделировании таких водородсодержащих систем как жидкая вода при комнатной температуре [144]. Разнообразные методы интегралов по траекториям [145] были предложены для моделирования ядерных квантовых эффектов, в их числе МД в концепции интегралов по траекториям [146], центроидные МД [147] и МД для кольцевых

218

полимеров [148]. Хотя эти методы позволяют частично учитывать квантовые эффекты, они не используют понятие гильбертова пространства, что ограничивает их вычислительные возможности по сравнению с классическим методом МД. Одна из серьезных проблем в МД связана с ограниченным временем прогона, например, при реализации конформационных переходов в гемоглобине [149].

7.2.2.2.2. Квантовая временная эволюция

Большинство методов, упомянутых в § 7.2.2.1, могут быть адаптированы к реализации временной эволюции с сохранением квантового характера на всех ее шагах. Однако, при таком подходе быстро исчерпывается доступная память компьютера и требуется переходить к экспоненциальной матрице гамильтониана [150].

Мёлер и Лоан [151] рассмотрели различные методы аппроксимации экспоненциальных матриц. Разложение Тейлора, аппроксиманты Паде и Чебышева – это методы разложений по степеням гамильтониана [150, 151] для описания оператора эволюции. Они вполне пригодны для небольших матриц, но совершенно неприемлемы для больших систем. Методы обыкновенных дифференциальных уравнений такие, как Рунге – Кутта, являются стандартными для описания временной эволюции классических уравнений. Их можно приспособить и для квантовой эволюции [150, 152], хотя в вычислительном плане они недостаточно эффективны, если речь идет о достижении нужной точности. Полиномиальные методы относятся к другой алгоритмической категории [153, 154]. В этих методах выбирается такой алгоритм работы с экспоненциальной матрицей, чтобы обеспечить требуемую точность, учесть размеры изучаемой системы и простоту имплементации вычислений.

Методы матричной декомпозиции позволяют напрямую аппроксимировать экспоненциальный оператор гамильтона. Примером может служить декомпозиция экспоненты eA = S eV S−1 , где A = SVS−1 , а V диагональная. Этот подход требует намного меньше матричных операций. Наблюдается также бόльшая эффективность и лучшая устойчивость при использовании в декомпозиции треугольных матриц, напр., по Шуру, или блок-диагональных матриц [155]. Известны также методы расщеплений, пригодные для гамильтонианов, выражаемых суммой матриц, если каждый член такой суммы может быть моделирован каким-либо известным эффективным методом. Аналогичная процедура используется в метода Троттера – Судзуки и

219