78. Что показывает частотный спектр сигнала?

В большинстве случаев работу любой системы можно проанализировать, используя в качестве базового сигнала простой синусоидальный сигнал, который описывает гармоническое колебание.

Совокупность простых гармонических колебаний, на которые может быть разложен сложный сигнал, называется частотным спектром сигнала. Для описания частотного спектра сигнала используется ряд Фурье.

(Частотная область гораздо удобнее для определения гармонического состава сигнала. Это нужно, например, для проверки на наличие гармоник несущего сигнала, которые могут вносить помехи в работу других систем, оперирующих на той же частоте, что и гармоники.)

79. В каких единицах измеряются значения амплитудного спектра сигнала?

(!) Под «А» скрывается единица измерения сигнала, потому как для разных сигналов она разная, напр. для ЭЭГ это вольты (мВ, мкВ), а для АД – мм.рт.ст.

Амплитудный спектр сигналаизмеряется в А.

Спектральная мощностьизмеряется в .

Спектральная плотность мощности сигналаизмеряется в 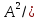Гц.

80. В каких единицах измеряется спектральная мощность и спектральная плотность мощности сигнала?

См 79.

81. Почему более корректно говорить «оценка спектра», а не «спектр»?

Среди методов спектрального оценивания нет таких, которые могли бы с точностью отразить спектр исследуемого сигнала.Вследствие различных допущений и поисков компромисса для лучшего анализа картина истинного спектра искажается.

Например, вычисляемое ДПФ содержитсистематическую (методическую) погрешность анализа. Она является следствием ограничения сигнала по длительности, искажающего результатыспектрального анализа. Применение специальных весовых функций или оконпозволяет сгладить или ослабить вызываемое временным усечением влияниеили эффект разрывов сигнала на краях.

82. Какие известны два наиболее распространённых подхода к получению оценок спектра сигнала?

1.Спектральное оценивание на основе дискретного преобразования Фурье.

В случае использования алгоритма БПФ для получения спектральных оценок возможны два основных варианта: расчет БПФ для всего фрагмента сигнала целиком (периодограммный метод) или использование усреднения спектров, рассчитанных по перекрывающимся фрагментам сигнала (метод Уэлча).

2. Параметрические методы спектрального оценивания

Альтернативный подход к расчету спектральных оценок реализуется с использованием так называемых параметрических методов. Наиболее распространенные из них основаны на модели авторегрессии. (Идея заключается в достижении компромисса между между частотным разрешением СПМ и дисперсией получаемых спектральных оценок.

83. В чём главные достоинства и недостатки классических и параметрических методов спектрального анализа?

	Методы спектрального анализа
	Классические (на основе ДПФ)	Параметрические (авторегрессионные)
Достоинства	Математическая простота. Обратимость ДПФ.	Более реалистические, чем в случае классических методов, предположения о сигнале за пределами анализируемого фрагмента. Возможность анализа спектра по относительно коротким фрагментам сигнала.
Недостатки	Появление спектральной утечки вследствие предполагаемой периодичности сигнала (т.е. нереалистического предположения о сигнале за пределами анализируемого фрагмента). Необходимость наличия относительно продолжительного фрагмента сигнала	Математическая сложность. Необратимость спектра. Необходимость субъективного выбора порядка АР модели. (необходимость контроля результатов человеком-исследователем)

84. В чём различия между непрерывным преобразованием Фурье, рядами Фурье и дискретным преобразованием Фурье?

Ряд Фурье - функциональный ряд, то есть сумма бесконечного числа функций, с базисом (cosnx, sinmx), а преобразование - это функционал, ставящий в соответствие одной функции другую. Дискретное преобразование Фурье основано на дискретизации непрерывных сигналов. Непрерывное преобразование Фурье (спектральное представление сигналов) основано на разложении функций в ряд.

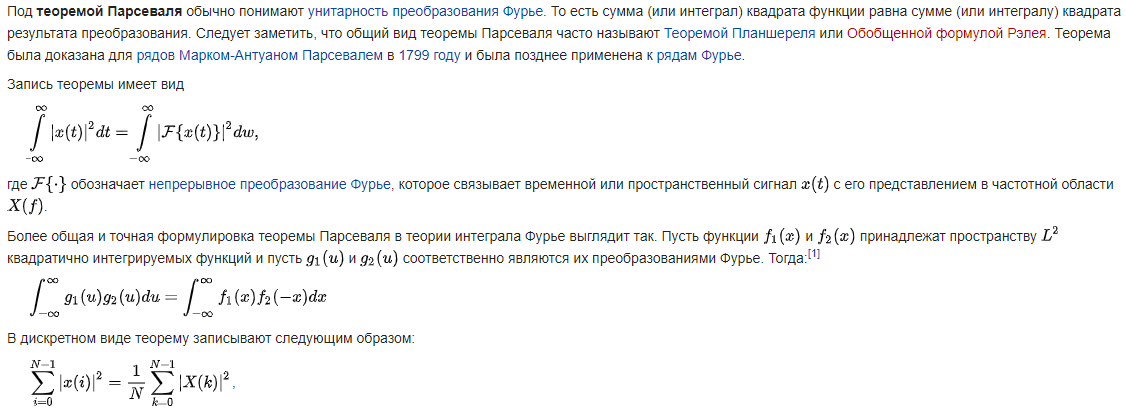
85. Какая связь между преобразованиями Фурье и законом сохранения энергии?

Теорема Парсеваля=ЗСЭ

86. Как отражается на спектральной оценке по методу Фурье взятие конечного отрезка сигнала?

Если исходный сигнал изначально был конечным (скажем, это отдельный импульс) и в преобразование Фурье он попал полностью, то этот подход напрямую дает желаемый результат. Если же во взятый отрезок поместилось не полное количество периодов составляющих гармоник, то будет наблюдаться спектральная утечка.

87. Как отражается на спектральной оценке по методу Фурье дискретизация сигнала?

Значения СПМ известны только для дискретного значения частот с шагом . (График не непрерывный, а дискретный)

88. Как отражается на спектральной оценке по методу Фурье бесконечное периодическое продолжение сигнала?

Часто «конечный» сигнал используемый для преобразования Фурье на самом деле является частью более длинного, возможно бесконечного сигнала, такого как, например, синусоида. В этом случае дополнение конечного отрезка нулями интерпретируют следующим образом: считают что исходный сигнал имеет бесконечно большую длину, но затем умножается на некоторую взвешивающую функцию — “окно”, обращающуюся в ноль вне доступного нам для измерения отрезка. В простейшем случае роль “окна” играет просто прямоугольная функция, соответствующая тому что мы просто дополняем конечный сигнал слева и справа бесконечным числом нулей. В более сложных — исходную последовательность умножают на весовые коэффициенты определяемые функцией “окна” и затем, опять же, дополняют нулями.

Более того спектр будет симметрично повторятся для частот кратных Fs.