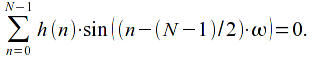38. В чём заключается частотный подход к анализу сигналов?

Наиболее распространенным подходом к обработке и анализу сигналов является частотный подход, при котором предполагается, что рассматриваемый процесс может быть представлен в виде суммы синусоид с различными частотами. Теоретической базой для частотного подхода является теория преобразований и рядов Фурье.

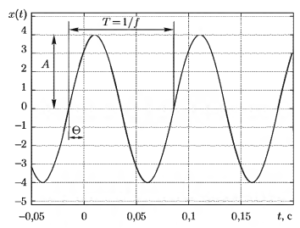
Синусоида полностью определяется формулой 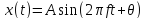, где А — амплитуда; f — частота; θ — фазовый сдвиг (рис. 1).

С точки зрения частотного подхода, процедуры цифровой фильтрации решают задачу целенаправленного изменения амплитуды и фазы каждой из частотных составляющих в соответствии с заданной передаточной функцией. В свою очередь, задачей спектрального анализа является количественная оценка параметров синусоид для всего диапазона исследуемых частот.

39. Почему в преобразованиях выражений для передаточных функций обычно опускают период дискретизации «т» и как учитывается это упрощение в конечном результате?

С целью упрощения математических преобразований их обычно выполняют для нормализованной частоты 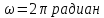, или 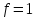Гц, что соответствует 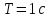. По окончании преобразований переходят обратно к реальным частотам, учитывая частоту дискретизации 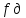. В этом случае выражения для АЧХ и ФЧХ для циклической частоты fпринимают вид

До:

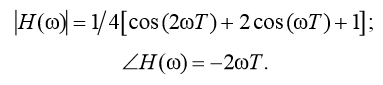
После:

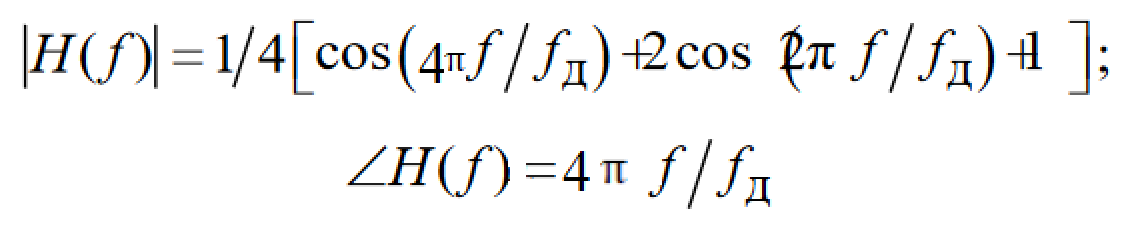
(Пусть наша исходная функция, представляет собой сигнал, записанный в течение Т=1 сек. Тогда период первой гармоники будет равен длительности нашего сигнала Т1=Т=1 сек и частота гармоники равна 1 Гц. Период второй гармоники будет равен длительности сигнала, деленной на 2 (Т2=Т/2=0,5 сек) и частота равна 2 Гц. Для третьей гармоники Т3=Т/3 сек и частота равна 3 Гц. И так далее. Шаг между гармониками в этом случае равен 1 Гц. Таким образом сигнал длительностью 1 сек можно разложить на гармонические составляющие (получить спектр) с разрешением по частоте 1 Гц.)

40. Как называются и как связаны между собой круговая частота «ω» и циклическая частота «f» и в каких единицах они измеряются?

Частота колебаний – это число колебаний, совершаемых телом в единицу времени:

Единица измерения частоты в системе СИ – 1 Герц (Гц).

Циклическая частота – это число колебаний, совершаемых телом за 2pi секунд:

Единица измерения циклической частоты в системе СИ — рад/с.

Частота и циклическая частота связаны между собой формулой:

41. Как связаны между собой частота дискретизации «f» и период дискретизации «Т»?

При цифровой обработке сигналов осуществляют выборку значений аналогового сигнала через равные интервалы времени T. Данный процесс называется дискретизацией сигнала по времени. Время T называют периодом дискретизации, а величину обратно пропорциональную F=1/T – частотой дискретизации.

42. Дать определение z-преобразования.

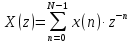
43. Как получить z-преобразование для единичного импульса и единичной ступенчатой последовательности?

Единичный импульс: коэффициенты (1, 0, 0, 0), тогда

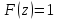
Единичная ступенчатая последовательность: коэффициенты (1, 1, 1, 0, 0), тогда

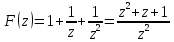
44. Как получить выражение для передаточной функции ЦФ с помощью z-преобразования.

Передаточная функция для z-преобразования:

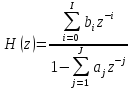
Чтобы перейти к H(jω), используем замену z=e^jωT.

45. Что такое плоскость комплексной переменной «z» и единичная окружность?

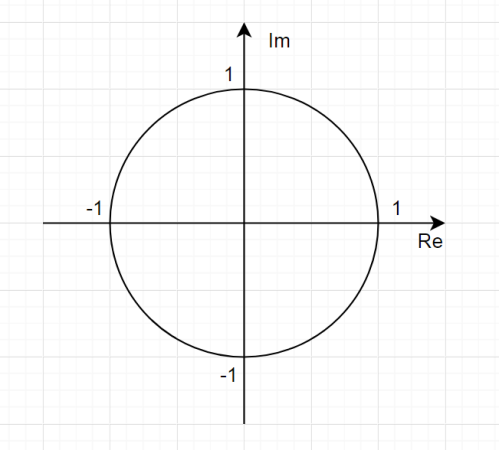
46. Что такое нули и полюса передаточной функции?

Нули – корни числителя передаточной функции.

Полюса – корни знаменателя передаточной функции.

47. Как по положению нулей и полюсов на z-плоскости оценить устойчивость ЦФ?

БИХ фильтр считается устойчивым, если все его полюса лежат внутри единичной окружности.

48. Могут ли нерекурсивные ЦФ быть неустойчивыми и если да (или нет), то почему?

Нерекурсивные ЦФ всегда устойчивые (у них нет знаменателя, точнее он равен 1, следовательно, нет полюсов).

49. Сколько полюсов может иметь передаточная функция нерекурсивного ЦФ?

50. Как преобразовать комплексную передаточную функцию H(jω) к виду A(ω)+ jB(ω), где A(ω) и B(ω) – чисто вещественные выражения?

51. В чём физический смысл модуля и аргумента передаточной функции?

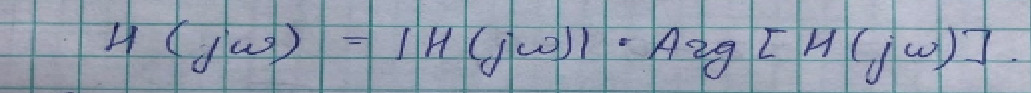
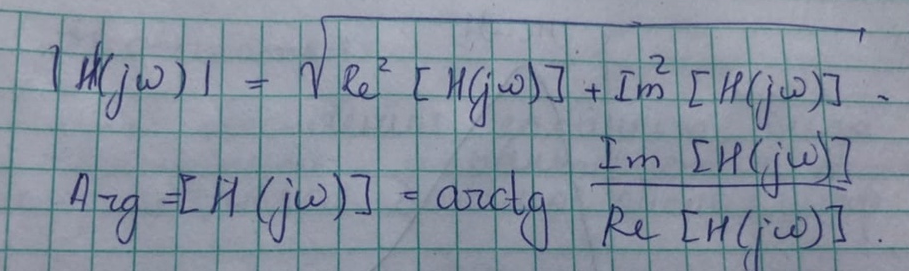
Модуль передаточной функции-АЧХ

Аргумент передаточной функции-ФЧХ

52. Как найти положение нулей и полюсов передаточной функции на комплексной плоскости?

Пример:

53. Как по расположению нулей и полюсов определить модуль и аргумент для заданной частоты?

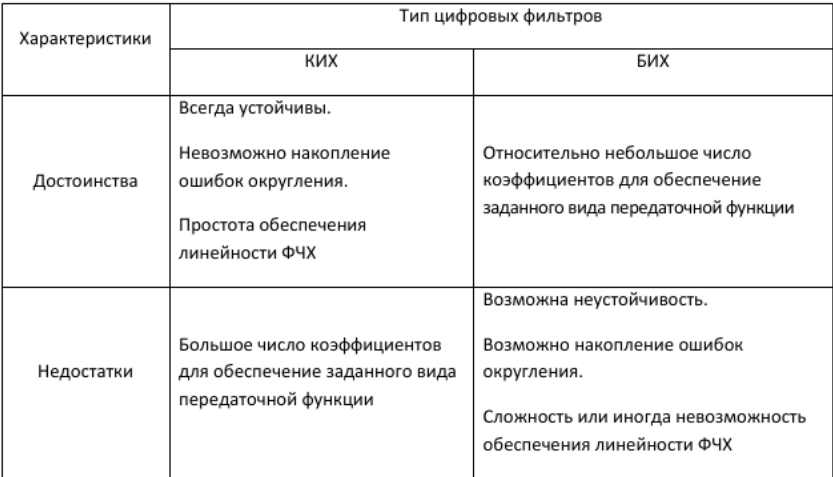
54. В чем преимущества и недостатки нерекурсивных ЦФ по сравнению с рекурсивными?

КИХ-фильтр- нерекурсивный

БИХ-фильтр-рекурсивный

55. В чем преимущества и недостатки рекурсивных ЦФ по сравнению с нерекурсивными?

См. 54

56. Как связаны импульсная характеристика КИХ-фильтра с набором его коэффициентов?

Импульсной характеристикой фильтра называется его отклик на единичный импульс.

Импульсная характеристика КИХ-фильтра повторяет набор его коэффициентов.

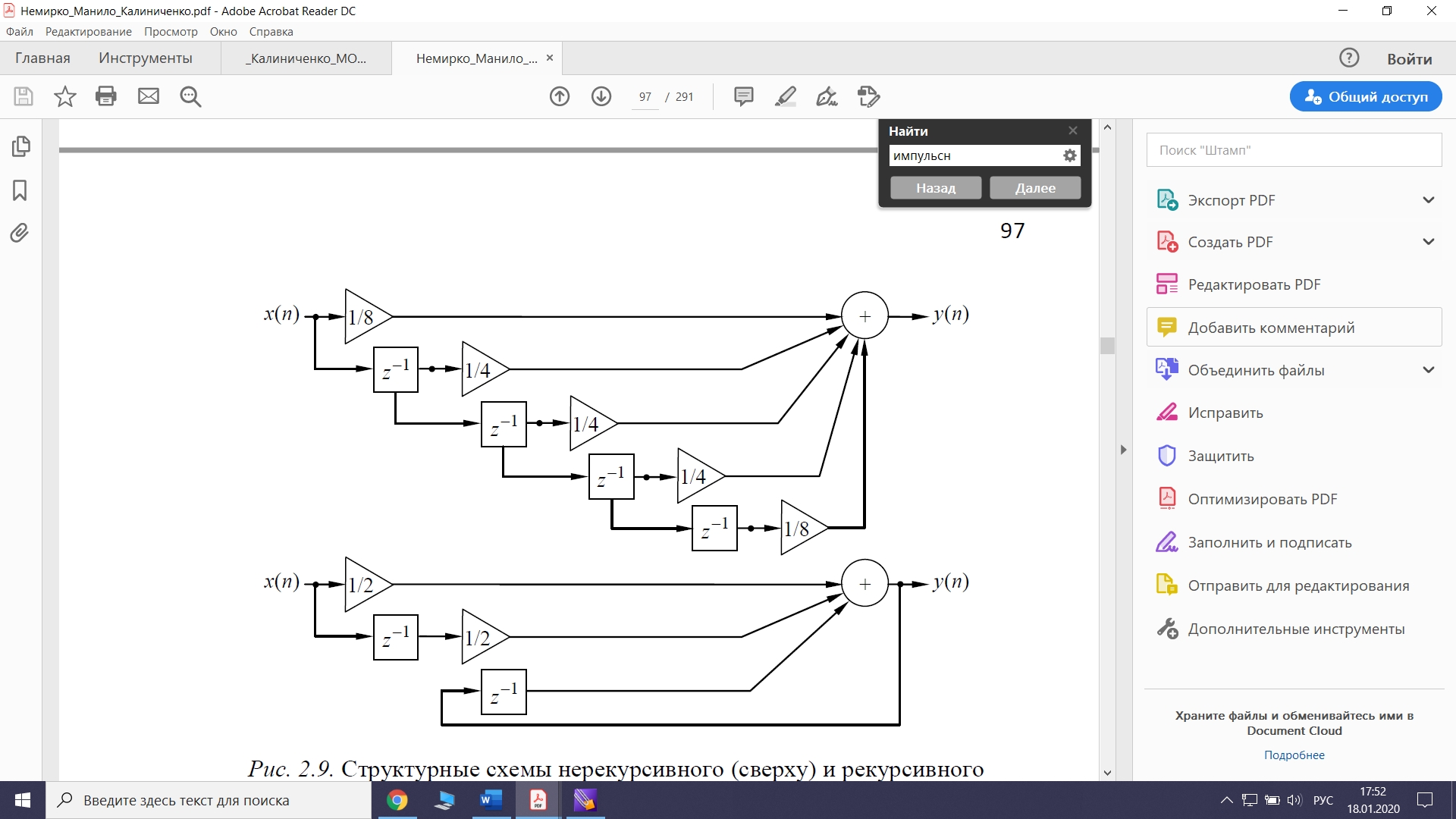
Рис.1 – Структурная схема нерекурсивного фильтра

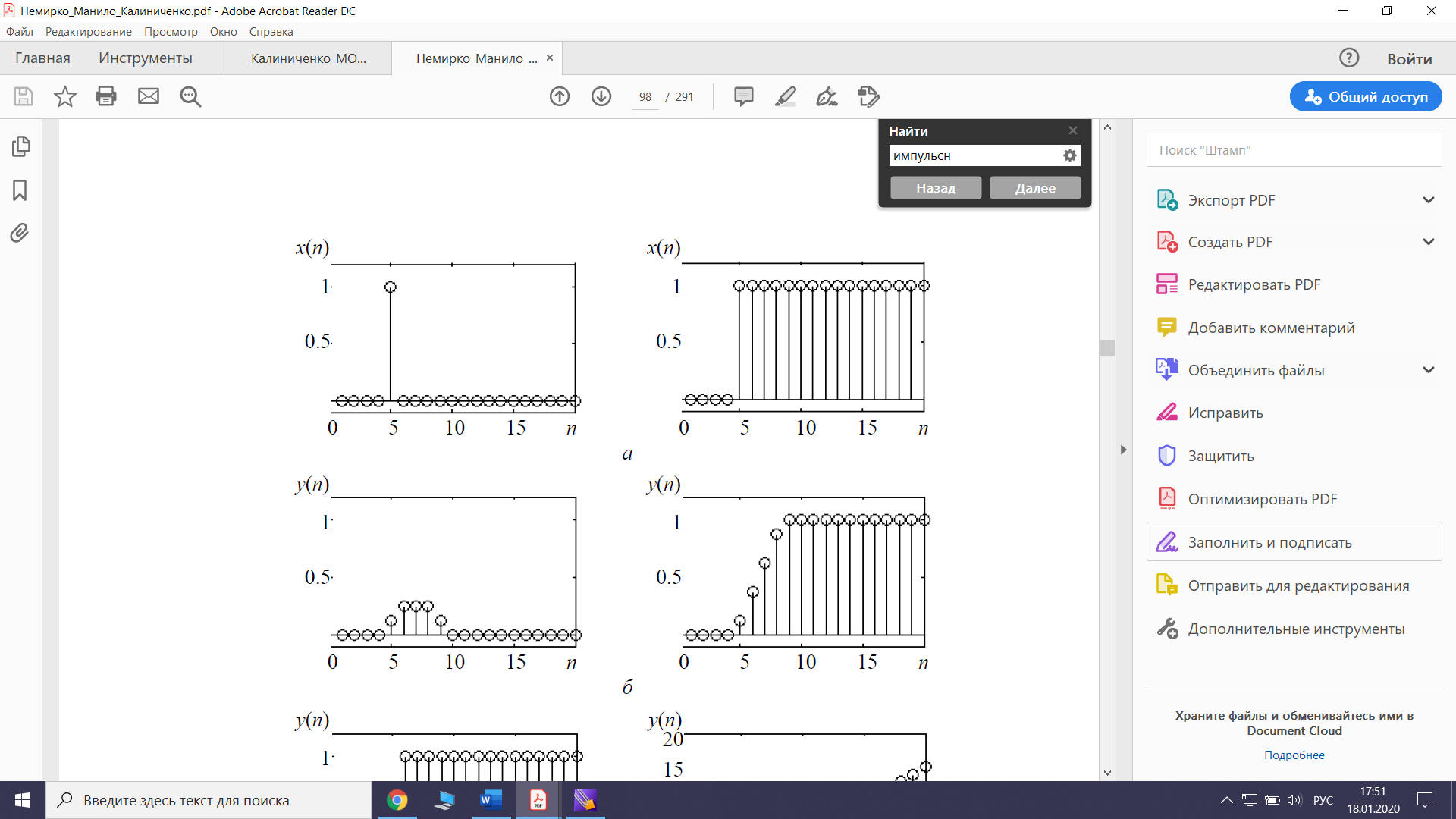
Рис.2 – Единичное импульсное воздействие и импульсная характеристика КИХ-фильтра

57. Выведите выражение для передаточной функции нерекурсивного ЦФ (очень простого), заданного разностным уравнением.

Передаточная функция нерекурсивного ЦФ, полученная в результате применения прямого Z-преобразования к уравнению, имеет вид

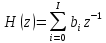
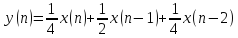
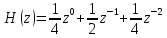
58. В чём заключается физический смысл линейности ФЧХ ЦФ?

Интерес предоставляет длительность и интервалы.

Все частотные составляющие будут задержаны на одно и то же время. Следовательно, все временные соотношения между зубцами остаются постоянными.

Если ФЧХ нелинейная, то задержка воли будет на разное время.

При нелинейной длинна PQ не такая, какая на самом деле. Следовательно, ошибка в постановке диагноза.

59. Почему симметрия коэффициентов нерекурсивного ЦФ приводит к линейности его ФЧХ?

Фильтр получается, когда параметры равны ,  или . Такие параметры приводят к уравнению вида:

(11)

Уравнение (11) выполняется если  при , если  четно, или при , если  нечетно. Наглядно этот случай отображен на рисунке 7.

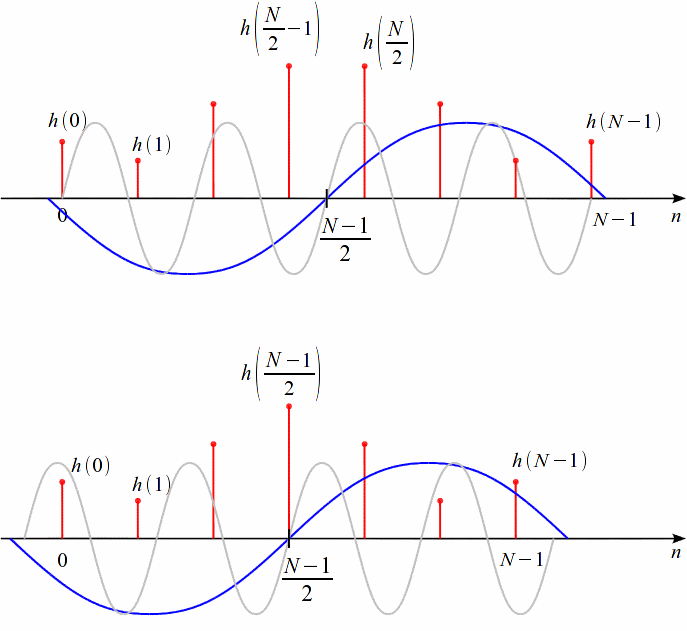Рисунок 7: Фильтр с линейной ФЧХ и симметричной импульсной характеристикой при нечетном и четном порядках фильтра.

Поясним рисунок 7. Параметр  выбран таким образом чтобы синус  всегда имел ноль на оси симметрии, т.е. при . Таким образом получили синус, который антисимметричен относительно оси симметрии фильтра при любой частоте . Тогда если справа и слева от оси симметрии импульсная характеристика будет иметь одинаковые значения, как это показано на рисунке, то (11) будет иметь сумму слагаемых с противоположными знаками, которые взаимно скомпенсируют друг друга и получим фильтр с линейной ФЧХ. Важно отметить, что при четном порядке (нижний график рисунка 7) центральный отсчет импульсной характеристики попадает на ноль синуса и снова получаем фильтр с линейной ФЧХ. Таким образом фильтр с симметричной относительно оси симметрии импульсной характеристикой всегда приводит к линейной ФЧХ.