89. Что такое «быстрое преобразование Фурье» и как оно связано с дискретным преобразованием Фурье?

Быстрым преобразованием Фурье (БПФ) называют набор алгоритмов, реализация которых приводит к существенному уменьшению вычислительной сложности ДПФ. Основная идея БПФ состоит в том, чтобы разбить исходный N-отсчетный сигнал x(n) на два более коротких сигнала, ДПФ которых могут быть скомбинированы таким образом, чтобы получить ДПФ исходного N-отсчетного сигнала.

            Так, если исходный N-отсчетный сигнал разбить на два N/2-отсчетных сигнала, то для вычисления ДПФ каждого из них потребуется около (N/2)² комплексных умножений. Тогда для вычисления искомого N-отсчетного ДПФ потребуется порядка 2(N/2)²=N²/2 комплексных умножений, т.е. вдвое меньше по сравнению с прямым вычислением. Операцию разбиения можно повторить, вычисляя вместо (N/2)-отсчетного ДПФ два (N/4)-отсчетных ДПФ и сокращая тем сасым объем вычислений еще в два раза. Выигрыш в два раза является приблизительным, поскольку не учитывается, каким образом из ДПФ меньшего размера образуется искомое N-отсчетное ДПФ.

90. За счёт чего и какой по величине выигрыш даёт быстрое преобразование Фурье?

Самая трудоёмкая часть ДПФ – вычисление коэффициентов путем перемножений экспонент. При использовании БПФ в этом перемножении можно избавиться от избыточной степени экспоненты и сократить количество расчётов: ДПФ - 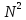, БПФ - .

91. В чём разница между амплитудным спектром, спектром мощности и спектральной плотностью мощности?

Амплитудный спектр показывает значение амплитуд гармоник определенной частоты, составляющих исследуемый сигнал; спектр мощности – мощности этих гармоник. СПМ показывает сколько мощности приходится на единичный интервал частоты .

92. Как будет выглядеть истинный спектр синусоидального сигнала с заданными значениями амплитуды и частоты?

График спектра продолжается на целых частотах, т.е. гармоники будут находиться на частотах , 2, 3, 4… n

93. Что такое гармоники и в чём причина их наличия в спектре сигнала?

Гармоники – гармонические (синусоидальные) состовляющие периодического сигнала разных частот, получаемого суммой этих синусойд.

94. Почему обычно предпочитают пользоваться спектральной плотностью мощности, а не спектром мощности?

Из-за практической удобности. Сама мощность в данном случае является математической мощностью и не несет никакой информации. Важно то, как она проявляется на различных частотах, т.е. как она на них распределена.

95. Почему спектр сигнала рассматривают только в полосе от 0 Гц до частоты Найквиста?

По теореме Котельникова (теорема отсчетов) минимальное значение частоты дискретизации должно удовлетворять:

Если функция, зависящая от времени, имеет ограниченный частотный спектр F, то она полностью определяется дискретными отсчетами ее значений, следующими с частой .

Частота Найквиста – частота, равная половине частоты дискретизации

Диапазон от 0 до часто называется интервалом Найквиста.

Из теоремы Котельникова следует, что полезную информацию будут нести только частоты ниже частоты Найквиста. Частоты выше частоты Найквиста являются зеркальным отображением нижних частот. Если спектр сигнала не имеет составляющих выше частоты Найквиста, то он может быть оцифрован и затем восстановлен без искажений.

96. Что такое разрешение спектра и чем оно определяется?

Спектральное разрешение характеризует способности спектра к различию близких по частоте составляющих.

Оно определяется: частотой дескритизации Fs и количеством отсчётов N:

97. Что называют «спектральной утечкой» и чем она вызывается?

Из-за того, что при использовании ДПФ явно предполагается бесконечное периодическое продолжение анализируемого сигнала, в получаемом спектре может наблюдаться эффект, называемый «спектральной утечкой», который проявляется в «растекании» мощности спектральных составляющих по диапазону частот. Этот эффект может быть снижен при применении сглаживающих окон.

98. Что понимают в спектральном анализе под термином «окно»?

Под «сглаживающими окнами» понимают функции, имеющие на краях близкие к нулю значения, которые плавно возрастают до единицы в средней части функции.

99. Для чего используют сглаживающие окна при спектральном анализе?

В случае использования алгоритма БПФ для получения спектральных оценок возможны два основных варианта:

• Периодограммный метод (расчет БПФ для всего фрагмента сигнала целиком)

• Метод Уэлча (использование усреднения спектров, рассчитанных по перекрывающимся фрагментам сигнала)

При использовании периодограммного метода выполняется следующая последовательность процедур:

1. Удаление из сигнала среднего значения (или линейного тренда) с целью устранения постоянной составляющей

2. Умножение сигнала на сглаживающее окно для уменьшения спектральной утечки, вызываемой разрывами на краях анализируемого фрагмента, возникающими при его периодическом продолжении

3. Дополнение фрагмента сигнала нулями до размера, соответствующего какой-либо степени числа 2, что позволяет далее использовать алгоритм БПФ

4. Расчет дискретного преобразования Фурье с помощью алгоритма БПФ

5. Расчет СПМ и умножение его на корректирующие коэффициенты (имеются формулы, см. методу)

(!) Следует помнить, что применение сглаживающих окон хоть и снижает спектральную утечку, но приводит в то же время к ухудшению спектрального разрешения.

100. Для чего из сигнала перед вычислением оценки спектра устраняют постоянную составляющую?

При использовании периодограммного метода (расчет БПФ для всего фрагмента сигнала целиком)выполняется удаление из сигнала среднего значения (или линейного тренда) с целью устранения постоянной составляющей, которая доминирует в сигнале сердечного ритма, но не несет информации о вариабельности сердечного ритма.

101. Для чего применяют дополнение сигнала нулями?

Дополнение фрагмента сигнала нулями до размера, соответствующего какой-либо целой степени числа «2» позволяет далее использовать алгоритм БПФ.

102. Что такое разрешение спектра?

Разрешение спектра - способность спектра к различению близко расположенных частотных составляющих.

103. Как определить шаг по частоте для спектра, рассчитанного с помощью БПФ?

Шаг по частоте = Частота дискретизации/число точек для алгоритма БПФ

104. Как дополнение нулями влияет на разрешение спектра?

Дополнение сигнала не приводит к улучшению спектрального разрешения, потому что оно выражается в интерполяции значения по частоте.

105. Какой (минимальной) длины фрагмент сигнала нужен для получения (с помощью ДПФ) достоверной спектральной оценки компоненты с заданной частотой?

Интересует сигнал до ½ частоты дискретизации: Заданная частота = Частота дискретизации/число отсчётов => число отсчётов = Частота дискретизации/заданная частота

106. Каким способом получают сигнал сердечного ритма?

ЭКГ

107. Что служит входной информацией для анализа вариабельности сердечного ритма?

Анализ вариабельности сердечного ритма (ВСР) представляет собой метод исследования статистических и частотных свойств сигнала, образуемого последовательностью интервалов времени между смежными сокращениями сердца, относящимися к фоновому ритму. Интервалы времени между последовательными сокращениями сердца (RR-интервалы) обычно измеряются по ЭКГ как расстояния между вершинами R-зубцов QRS-комплексов. Если за период регистрации ЭКГ в сигнале наблюдались нарушения сердечного ритма или помехи, вызвавшие ошибки в определении RR-интервалов, то участки сигнала, соответствующие этим событиям, должны исключаться из процедуры анализа. В связи с этим в общепринятых методиках анализа ВСР в качестве входных данных принято использовать не непосредственно последовательность RR-интервалов, а так называемую последовательность NN-интервалов, т. е. интервалов между смежными QRS-комплексами фонового ритма (или комплексами класса «норма»). Так как анализируемая последовательность интервалов времени не является равномерно дискретизованным сигналом, традиционно используемым при частотном анализе, то к ней нельзя непосредственно применить общепринятые методы цифровой обработки. В связи с этим на первом этапе анализа из последовательности NN-интервалов получают с использованием сплайн-интерполяции равномерно дискретизованный сигнал (рекомендованная частота дискретизации составляет 4 Гц), который рассматривается как описание восстановленной функции управления сердечным ритмом. Именно исследование этой функции, порождающей последовательность регистрируемых RR-интервалов, является предметом анализа ВСР. Последовательность NN-интервалов (или RR-интервалов) часто принято графически отображать в виде ритмограммы (тахограммы), на которой значения интервалов изображаются в виде вертикальных линий, а по оси абсцисс откладываются порядковые номера соответствующих интервалов.

высокая активность в диапазоне LF (LowFrequency, 0,04…0,15 Гц)