6.3. Расширенные критерии Дики - Фуллера

Обратимся опять к статистическим данным о величине валового национального продукта (GNP) в США за период с первого квартала 1947 г. по четвертый квартал 1961 г. В главе 5 мы идентифицировали этот ряд как процесс авторегрессии второго порядка

Xt – 217.740 – 5.222 t = 1.380 (Xt–1 – 217.740 – 5.222(t–1)) –

– 0.630 (Xt–2 – 217.740 – 5.222(t–2)) + εt,

или

Xt = 55.017 + 1.304 t + 1.380 Xt–1 – 0.630Xt–2 + εt .

Как проверить гипотезу о наличии единичного корня в модели авторегрессии, порождающей этот ряд? Ведь в рассмотренных выше критериях Дики – Фуллера проверка такой гипотезы велась в рамках моделей авторегрессии первого порядка. Выход из этого положения оказался достаточно простым.

Рассмотрим статистическую модель

SM: xt = α + βt + a1 xt–1 + a2 xt–2 + …+ ap xt–p + εt .

Путем чисто алгебраических преобразований ее можно преобразовать к виду

(#) xt = α + βt + ρ xt–1 + (θ1 ∆xt–1 + …+ θp–1 ∆xt – p+1 ) + εt ,

где

ρ = a1 + a2 + … + ap , θj = – (aj + 1 + … + ap) . (В примере с GNP такое преобразование дает

xt = 55.017 + 1.304 t + 1.380 Xt–1 – 0.630Xt–1 + 0.630Xt–1 – 0.630Xt–2 + εt = = 55.017 + 1.304 t + 0.750 Xt–1 + 0.630 ∆Xt–1 + εt .)

Если исходить из того, что уравнение a(z) = 0 может иметь только один корень z = 1, а остальные p – 1 корней лежат за пределами единичного круга, то тогда наличие единичного корня равносильно тому, что a1 + a2 + …+ ap = 1, т.е. ρ = 1. (См., например, [Hamilton (1994)].) Таким образом, гипотеза существования единичного корня у процесса AR(p) сводится в этом случае к гипотезе H0: ρ = 1 в преобразованном соотношении (#) . Для проверки этой гипотезы можно пользоваться теми же таблицами Фуллера, только на этот раз используются значения статистики T( ρˆ – 1) и t-отношения для проверки гипотезы ρ = 1, полученные при оценивании

расширенной (augmented) статистической модели (#) (с β и α , равными или не равными нулю). Соответствующие “t-статистики” обозначают обычно ADF (augmented Dickey – Fuller), в отличие от статистики DF, получаемой для модели AR(1).

Для того, чтобы не вычислять самим каждый раз значение t-статистики для гипотезы ρ = 1, можно преобразовать (#) к виду

(# #) ∆xt = α + βt + φ xt–1 + (θ1 ∆xt–1 + …+ θp-1 ∆xt – p+1 ) + εt ,

где φ = ρ – 1, так что гипотеза H0: ρ = 1 в (#) равносильна гипотезе H0: φ = 0 в (# #). В качестве альтернативной к H0: ρ = 1 в (#) выступает гипотеза HA: ρ < 1. При переходе от (#) к (# #)) она преобразуется в гипотезу HA: φ < 0 .

При этом, значение “t-статистики” для проверки гипотезы H0: ρ = 1 в (#) численно равно значению “t-статистики” для проверки гипотезы H0: φ = 0 в (# #).

Пример

Для ряда GNP оценивание модели

∆xt = α + βt + φ xt–1 + θ1 ∆xt–1 + εt

(обычным методом наименьших квадратов) приводит к следующему результату:

www.iet.ru/mipt/2/text/curs_econometrics.htm

Поскольку здесь t = –2.873575 > –3.1744, то гипотеза единичного корня не отвергается даже при выборе 10% уровня значимости. В то же время, статистически незначимыми оказываются коэффициенты при трех последних запаздывающих разностях. P-значение F-статистики критерия для гипотезы о занулении этих трех коэффициентов равно 0.44. Поэтому можно обойтись без трех последних запаздывающих разностей, а такую модель мы только что оценивали, и в ней гипотеза единичного корня была отвергнута.

Критерии Дики - Фуллера фактически предполагают, что наблюдаемый ряд описывается моделью авторегрессии конечного порядка (возможно, с поправкой на детерминированный тренд). Как поступать в случае, когда ряд xt имеет тип ARMA(p,

процесс можно представить в виде процесса авторегрессии бесконечного порядка

c(L) xt = εt ,

где

c(L) xt = a(L) ⁄ b(L) = 1 + с1L + с2L2 + … .

В этом случае представление (# #) с конечным числом запаздываний в правой части заменяется бесконечным представлением

(# # #) ∆xt = α + βt + φ xt – 1 + (θ1 ∆xt – 1 + θ2 ∆xt – 2 + … ) + εt

Однако все коэффициенты последнего невозможно оценить по конечному количеству наблюдений. Как выйти из этого положения?

В работе [Said, Dickey (1984)] было показано, что процесс ARIMA(p, 1, q) с неизвестными p и q можно достаточно хорошо аппроксимировать некоторым

процессом ARI(p*, 1) с p* < 3 T . Это дает возможность ограничиться в правой части (# # #) конечным числом запаздывающих разностей.

6.4. Краткий обзор критериев Дики – Фуллера

Под критерием Дики – Фуллера в действительности понимается группа критериев, объединенных одной идеей, предложенных и изученных в работах [Dickey (1976)], [Fuller (1976)], [Dickey, Fuller (1979)], [Dickey, Fuller (1981)]. В критериях Дики – Фуллера проверяемой (нулевой) является гипотеза о том, что исследуемый ряд xt принадлежит классу DS (DS-гипотеза); альтернативная гипотеза – исследуемый ряд принадлежит классу TS (TS-гипотеза). Критерий Дики – Фуллера фактически предполагает, что наблюдаемый ряд описывается моделью авторегрессии первого порядка (возможно, с поправкой на линейный тренд). Критические значения зависят от того, какая статистическая модель оценивается и какая вероятностная модель в действительности порождает наблюдаемые значения. При этом рассматриваются следующие три пары моделей (SM – статистическая модель, statistical model; DGP –

модель порождения данных, data generating process).

1) Если ряд xt имеет детерминированный линейный тренд (наряду с которым может иметь место и стохастический тренд), то в такой ситуации берется пара

SM: ∆xt =ϕ xt−1 +α +β t +εt , t = 2,…,T ,

www.iet.ru/mipt/2/text/curs_econometrics.htm

DGP: ∆xt =α +εt , t = 2,…,T , α ≠ 0 .

В обоих случаях εt – независимые случайные величины, имеющие одинаковое нормальное распределение с нулевым математическим ожиданием. .

Методом наименьших квадратов оцениваются параметры данной SM и вычисляется значение обычной t-статистики tϕ для проверки гипотезы H0 : ϕ = 0. Полученное значение сравнивается с критическим уровнем tcrit , рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP (случайное блуждание со сносом). DS-гипотеза отвергается, если tϕ < tcrit. Критические уровни, соответствующие выбранным уровням значимости, можно взять из таблиц, приведенных в книгах [Fuller (1976)], [Fuller (1996)], если ряд наблюдается на интервалах длины T = 25, 50, 100, 250, 500. Если количество наблюдений T другое, то тогда можно вычислить приближенные критические значения, используя формулы, приведенные в работе [MacKinnon (1991)].

2) Если ряд xt не имеет детерминированного тренда (но может иметь стохастический

тренд) и имеет ненулевое математическое ожидание, то берется пара

SM: ∆xt =ϕ xt −1 +α +ε t , t = 2,…,T, DGP: ∆xt =ε t , t = 2,…,T .

Методом наименьших квадратов оцениваются параметры данной SM и вычисляется значение t-статистики tϕ для проверки гипотезы H0 : ϕ = 0. Полученное значение сравнивается с критическим уровнем tcrit , рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP (случайное блуждание без сноса). DS-гипотеза отвергается, если tϕ < tcrit . Критические уровни, соответствующие выбранным уровням значимости, можно взять из таблиц, приведенных в книгax [Fuller (1976)], [Fuller (1996)], если ряд наблюдается на интервалах длины T = 25, 50, 100, 250, 500. Если количество наблюдений T другое, то тогда можно вычислить приближенные критические значения, используя формулы, приведенные в работе [MacKinnon (1991)].

3) Наконец, если ряд xt не имеет детерминированного тренда (но может иметь стохастический тренд) и имеет нулевое математическое ожидание, то берется пара

Методом наименьших квадратов оцениваются параметры данной SM и вычисляется значение t-статистики tϕ для проверки гипотезы H0 : ϕ = 0. Полученное значение сравнивается с критическим уровнем tcrit , рассчитанным в предположении, что наблюдаемый ряд в действительности порождается данной моделью DGP (случайное блуждание без сноса). DS-гипотеза отвергается, если tϕ < tcrit . Критические уровни, соответствующие выбранным уровням значимости, можно взять из таблиц, приведенных в книгах [Fuller (1976)], [Fuller (1996)], если ряд наблюдается на интервалах длины T = 25, 50, 100, 250, 500. Если количество наблюдений T другое, то тогда можно вычислить приближенные критические значения, используя формулы, приведенные в работе [MacKinnon (1991)].

Неправильный выбор оцениваемой статистической модели может существенно отразиться на мощности критерия Дики – Фуллера. Например, если наблюдаемый ряд порождается моделью случайного блуждания со сносом, а статистические выводы производятся на основании результатов оценивания статистической модели без включения в ее правую часть трендовой составляющей, то тогда мощность критерия, основанная на статистике tϕ , стремится к нулю с возрастанием количества наблюдений

www.iet.ru/mipt/2/text/curs_econometrics.htm

(см. [Perron (1988)]). С другой стороны, оцениваемая статистическая модель не должна быть и избыточной, поскольку это также ведет к уменьшению мощности критерия.

Формализованная процедура использования критериев Дики – Фуллера с последовательной проверкой возможности редукции статистической модели приведена в работе [Dolado, Jenkinson, Sosvilla – Rivero (1990)]; см. также [Enders (1995)]. Эта процедура будет рассмотрена ниже в разделе 6.6.

Если наблюдаемый ряд описывается моделью авторегрессии a(L) xt = εt более высокого (но конечного) порядка p , уравнение a(z) = 0 имеет не более одного единичного корня и не имеет корней внутри единичного круга, то тогда можно воспользоваться расширенным (augmented) критерием Дики – Фуллера. В каждой из трех рассмотренных выше ситуаций достаточно дополнить правые части оцениваемых статистических моделей запаздывающими разностями ∆xt−j , j = 1, …, p − 1, так что оцениваются расширенные статистические модели

значениями tcrit , что и для нерасширенных моделей. DS-гипотеза отвергается, если tϕ <

tcrit.

Расширенный критерий Дики – Фуллера может применяться и тогда, когда ряд xt описывается смешанной моделью авторегрессии – скользящего среднего. Как было указано в работе [Said, Dickey (1984)], если ряд наблюдений x1,…, xT порождается моделью ARIMA(p, 1, q) c q > 0, то его можно аппроксимировать моделью ARI(p*, 1) =

ARIMA(p*, 1, 0) с p*< 3 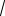T и применять процедуру Дики – Фуллера к этой модели.

Однако даже если ряд наблюдений x1,…, xT действительно порождается моделью авторегрессии AR(p) конечного порядка p, то значение p обычно не известно, и его приходится оценивать на основании имеющихся наблюдений, а такое предварительное оценивание влияет на характеристики критерия. Поэтому при анализе данных приходится сначала выбирать значение p=pmax достаточно большим, так чтобы оно было не меньше истинного порядка p0 авторегрессионной модели, описывающей ряд, или порядка р* аппроксимирующей авторегрессионной модели, а затем пытаться понизить используемое значение р, апеллируя к наблюдениям.

Такое понижение может осуществляться, например, путем последовательной редукции расширенной модели за счет исключения из нее незначимых (на 10% уровне) запаздывающих разностей (GS-стратегия перехода от общего к частному) или путем сравнения (оцененных) полной и редуцированных моделей с различными р ≤ pmax по информационному критерию Шварца (SIC). В работах [Hall (1994)] и [Ng, Perron

(1995)] показано, что если pmax ≥ p0 , то тогда в пределе (при Т → ∞) SIC выбирает правильный порядок модели, а стратегия GS выбирает модель с р ≥ р0 ; при этом факт определения порядка модели на основании имеющихся данных не влияет на асимптотическое распределение статистики Дики -– Фуллера. Таблицы критических

www.iet.ru/mipt/2/text/curs_econometrics.htm