Добавил:

Teana Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Таврический Национальный Университет им. В.И. Вернадского

Предмет:

Экономика

Файл:

Основы страховой (актуарной) математики - Г.М.Кошкин

.pdf

Скачиваний:

Добавлен:

24.05.2014

Размер:

634.88 Кб

Скачать

☆

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Покажем, что для первого слагаемого в правой части (6.9.4) выполняются все условия двумерной центральной предельной теоремы в схеме серий (см. приложение 4, теорема 6П). Пусть

j;N

pNhN

(x) ;

j;N

phN

x Xj

Таким образом

j;N :

fN (x) EfN (x) = pNhN j=1 j;N ;

sN (x) EsN (x) = pNhN =1

2) теоремыОчевидно,6П.чтоДляEэтого( ; необходимо) = (0; 0)показать,.Проверимчтовыполнение условия

j;N j;N

j;N

j;N k

NhN

;

x Xj

Учитывая.6.8),(6 получаем:результаты лемм о дисперсиях оценок sfN (x) è fN (x) (6.4.1),

	E k j;N ; j;N k2 N C1		1	K2		(u)du + N C2 < 1;
	E k j;N ; j;N k2 N C1	Z		K2		(u)du + N C2 < 1;
	1						hN
		1
здесьПо леммe 6.9.1			константы.
0	C1; C2 < 1 некоторые				T	( 1;N ; 1;N ) = :
	lim NE ( 1;N ; 1;N )					( 1;N ; 1;N ) = :		является до-
Проверим выполнение условия Линдеберга, которое								является до-
	N!1

статочным условием применимости центральной предельной теоремы в схеме серий. Для любого > 0 имеем

N = NE k 1;N ; 1;N k2 ; k 1;N ; 1;N k > <

; 1;N k3 =

E k 1;N

E 12;N

+ 12;N

3=2

hE j 1;N j3

+ E j 1;N j3i =

(NhN )3=2

x X1

E K x X1

+h3 E

(

)

(NhN )1=2

"hN

E K

+ h3 E3f (x) +

x X

N (

+h2 E

+ E3

Далее, так как ядра K( ); S( ) ограничены на R1, òî

1
N = O	p		! 0
		NhN
теоремепри N !6Ï1получаем,т.е. условиетребуемыйЛиндебергарезультатвыполняется,. следовательно, по

Теорема 6.9.1 доказана. Введем обозначения:

xN = (xN1; : : : ; xNs) векторная статистика с компонентами xNj =

функция				;
xNj(x) = xNj(t; X1; : : : ; XN ); j = 1; s
H	(1)		H(z) : Rs ! R1;
		(z) = rH(z) = (H1(z); : : : ; Hs(z)) ; Hj(z) = @H(z)=@zj;

возрастающаяN положительнаяс ростом числовая последовательность, неограниченно

торая,=например,(x) = ( может(x); : : :áûòü; (xматематическим)) ограниченнаяожиданиемвектор-функция,статистикико-

1 s

xN .Теперь, согласно теоремам 6.9.1 и 3П можно найти предельное распределение оценки функции интенсивности.

Теорема 6.9.2 (асимптотическая нормальность

N ). Если выпол-

нены условия теоремы 6.9.1 и

(x); s(x) 6= 0; òî

80;

(x)RR1

K2(u)du

NhN

( N (x)

(x)) =

(6.9.5)

s(x)

) N

;

Д о к а з а т е л ь с т в о. В обозначениях теоремы 3П (см. приложение 4) имеем:p xN1 fN

dN = NhN ; N = H(xN ) = H (xN1; xN2) = xN2 = sfN ;

è jp â (Ï.1) (ñì.

= H( ) = H ( 1; 2) = 1 = f ;2 s

H(1)( ) =	2	; 22			=	s	; s2		; 1 = 2 = 0; =
	1		1			1		f

(матрица После подстановкиопределенанайденныхв (6.9.1)).величин

H(1)( ),

приложение 4) приходим к утверждению теоремы. j

Теорема 6.9.2 доказана.

Замечание 6.9.1 По аналогии с теоремой 6.9.2 в работе [33] показана асимптотическая нормальность непараметрических оценок функции интенсивности вида: N;2(x) = fN (x)= (1 FN;2(x)) ; ãäå fN (x) =

fN (x; hN ) (оценка плотности fN (x) определена согласно (6.6.2) данной

x
работы), FN;2(x) = Z0	fN (t; aN )dt.

6.10 Интервальное оценивание функции интенсивности

Результат теоремы 6.9.2 позволяет найти преобразование оценки функциимальноеинтенсивностираспределение(.xНам), котороепотребуетсяимеетследующеепредельноепростоестандартноеобобщениенор-

результата из [34], которое приведено в приложении 4 в виде теоре-
ìû 4Ï.						fTN ;	N = 1; 2; : : :g последова-
тельностьВтеореместатистик4П показано,такая, чточто, если
вая последовательность			p		[	TN	] =	0; 2( )	; число-
				q
			qN " 1, òîN				) N1
p		[g (TN ) g( )] =) N1 n0; [g0( ) ( )]2o;							(6.10.1)
	qN
гдеСогласноg функция,[34, стримеющая.377], функциюпервую производную и g0( ) = 0.
								6
					g следует выбирать так, чтобы
			g0( ) ( ) = c;						(6.10.2)

стикигде c не зависит от . В этом случае асимптотическая дисперсия стати- g(TN ) не будет зависеть от .

Функцию g найдем из уравнения g = Z	( ): В нашем случае, учи-
	cd

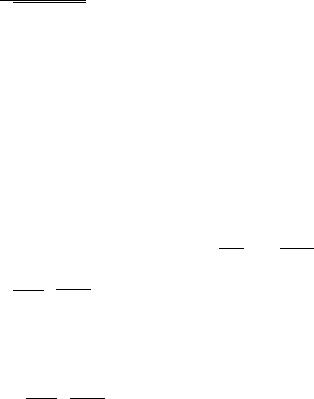
тывая (6.9.5), имеем

( p

g =

s(x)d (x)

cd (x)

(6.10.3)

( )

qRR

K2(u)du

(x)

НайдемИз (6.10.преобразование3)следует, что gоценки(x) = p

функцииx:

интенсивности, имеющее

предельное стандартное нормальное распределение.

Теоремà 6.10.1 .

В условиях теоремы 6.9.2

pNh

N ps(x)

N (x)

(x)

=) N1 f0; 1g :

(6.10.4)

R K2(u)du hp

Д о к а з а т е л ь с т в о. В обозначениях теоремû 4П, полагая:

qN = NhN ; TN = N ; = g( ) =

1 K2(u)du

g0( N ) ( N ) =

;

2ps(x)

получаем утверждение 6.10.4.

Теорема 6.10.1 доказана.

O(aN )

è,

Учитывая,

÷òî jb (sN (x))j =

(ñì.

лемму

6.3.3)

â !1

psN (x)

разом, при выполнении условий теоремы 6.9.2

íà

ps(x)

n 1=2

lim aN NhN = 0 (условие 6) теоремы 6.9.1), взяв

aN = o

формуле (6.10.4) правомерно заменить

f Таким об-

sN (x)

(x)i

N (x)

=) N1 f0; 1g :

(6.10.5)

K (u)du

s R

На основе утверждения (6.10.5) можно построить интервальную оценку заданной надежности (1 ) для функции интенсивности (x):

sN (x)

(x)

N (x)

< U1 =2;

(6.10.6)

K (u)du

ãäå U

1 =2

квантиль уровня

стандартного нормального распре-

деления. Таким образом

1 K2

(u)du

< (x) <

N (x)

2pNhN sN (x)

1 K2

(u)du

(x)

(6.10.7)

2pNhN sN (x)

Достоинством интервальной оценки (6.10.7) является то, что она определяется через известные функции (сравните с дисперсией предельногоИнтервальныераспределениянепараметрическиеоценки (x)). оценки (6.10.7) рассмотрены в ра-

ботах [35] [38], [39], [40].

6.11 Сходимость в среднеквадратическом оценок функции интенсивности

Одной из основных точностных характеристик оценки является ее среднеквадратическое отклонение (СКО) от истинного значения. При словленныенахожденииихСКОвозможнойоценки подстановкинеограниченностью,(x) возникаютнапример,трудности,когда оценкиобу-

знаменателей принимают значения, равные нулю. Решение этой проблемы состоит либо в использовании усеченных модификаций оценокN (x) [32], либо их кусочно-гладких аппроксимаций [42], [43]:

( N ; ) = e (x; ) =	N (x)
		;	(6.11.1)
	[1 + j N (x)j ]

гдеВ данной> 0; >работе0; рассмотрим1; > 0: кусочно-гладкие аппроксимации (6.11.1)

нормыВведемотклоненияобозначения:оценкиM kyN k = E kyN k момент порядка для тройки yN (x) от функции (x) в точке x. Введем

( ; k; m), ãäå k; m натуральные числа, множество

T (m) = f( ; k) : (m) = 2k=(m k 1) > 0; m m0 = [3; k = 1; 2k; k 2]g.

потребуется следствие 4

Для нахождения СКО оценок (r); r

из [43], которое приведено в приложенииN 4 в виде теоремы 5П.

Чтобы использовать формулу (П.2) приложения 4 для определения димо,главныхсогласночастей условиюСКО кусочно2) теоремы-гладких5Ï,аппроксимацийзнать порядокeсходимости(x; ), необхок-

таты приводятся ниже в виде лемм 6.11.1 и 6.sfN (x); fN (x)	. Эти резуль-
нулю четвертого момента отклонения оценок 11.2.

Лемма 6.11.1 . Если выполнены условия леммы 6.3.3 и

aN = o N 1=2 ;

òî ïðè N ! 1

M4 ksN	(x)k = E (sN (x) s(x))4	= O N 2 :	(6.11.2)
f	f

Д о к а з а т е л ь с т в о. Представим

E (sN (x) s(x))4 = E [(sN (x) EsN (x)) + b (sN (x))]4 :

Привлекая при

неравенство

p = 4 è m = 2f

m !p

jaij

mp 1

jaijp; p > 1;

имеем

i=1

E (sN (x) s(x))4 23 hE (sN (x) EsN (x))4 + b4 (sN (x))i4

b (sN (x))

Согласно лемме 6.3.3

= O (a

значит b4 (s

(x)) = o

Согласно [44]

E FN (x) EFN (x)

= O N 2

; следовательно

E (sN (x)

EsN

(x)) = O N

;

ливость соотношения (6.11.2).

отсюда немедленно следует справед-

Лемма 6.11.1 доказана.

Найдем порядок сходимости четвертого момента отклонения оценок fN (x) от истинной кривой смертей f(x).

Лемма 6.11.2 . Пусть выполняются условèÿ :

1) f(x) 2 N2;1(R); 2) sup f(m)(x) < 1; m = 0; 2;

x2R1

3) ÿäðî K(u) 2 A2; 4) ïðè x ! 1 : 1 K(x) = o x 2 ;

N!1 N	NhN
5) lim h +	1	= 0;
5) lim h +		= 0;
Тогда при N ! 1			NhN			!
M4 kfN (x)k = E (fN (x) f(x))4 = O			NhN		+ hN4	!	: (6.11.3)
				1		2
				1

Д о к а з а т е л ь с т в о. Рассуждая, как при доказательстве леммы 6.11.1, и учитывая, что в силу леммы 2.3.3 [32] E (fN (x) f(x))4 =

O (NhN ) 2 ; согласно лемме 6.6.4 при = 2 :

b (f (x)) = O h2 , получаем выражение (6.11.3). NЛемма 6.11.2Nдоказана.

Теперь, используя теорему 5П приложения 4, найдем СКО кусочногладких аппроксимаций ( N ; ).

Теорема 6.11.1 . Пусть выполнены следующие условия: 1) (x) 6=

0; s(x) 6= 0; 2) выполнены условия лемм 6.11.1 и 6.11.2; 3) =	NhN + hN4
	1
Тогда для любых ( ; 2) 2 T (m) ïðè N ! 1:

E [ ( N ; )

(x)]2

(x)

1 (K(u))2 du

s(x)NhN

2h4

f(2)(x)

= O

+ hN4

3=2

(6.11.4)

4 N

s2(x)

NhN

Ä î ê à ç à ò å ë ü ñ ò â

о. Покажем справедливость соотноше-

ния (6.11.4). В обозначениях теоремы 5П (см. приложение 4) имеем:

s = 2; z = (z1

; z2) ; H(z) = z1

=z2; yN

= (y1N ; y2N ) = (fN ; sN ) ; =

4 и покажем, что M4

; sN

= O

d 2

. Это сразу следуетf

( 1; 2) = (f(x); s(x)) ; dN

= O

NhN

+ h 4

; k = 2. Возьмем m = m0 =

ношения (6.11.2), соотношения

M4 kfN ; sN k

2 [M4 fN + M4 sN ]

(6.11.3) и неравенства

k k

s(kx) = 0, à ïðè z2 = 0 функция

Далее, так как

z1=z2 2 N2;2 (f(x); s(x)) ;

то все условия теоремы 5П выполнены для ( N ; ) = ( N ; ) ïðè

0 = 4: Теорема 6.11.1 доказана. 97

PN (A).

6.12 Контрольные задания

Задание 6.11.1

Докажите свойства 1) 6) из п.6.1 для оценки вероятности

Задание 6.11.2

Сформулируйте гипотезу о методе получения аппроксимации вероятности q

Ваших предположенийx в таблице смертности.Приведитеиз примерПриложениясмещенной1. Дайтеоценкиобоснованиевероят-

ности с меньшей среднеквадратической ошибкой, чем дисперсия несмещенной оценки.

Задание 6.11.3

Опишите организацию однородной серии опытов для получения оценок вероятностей tqx; tpx;px; tjuqx; tjqx:

Задание 6.11.4

По 5 числам, взятым из таблицы равномерно распределенных слу- чайных чисел [41, с. 426], постройте эмпирические функцию распределения и функцию выживания. Сравните с теоретическими кривыми. В качестве 5 чисел можете взять 10, 9, 73, 25, 33.

Задание 6.11.5

В условиях Задания 6.11.4 постройте гладкие эмпирические функцию распределения и функцию выживания. В качестве базовых функций распределения F(u) (ядер) можно взять:

равномерная функция распределения

F	8	2	+ u;		2	1		2
	<	1	0;	u	1	21	;	1	;
	<		1;	u >		2 ;
	(u) =					< u

функция распределения Коши

1			1
F(u) =		+			arctgu;		1 < u < 1;
	2
логистическая функция распределения
F(u) =			1			; 1 < u < 1;

			1 + e u
гиперболический косинус
F(u) = 1			2	arctge u;			1 < u < 1;


			98

двойной показательный закон

F(u) = e e u ; 1 < u < 1;

Задание 6.11.6

Синтезируйте наилучшие смещенные оценки функций распределения и выживания в точке x.

Задание 6.11.7

На основе гладкой эмпирической функции распределения с ядрами Задания 6.11.5 по выборке Задания 6.11.4 постройте ядерные оценки плотности распределения. Вычислите значения оценки плотности и ее дисперсию в точках 0, 50, 100.

Задание 6.11.8

В условиях Задания 6.11.7 постройте алгоритм нахождения эмпири- ческого параметра размытости методом максимума правдоподобия.

Литература

[1]Bowers N.L., Gerber H.U., Hickman J.C., Jones D.A., Nesbitt C.J. Actuarial Mathematics. Itasca, Illinois: The Society of Actuaries, 1986, 624 p.

[2]Фалин Г.И., Фалин А.И. Введение в актуарную математику. М.: Èçä-âî ÌÃÓ, 1994, 86 ñ.

[3]Фалин Г.И. Математический анализ рисков в страховании. М.: Российский юридический издательский дом, 1994, 130 с.

[4]Гербер Х. Математика страхования жизни. М., Мир, 1995, 154 с.

[5]Четыркин Е.М. Пенсионные фонды. Зарубежный опыт для оте- чественных предприятий, актуарные расчеты. М.: АО "АРГО", 1993, 100 с.

[6]Штрауб Э. Актуарная математика имущественного страхования. М., Мир, 1988, 146 с.

[7]Колемаев В.А., Калинина В.Н. Теория вероятностей и математи- ческая статистика. М.: Инфра-М, 1997, 302 с.

[8]Боровков А.А. Теория вероятностей. М.: Наука, 1986, 432 с.

[9]Боровков А.А. Математическая статистика. Оценка параметров. Проверка гипотез. М.: Наука, 1984, 472 с.

[10]Боровков А.А. Математическая статистика. Новосибирск: Наука; Изд-во Института математики. 1997, 772 с.

[11]Виленкин С.Я. Статистическая обработка результатов исследования случайных функций. М.: Энергия, 1979. 320 с.

100

<<< < Предыдущая 1 2 3 4 5 6 7 8 910 / 1210 11 12 > Следующая >>>

Соседние файлы в предмете Экономика

#
24.05.20141.83 Mб5761Основы рекламы - Антипов К.В..doc
#
24.05.20145.93 Mб255Основы рекламы - Мудров А.Н..doc
#
24.05.2014844.09 Кб38Основы рыночного ценообразования - Шеховцева Л.С.pdf
#
24.05.2014278.55 Кб34Основы рыночной экономики - Марголин Ф.Б. и др..pdf
#
24.05.20141.35 Mб230Основы статистики - Кошевой О.С..pdf
#
24.05.2014634.88 Кб62Основы страховой (актуарной) математики - Г.М.Кошкин.pdf
#
24.05.20142.01 Mб53Основы страховой деятельности - Грищенко Н.Б..pdf
#
24.05.20142.01 Mб145Основы страховой деятельности - Грищенко Н.Б.pdf
#
24.05.20141.21 Mб201Основы теории коммуникации - Николаева Ж.В..pdf
#
24.05.2014234.36 Кб54Основы теории коммуникации - Шпаковская С.В., Шпаковский В.О..pdf
#
24.05.201419.75 Mб38Основы управления финансами - Ван Хорн Дж. К..pdf