§43. Лінійні та кутові перемішення при згині.

В результаті згину вісь балки скривлюється. Це значить, що точки, які лежать на ній, тобто перерізи балки, отримують деякі переміщення. Так як деформації малі у порівнянні з розмірами балки, то будемо вважати, що переміщення перпендикулярні початковому положенню балки. Крива лінія, якою стає початкова вісь балки, називається зігнутою віссю балки, або пружною лінією (рис. 86). Вертикальні переміщення перерізів будемо називати прогинами. Прогини в різних точках балки різні, і залежать від відстані z від прийнятого початку координат, тобто y_z = f(z). При z = 0 y_z = 0, а при z = він досягає свого найбільшого значення y_max. Найбільший прогин будемо позначати буквою f, тоді y_max = f.

Осі координат домовимося розміщувати таким чином.

Початок координат приймемо на лівому кінці балки, вісь z направимо вправо по осі балки, а вісь у - вверх. Таке розміщенння осей дасть можливість рахувати прогини балки вниз відємними, а прогини вверх - додатніми.

Рис. 86

Кут, що утворює дотична до довільної точки К зігнутої осі з початковим її положенням, умовимося позначати буквою . Цей кут виражає кутове переміщення поперечного перерізу балки при згині і називається кутом повороту перерізу балки. Остаточно: у - лінійне переміщення перерізу балки,  - кутове переміщення.

В багатьох випадках прийняті перерізи балок із умови міцності мають досить великі прогини, що не відповідають нормам проектування. В цьому випадку необхідний поперечний переріз визначають із умови жорсткості. Крім розрахунку балок та інших консрукцій на жорсткість, вивчення деформацій балок необхідне ще для розвязку статично невизначених задач при згині, коли потрібно додатково до рівнянь статики складати рівняння із умови деформації осі балки.

§44. Визначення переміщень методом початкових параметрів.

Для визначення зігнутої осі балки необхідно скласти її рівняння, тобто виразити ординати (прогини балок) в функції від положення точок по довжині балки, іншими словами, щоб знайти залежність у = f(z). Щоб знайти цю залежність, використаємо рівність (81), що отримана при доведенні формули нормальних напруг при згині та виражає залежність кривизни балки із згинальним моментом та поперечною жорсткістю перерізу.

Формула кривизни з вищої математики виражає її звязок з похідними у та у від ординати кривої:

.

Залежність цю можна спростити, маючи на увазі, що прогини балок дуже малі в порівнянні з довжиною балки, а кути нахилу перерізів не перевищують 1. В знаменник правої частини цієї формули входить (у)² - тангенс кута нахилу в квадраті, що є малою величиною у порівнянні з другою величиною, що входить в двочлен знаменника, а тому її відкидають, в результаті чого формула приймає вигляд

,

тобто кривизна балки наближено дорівнює другій похідній від прогину. Тепер формулу можна представити так:

Нагадаємо з математики, що знак другої похідної залежить від напрямку осей координат, а саме: якщо вісь у направлена вверх, а випуклість осі направлена вниз, то знак другої похідної буде додатнім, тоді:

(98)

Отримане рівняння (98) називається наближеним диференційним рівнянням зігнутої осі балки.

Існує декілька методів розвязку цього рівняння, один з яких - метод початкових параметрів.

Академіком М.М. Криловим було розвязане це рівняння для балки, що завантажена всіма видами навантажень. В результаті їм було отримано універсальне рівняння пружної лінії, що має слідуючий вид (у формі, запропонованій професором А. П. Коробовим):

^{za zb zc}1 ^zc2

Це рівняння ми подаємо для випадку рівномірно розподіленого навантаження. Тут у₀, ₀, М₀ і Q₀ - початкові параметри: у₀ - прогин на початку координат; ₀ - кут повороту початкового перерізу; М₀ - згинальний момент в початковому перерізі; Q₀ - поперечна сила в тому ж перерізі. Відмітимо, що у₀ і ₀ - це геометричні фактори, а М₀ та Q₀ - силові фактори.

Рис. 87

Початкові параметри у₀, ₀, М₀ і Q₀ можуть приймати яке завгодно значення: додатні, відємні та дорівнювати нулю. Визначають ці чотири величини, виходячи із умови закріплення балки, а також навантаження лівого кінця, що прийнятий за початок координат. На рис. 87 всі початкові параметри - додатні: у₀ - відкладений вверх від осі z; ₀ - поворот перерізу, припускається, що проти годинникової стрілки; М₀ - направлений за годинниковою стрілкою; Q₀ - направлена вверх. Що стосується інших доданків у рівнянні методу початкових параметрів, то їх знак визначається у залежності від того, чи створює дане навантаження додатній або відємний згинальний момент в перерізі з абсцисою z. Знак (переривач) показує, що

^za

відповідний доданок потрібно врахувати тільки при zа. Це значить, що при визначенні прогину в якомусь перерізі з координатою z в рівняння входять лише ті навантаження, що лежать зліва від цього перерізу.

Отже, універсальне рівняння прогинів містить у собі слідуючі доданки:

а) чотири - для початкових параметрів;

б) одне - для зовнішніх моментів;

в) одне - для зосереджених сил;

г) два - для рівномірно розподіленого навантаження.

Замітимо, що всі доданки, крім початкових параметрів, знаходяться під знаком суми, що розповсюджується на всі навантаження даного виду. В такому вигляді універсальне рівняння прогинів рекомендується до практичного використання (і до запамятовування.). Рівняння кутів повороту може бути легко отримане із рівняння прогинів шляхом обчислення похідної по координаті z.

Приклад 26. Для балки (рис. 88,а) підібрати двотавровий переріз та побудувати епюри кутів повороту перерізів і прогинів. Е = 210⁵ МПа,  = 160 МПа,  = 100 МПа. Власну вагу балки не враховувати.

Розвязок. Знайдемо опорні реакції балки.

1. М_А = 0; q31,5 - V_B6 = 0

2. M_B = 0; V_A6 - q34,5 = 0

Із (1) знаходимо

кН.

Із (2) знаходимо

кН.

Перевірка:

Y_i = V_A+ V_B - q3 = 22,5 + 7,5 - 103 = 0.

Будуємо епюру Q (рис 88,б),

Q_A = V_A = 22,5 кН; Q_C = -V_B = -7,5 кН; Q_B = -V_B = -7,5 кН.

Будуємо епюру М_х (рис 88, в)

М_А = 0; М_С = V_B3 = 7,53 = 22,5 кНм; M_B = 0.

Поперечна сила в перерізі на відстані z від лівої опори дорівнює нулю. Знайдемо z.

Q_z = V_A - qz = 0, звідси м,

тоді згинальний момент в цьому перерізі

кНм.

Рис. 88

Підбираємо двотавровий переріз із розрахунку на міцність по нормальним напругам за формулою (91)

;

М_max= 25,31 кНм = 2531 кНсм.

 = 160 МПа = 16 кН/см².

см³. За таблицями сортаменту приймаємо двотавр № 18а з W_x = 159см³. Перевіримо переріз за дотичними напругами за формулою (93)

де Q_max = 22,5 кН, S_x^відс = 89,8 см² I_x = 1430см⁴, b = 0,51 см,

 = 100МПа = 10 кН/см².

кН/см²   = 10 кН/см²

Умова міцності виконується.

Для даної балки рівняння пружної лінії має вигляд

^z3

Початкові параметри:

у₀ = 0; ;

М₀ = 0; ;

З врахуванням значень рівняння запишеться так:

^z3

або

^z3

Знайдемо ₀ із умови, що прогин правого кінця балки дорівнює нулю, тобто при z = 6 м.

Звідси

Рівняння зігнутої осі балки прийме вигляд:

^z3

Звідси легко отримати рівняння кутів повороту перерізів

^z3

Надаючи абсцисі z різні значення, наприклад для точок А, Д, С, Е, В (рис 88,а), побудуємо епюру  при Е = 210⁵ МПа = 210⁴ кН/см², I_x = 1430см⁴.

При z = 0

рад

При z = 1,5 м

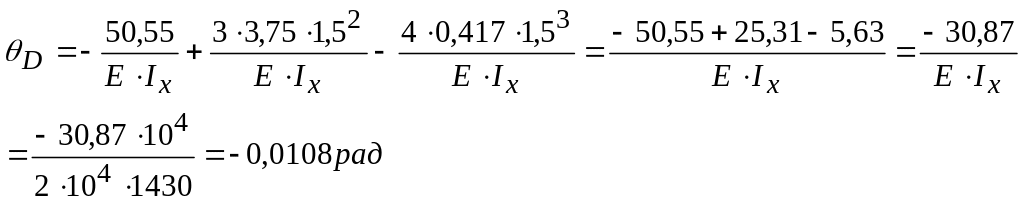
При z = 3 м

При z = 4,5м

рад

При z = 6м

рад.

Відкладаємо додатні значення кутів повороту від осі z вверх. Будуємо епюру кутів повороту (рис. 88, г).

Будуємо епюру прогинів, надаючи абсцисі z значення характерних точок

z = 0 у_А = 0

z=1,5м

z = 3 м

z = 4,5м

z = 6 м у_в = 0.

Відкладаючи віповідні значення в характерних точках, будуємо епюру прогинів (рис. 88, д).

Треба відмітити, що в розглянутому прикладі прогин посередині прольоту дуже мало відрізняється від максимального (приблизно на 1%). Цей результат є в значній мірі загальним - максимальний прогин двохопорної балки без консолей при навантаженнях, що викликають однозначні прогини, мало відрізняється від прогину посередині балки. Тому у вказаних випадках для спрощення розрахунків на жорсткість прогин посередині прольоту приймають за максимальний.

Більш загальний метод визначення переміщень, який можна застосувати для любої лінійно деформованої системи при довільному навантаженні, розроблений німецьким вченим О.Мором. Для зясування суті цього методу необхідно познайомитися з поняттями потенційної енергії деформації при згині і повязаних з нею теорем про роботу зовнішніх та внутрішніх сил, виклад яких наводимо в слідуючих параграфах.