§34. Поперечна сила та згинальний момент

В даному параграфі ми детально познайомимося з поняттям “поперечна сила” і “згинальний момент”, сформулюємо визначення цих понять та правила визначення їх значень.

Нехай балка АВ, що вільно лежить на двох опорах, знаходиться під дією двох сил F₁ та F₂, розміщених в головній площині бруса (рис. 62, а). Відкинувши опори та замінивши їх опорними реакціями V_A i V_B, будемо розглядати балку, що знаходиться під дією сил F₁, F₂, V_A i V_B. Ці сили викликають в перерізах балки внутрішні сили пружності, які визначимо за допомогою методу перерізів.

Рис. 62

Перерізом 1-1 на відстані z від лівої опори розріжемо балку на дві частини, відкинувши праву частину, розглянемо рівновагу залишеної лівої частини (рис. 62, б). Очевидно, що залишена частина балки буде знаходитись в рівновазі під дією зовнішніх сил V_A i F₁ та внутрішніх сил в перерізі 1-1, що замінюють дію відкинутої правої частини балки на ліву. За умовою рівноваги внутрішні сили в перерізі 1-1 обох частин балки будуть рівними за величиною та протилежні за напрямком.

Замінимо дію відкинутої правої частини балки на ліву внутрішніми силами, рівнодіюча яких повинна лежати в площині дії зонішніх сил V_A i F₁. Проекцію цієї рівнодіючої на вісь у позначимо через Q_y, а її момент відносно центру ваги перерізу 1-1 – через М_х, так як ліва і права частини балки знаходяться в рівновазі, то умова рівноваги для них повинна виконуватися. Тобто У_і = 0 і М₀ = 0. За центр моментів приймаємо центр ваги перерізу (точка О).

У_і = V_A - F₁ - Q_y = 0;  М₀ = V_Az – F₁(z – a) – M_x = 0,

звідси

Q_y = V_A - F₁; M_x = V_Az - F₁(z - a).

Таким чином, внутрішні сили в перерізі виявилися приведеними до сили Q_y та пари сил з моментом M_x. Тобто поперечна сила - це проекція рівнодіючої внутрішніх сил на вісь, що перпенидкулярна до осі балки та позначається Q_y або Q. Згинальний момент в довільному перерізі – це момент рівнодіючої внутрішніх сил відносно центру ваги цього перерізу та позначається M_x або M.

Із рівноваги правої частини балки (рис. 62, в) можна зробити висновок, що поперечна сила Q_y та згинальний момент M_x в перерізі будуть мати ті ж самі значення, що і в лівій частині, але протилежні за напрямком.

Із рівнянь рівноваги ми визначили, що поперечна сила в довільному перерізі бруса чисельно дорівнює алгебраїчній сумі проекцій всіх зовнішніх сил, що діють по одну сторону від перерізу, на вісь, перпендикулярну до осі бруса.

Згинальний момент в довільному перерізі бруса чисельно дорівнює алгебраїчній сумі моментів всіх зовіншніх сил, що діють по одну сторону від перерізу, відносно його центру ваги.

Щоб отримати в одному і тому ж перерізі балки один і той же знак для поперечної сили або згинального моменту, незалежно від того, яку частину балки ми розглядаємо, прийняті наступні правила знаків:

а) поперечна сила в довільному перерізі буде додатною, якщо зовнішня сила, що діє на ліву відсічену частину, направлена знизу вверх, а на праву відсічену частину – зверху вниз (рис. 63, а). В протилежному випадку поперечна сила буде відємна (рис. 63, б).

б) згинальний момент в довільному перерізі балки буде додатним, якщо зовнішня сила, що діє на відсічену частину, згинає її відносно перерізу випуклістю вниз (рис. 64, а). В протилежному випадку згинальний момент буде відємним (рис. 64, б).

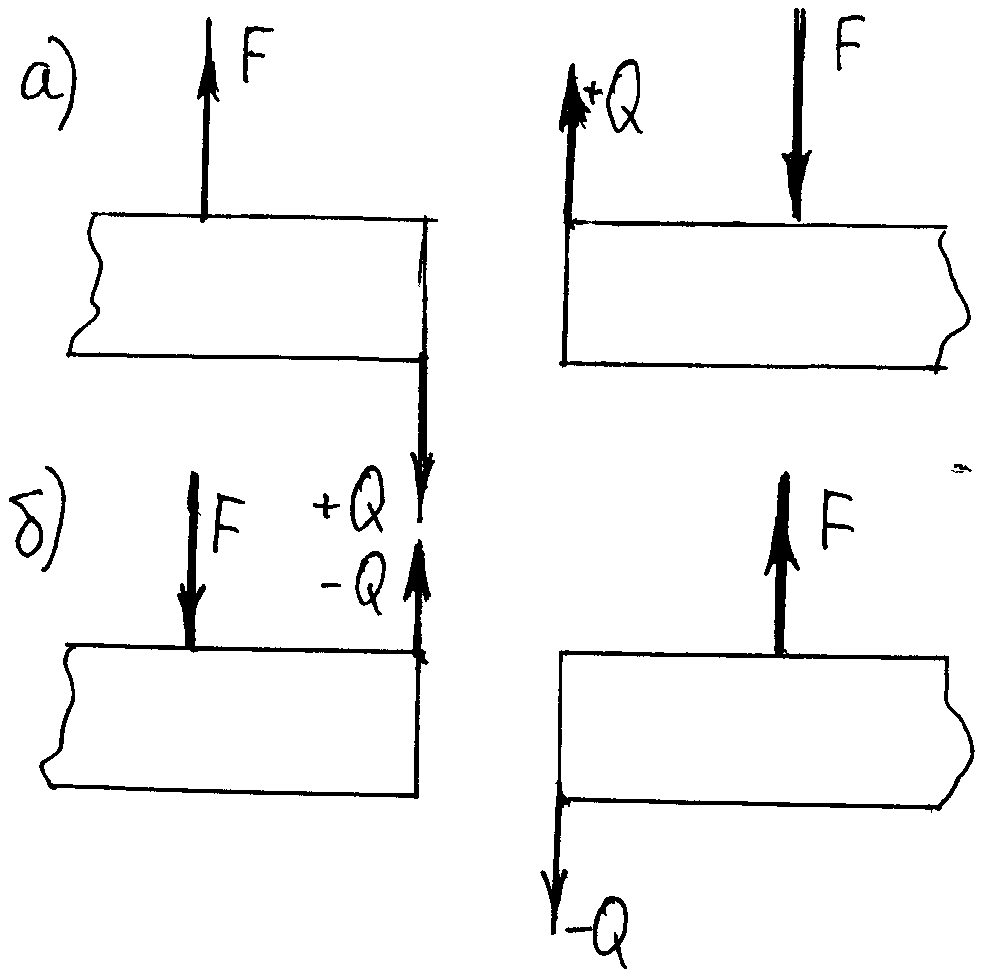
Рис. 63 Рис. 64