32.2. Распределения Ферми-Дирака и Бозе-Энштейна

Обозначим g_k — число возможных состояний частицы с энергией W_k. Например, если частица электрон в атоме водорода, то число таких состояний 2n², где n — главное квантовое число. Пусть далее n_k — число частиц с энергией W_k. Если эти частицы фермионы, то в соответствии с принципом Паули данное состояние может быть либо свободным (n_k=0), либо занятым (n_k=1), т.е. n_k принимает лишь два значения — 0 или 1. Для бозонов в данном состоянии может быть сколько угодно частиц, т.е. n_k может принимать любые целые значения 0, 1, 2, ... .

Основная задача квантовой статистики — найти функцию распределения частиц по энергии, т.е. такую функцию f_k, которая будучи умноженной на число возможных состояний с энергией W_k, давала бы среднее число частиц, обладающих данной энергией W_k:

.

(32.1)

Функция распределения f_k характеризует вероятность того, что данное энергетическое состояние занято.

Для фермионов эта функция имеет вид (см. прил. 8)

,

(32.2)

и называется функцией распределения Ферми-Дирака.

Энергия W_F называется энергией Ферми. Чтобы выяснить физический смысл энергии Ферми, рассмотрим поведение функции (32.2) вблизи абсолютного нуля, т.е. при . Если W_n<W_F, то при , и, следовательно, f_n=1. Если же W_n>W_F, то при , и, следовательно, f_n=0. Таким образом, при абсолютном нуле энергия Ферми имеет смысл предельной энергии: все состояния с энергией W_n<W_F заняты, а с энергией W_n>W_F вакантны.

Рис. 32.1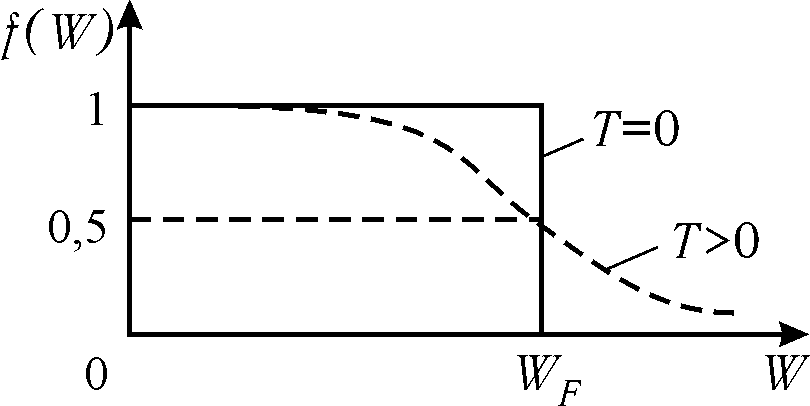

График функции распределения Ферми-Дирака при T=0 показан на рис. 32.1 сплошной линией. По мере возрастания температуры график функции распределения становится более пологим (пунктирная кривая); состояния с энергией порядка (kT), меньшей W_F, начинают частично освобождаться, а состояния с энергией порядка kT, но большей W_F, начинают частично «заселяться». Можно показать, что вероятность заполнения состояния с энергией Ферми при T ≠ 0 равна 0,5.

Для систем, состоящих из переменного числа бозонов (фотонов, фононов — см. §  33.2) функция распределения имеет вид (см. прил. 8)

,

(32.3)

и называется функцией распределения Бозе-Энштейна. С учетом того, что энергия фотона (фонона) W=h, распределение Бозе-Энштейна принимает вид

.

(32.4)

Лекція 45.

Фiзика твердого тiла

Елементи зонної теорiї кристалiв. Дiелектрики, метали, напiвпровiдники.

33. Физика твердого тела

33.1. Элементы зонной теории кристаллов

Рис. 33.1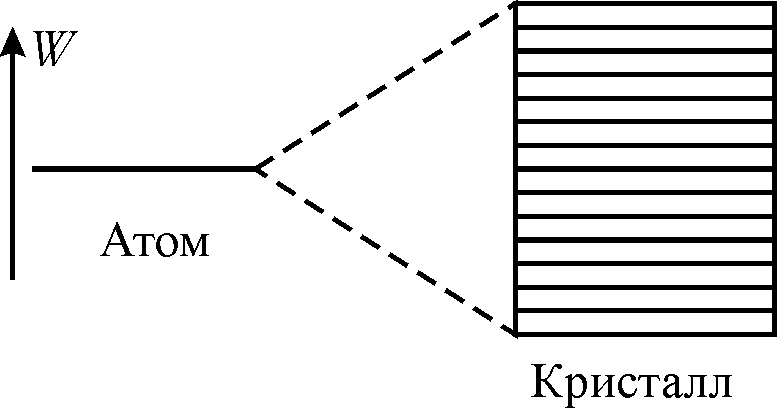

В прил. 7 показано, что при сближении атомов и образовании двухатомной молекулы энергетические уровни атомов расщепляются на два подуровня энергии. Аналогично можно показать, что при сближении N атомов и их объединении в единое целое (кристалл) вследствие взаимодействия атомов их энергетические уровни расщепляются на N близко отстоящих подуровней (рис. 33.1). Такую совокупность подуровней, возникшую в результате расщепления исходного энергетического уровня атомов, будем далее называть разрешенной зоной энергии (или просто разрешенной зоной). Расстояния между подуровнями энергии в пределах разрешенной зоны составляют ~10^‑23 эВ, что значительно меньше энергии теплового движения частиц (kT~10^-2 эВ).

Распределение электронов по энергетическим подуровням в пределах разрешенной зоны определяется принципом минимума энергии (согласно которому сначала заполняются подуровни с меньшими значениями энергии) и принципом Паули.

Рассмотрим, например, уровень энергии атома с главным квантовым числом n=1. Этот уровень невырожден, так как ему соответствует лишь одно значение орбитального квантового числа. При образовании кристалла этот уровень образует зону, состоящую из N подуровней. В такой зоне в соответствии с принципом Паули может разместиться не более, чем 2N электронов.

Рассмотрим теперь уровень энергии атома с n=2, l=1. Такой уровень энергии трехкратно вырожден, так как орбитальному квантовому числу l=1 соответствуют значения магнитного квантового числа: m=-1, 0, +1. В кристалле вырождение снимается: образуется 3N подуровней энергии. Следовательно, максимальное число электронов, которые могут разместиться в зоне, порожденной уровнями энергии атома с n=2, l=1, равно 23N = 6N. Аналогичным образом анализируют и другие зоны.

Зоны в кристалле могут быть не заполненными электронами, заполненными полностью или частично. Результат заполнения зависит от того, каким уровнем энергии атома порождена зона. Рассмотрим различные случаи.

Пусть на уровне энергии атома с квантовыми числами n=1, l=0 находятся два электрона с противоположными спинами. Если в кристалле имеется N атомов, то в соответствующей зоне будет N подуровней, на каждом из которых разместится по два электрона (всего 2N электронов). Таким образом, в данном случае получится полностью заполненная зона.

Если на уровне атома с n=2, l=0 (как, например, у атома лития) находится один электрон, то в кристалле из N атомов будет N электронов. Всего же подуровней в зоне — 2N. Поэтому такая зона будет заполнена наполовину.

Незаполненная (пустая) зона образуется в том случае, если на соответствующем уровне энергии атома нет ни одного электрона.

Электрические свойства твердых тел определяются взаимным расположением заполненных, частично заполненных и пустых зон. В зависимости от конкретной ситуации твердое тело обладает различными электрическими свойствами. На основе зонной теории все твердые тела по их электрическим свойствам можно разбить на три основные группы: металлы, диэлектрики и полупроводники.

Твердое тело можно отнести к одной из этих групп в зависимости от расположения валентной зоны и зоны проводимости. Валентной зоной (ВЗ) называется самая высокая из полностью заполненных электронами зон (рис. 33.2). Следующая зона после валентной называется зоной проводимости (ЗП). Зона проводимости может быть либо частично заполненной электронами, либо незаполненной (рис. 33.2,а,б).

Электрические свойства твердых тел определяются взаимным положением валентной зоны и зоны проводимости, а также тем, пуста ли зона проводимости или заполнена частично. В связи с этим нет необходимости рассматривать все зоны кристалла, достаточно рассмотреть указанные. Если зона проводимости частично заполнена электронами, то мы имеем дело с металлами (рис. 33.3). Рассмотрим случай, когда зона проводимости пуста. Электроны находятся в валентной зоне, которая отделена от зоны проводимости валентной зоной. В зависимости от ширины запретной зоны различают диэлектрики и полупроводники. Четкой границы в такой классификации нет. Принято считать, что твердое тело является диэлектриком, если ширина запретной зоны W > 4 эВ; если же W < 4 эВ, то такое тело относится к полупроводникам.

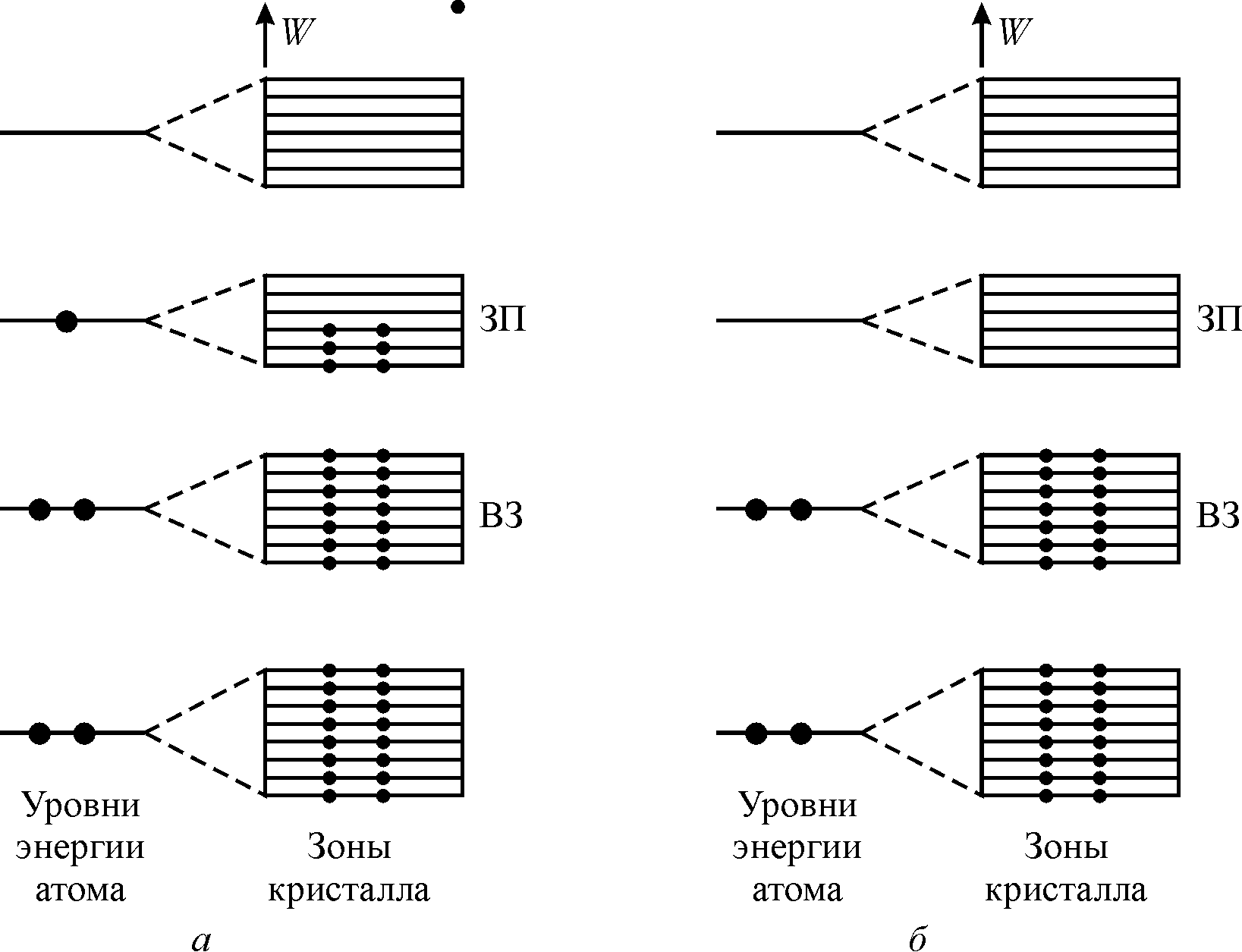
Рис. 33.2

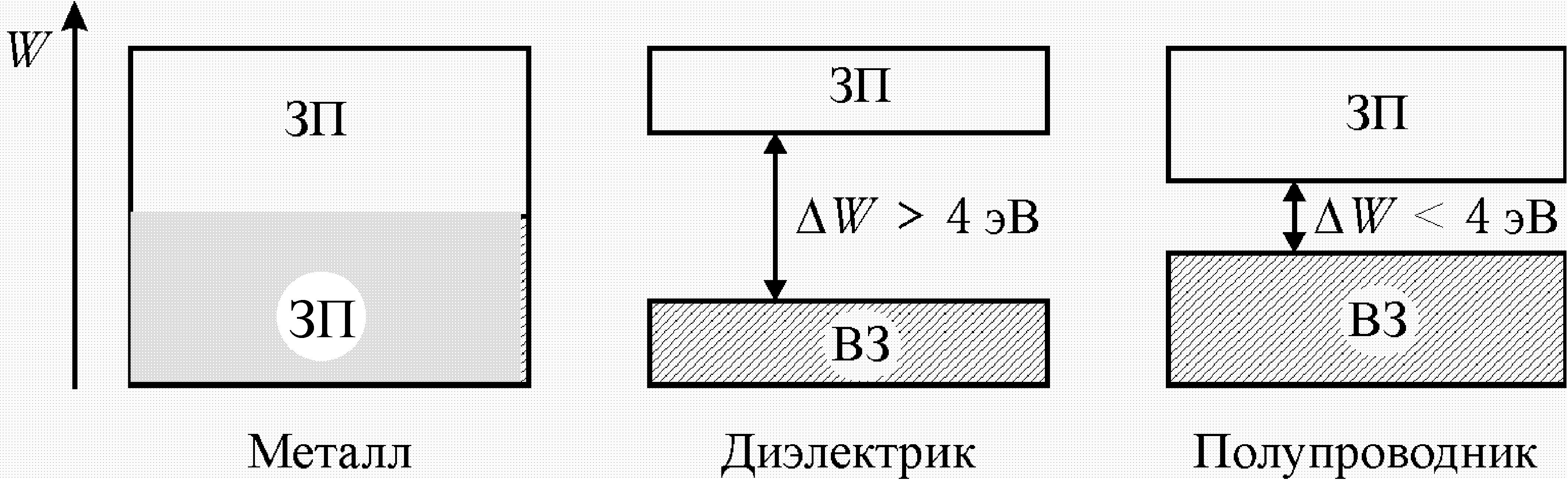
Рис. 33.3