31.2. Опыт Штерна и Герлаха. Спин электрона

Пространственное квантование момента импульса электрона в атоме было подтверждено в опытах Штерна и Герлаха (1922 г.).

Ранее (см. § 19.2) было показано, что с орбитальным моментом импульса связан орбитальный магнитный момент p_m. При пропускании пучка атомов через неоднородное магнитное поле на них будет действовать сила

.

(31.5)

где  — угол между вектором и направлением внешнего магнитного поля. В силу пространственного квантования момента импульса и магнитного момента этот угол может приобретать лишь ряд дискретных значений, поэтому пучок атомов, проходящих через неоднородное магнитное поле, будет расщепляться на 2l+1 пучков, где l — орбитальное квантовое число.

Рис. 31.2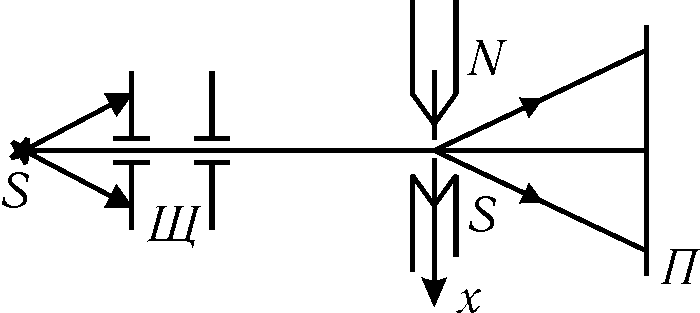

Схема опыта Штерна и Герлаха показана на рис. 31.2, где S — источник атомов; Щ — щели, формирующие атомный пучок: N, S — полюса магнита, создающие магнитное поле высокой неоднородности; n — экран, на котором фиксируется положение пролетевших атомов. В опытах Штерна и Герлаха наблюдалось расщепление атомных пучков, что подтверждало квантово-механический эффект пространственного квантования.

Наиболее интересные результата были получены в этом опыте при изучении пучка атомарного водорода. В основном состоянии у атомарного водорода n=0, l=0, т=0 и, следовательно, расщепления пучка атомов в магнитном поле не должно происходить. Однако в эксперименте наблюдалось раздвоение пучка. Для объяснения этого неожиданного результата было выдвинуто предположение о том, что электрон, кроме орбитального магнитного момента, характеризуется собственным механическим и, следовательно, магнитным моментом, названным спином.

Величина собственного механического момента электрона (в единицах h) определяется спиновым квантовым числом s. Число возможных ориентаций спинового момента электрона (так же как орбитального) должно определяться соотношением 2s+1, а поскольку было экспериментально установлено, что происходит расщепление на два пучка, то 2s+1 и s=1/2. В одном из пучков спин электрона ориентирован вдоль поля, а в другом — в противоположном направлении — этим состояниям сопоставляются значения спинового квантового числа s=+1/2 и s=–1/2.

Первоначально предполагалось, что спин обусловлен вращением электрона вокруг собственной оси. Однако такая механическая модель вызвала ряд затруднений и была оставлена. Спин — это внутреннее неотъемлемое свойство электрона, которое не имеет механической аналогии. Как в последствии показал П. Дирак, существование спинового момента электрона автоматически вытекает из соответствующего квантово-механического уравнения (уравнения Дирака), в котором учтены положения теории относительности.

31.3. Принцип Паули. Периодическая система элементов Менделеева

Состояние электрона в атоме определяется с помощью четырех квантовых чисел n, l, m, s. Физические величины, определяемые этими числами, и возможные их значения приведены в табл. 31.1.

Таблица 31.1

Квантовое число	Обозначение	Возможные значения	Физическая величина
Главное	n	1, 2, 3, ...	Энергия
Орбитальное	l	0, 1, ..., (n-1)	Момент импульса
Магнитное	m	-l, -(l-1), ..., 0, ..., +l	Проекция момента импульса на выделенное направление
Спиновое	s	+1/2, -1/2	Проекция собственного механического момента (спина) на выделенное направление

В 1925 г. В._Паули установил принцип: в любом атоме не может быть двух электронов с одинаковым набором квантовых чисел, т.е. электроны должны отличаться друг от друга хотя бы одним квантовым числом.

Пользуясь принципом Паули, можно найти максимальное число электронов с одинаковым значением главного квантового числа и отличающихся друг от друга хотя бы одним квантовым числом l, m, s. Различные состояния атома, характеризующиеся значением главного квантового числа n=1 и n=2, приведены в табл. 31.2. Видно, что максимальное число электронов, находящихся в состоянии с n=1, равно двум, а при n=2 это число равно восьми. В общем случае максимальное число электронов, которые находятся в состоянии со значением главного квантового числа n, равно 2n².

Электроны с одинаковым значением главного квантового числа образуют оболочки, которые обозначаются буквами K (n=1), L (n=2), M (n=3) и т.д. В каждой из оболочек электроны распределяются по подоболочкам, соответствующим значению орбитального квантового числа l. Число подоболочек равно порядковому номеру n оболочки. Максимальное число электронов в подоболочке с данным l равно 2(2l+1). В порядке возрастания орбитального квантового числа l=0, 1, 2, 3, 4, ... подоболочки обозначаются буквами соответственно s, p, d, e, f.

Таблица 31.2

Главное квантовое число		Орбитальное квантовое число	Магнитное квантовое число	Спиновое квантовое число	Максимальное число электронов
1	K-оболочка	0	0	+1/2	2
1		0	0	-1/2
2		0	0	+1/2
2		0	0	-1/2	s-подоболочка
2		0	-1	+1/2
2	L-оболочка	0	-1	-1/2
2		1	0	+1/2	8
2		1	0	-1/2	p-подоболочка
2		1	1	+1/2
2		1	1	-1/2

Теоретическое обоснование периодической системы элементов Менделеева основано на трех положениях.

1. Общее число электронов в атоме данного элемента равно его порядковому номеру в таблице Менделеева. Это означает, что суммарный отрицательный заряд электронов компенсирует положительный заряд ядра и поэтому атом в целом электронейтрален.

2. При заполнении электронных оболочек должен выполняться принцип минимума энергии, который состоит в том, что при переходе от одного элемента к другому, т.е. при присоединении к атому нового электрона, в первую очередь заполняются состояния с наименьшей энергией.

3. Заполнение электронами энергетических состояний в атоме происходит в соответствии с принципом Паули.

Исходя из этих принципов, рассмотрим теперь строение начальных периодов таблицы Менделеева.

Первый период содержит два элемента — водород и гелий. В атоме водорода имеется один электрон, который заполняет состояние с квантовыми числами n=1, l=0, m=0, s=+1/2 или –1/2. В атоме гелия два электрона имеют одинаковые числа n=1, l=0, m=0, но разные значения спиновых квантовых чисел: для одного из них s=+1/2, а для другого s=–1/2. Эти два электрона полностью заполняют наинизшую K-оболочку.

Второй период начинается с атома лития, который имеет три электрона: два из них образуют K-оболочку, а третий находится на L-оболочке, соответствующей значению главного квантового числа n=2. Следующие далее по мере возрастания номеров элементы Be, B, C, N, O, F, Ne также имеют полностью заполненную K-оболочку, а остальные электроны заполняют L-обо­лочку, причем сначала заполняется подоболочка s (Li, Be), а затем подоболочка p — остальные элементы второго периода. Заполнение p-оболочки заканчивается на атоме неона и им же завершается второй период периодической системы.

C третьего периода, т.е. со щелочного элемента натрия, начинается заполнение M-оболочки (n=3): сначала заполняется s-подоболочка (Na, Mg), а затем p-подоболочка. Заканчивается период инертным газом аргоном, у которого p-подоболочка полностью заполнена.

В соответствии с принципом минимума энергии оболочки должны быть последовательно заполнены одна за другой, а в пределах каждой оболочки - сначала s-подоболочка, затем p-, d-, f-подоболочки. Однако, начиная с четвертого периода такой порядок нарушается: сначала заполняется более высокая подоболочка, а затем более низкая. Как показывают строгие квантово-механические расчеты, это связано с тем, что энергия электрона зависит не только от главного квантового числа, но и от орбитального. Поэтому энергетически более выгодным может оказаться состояние с большим n, но меньшим l.

Группу элементов от лантана (La₅₇) до лютеция (Lu₇₁) называют лантаноидами или редкоземельными элементами. У них происходит заполнение внутренних оболочек при практически неизменных внешних оболочках, поэтому лантаноиды характеризуются близкими химическими свойствами, подобным образом ведут себя актиноиды — группа элементов от актиния (Ac₈₉) до лоуренсия (Lr₁₀₃) в седьмом периоде.

Лекція 43.

Рентгенiвськi спектри. Молекулярнi спектри. Комбiнацiйне розсiювання свiтла. Люмiнесценцiя.