3. Случайные величины
3.1. Основные понятия
В исследуемых социально – экономических системах нас часто интересуют такие величины, которые от наблюдениях к наблюдению принимают разные числовые значения. Например, у каждого человека имеется много числовых характеристик: рост, возраст, вес и т. д. Если мы выбираем человека случайно (например, из группы или из толпы), то случайными будут и значения указанных характеристик.
Случайной называется величина, которая в результате испытания принимает одно возможное значение, заранее не известное и зависящее от случайных причин. Случайные величины обозначаются заглавными буквами X, Y, Z,… латинского алфавита, а их возможные значения — соответствующими строчными буквами x, у, z,… В практических задачах обычно используются два вида случайных величин - дискретные и непрерывные.
Дискретной называется случайная величина (СВ), которая может принимать конечное или счетное множество значений (счетным называют множество, элементы которого можно пронумеровать).
Например. 1) Число родившихся детей в течение суток в Нижнем Новгороде.
2) Число очков, выпадающее при бросании игральной кости.
3) Выбирая наугад слова из текста, мы встречаем слова разной длины, с различным количеством гласных или согласных фонем.
Непрерывной называют случайную величину, бесконечное множество значений которой есть некоторый интервал (конечный или бесконечный) числовой оси.
Например. 1) Расход электроэнергии на предприятии за месяц.
2) Интенсивность звука, которая колеблется обычно в определённых пределах.
Законом распределения случайной величины X называется определённое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями.
Например. 1) Вероятность появления букв, цифр и символов в принимаемом сообщении.
2) Ежедневная прибыль фирмы, рассчитанная по многолетним статистическим данным
3.2. Способы задания закона распределения дискретной св
Табличный. Простейшей формой задания закона распределения дискретной СВ является таблица (матрица),
X |
x1 |
x2 |
… |
xi |
… |
xn |
|
p |
p1 |
p2 |
… |
pi |
… |
pn |
|
Графический. Ряд распределения может быть изображен графически, если по оси абсцисс откладывать значения случайной величины, по оси ординат – соответствующие им вероятности. Соединение полученных точек образует ломаную линию, называемую многоугольником распределения вероятностей.
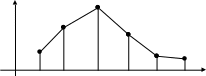p
x1 x2 xi xn x
Аналитический (в виде формулы). Закон распределения может быть задан или функцией распределения или плотностью распределения. Например, формула Бернулли описывает Биномиальный закон через плотность распределения. Для описания закона распределения случайной величины можно рассматривать вероятности события X<x, где x – текущая переменная, т. е. некоторую функцию от x.
Функцией распределения случайной величины X называется функция F(x), выражающая для каждого x вероятность того, что случайная величина X примет значения, меньшее x.
F(x)=P(X<x),
или
.
Функцию F(x) называют также интегральной функцией распределения или интегральным законом распределения.