5.6. Построение доверительного интервала для оценки дисперсии по выборке из нормальной генеральной совокупности

Доверительный интервал для оценки неизвестной дисперсии вычисленной по выборке объёма n

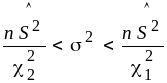
определяется законом распределения Пирсона ( - распределение) с n или n-1 степенями свободы в зависимости от рассматриваемого случая: известно или неизвестно априори МО M(X), а также исправленной выборочной дисперсией . С учётом несимметричности распределения Пирсона, для расчета значений и зададим вероятности , и , где . По таблицам распределения (приложение 3) определим соответствующие значения двух пороговых уровней , , и подставим эти найденные значения в выражение для доверительного интервала.

Таким образом, с доверительной вероятностью значение неизвестной дисперсии не выходит за пределы доверительного интервала

.

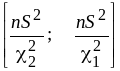Его длина стремится к нулю при .

Пример 39 Найти доверительный интервал для оценки неизвестной дисперсии, соответствующий доверительной вероятности р=0,8 в условиях примера 38.

Решение. Для доверительной вероятности р=0,8 значение и . По таблице распределения Пирсона (приложение 3) для числа степеней свободы n-1=19 и находим =27,2, а для получаем =11,65. С учётом ранее вычисленного значения находим доверительный интервал для дисперсии

=[0,045; 0,104].

Вопросы и задачи

1. Что характеризуют среднее значение и разброс выборки (дисперсия наблюдений) ?

2. Найти и по выборке

   0.3, 0.33, 0.37, 0.36, 0.31, 0.29, 0.34, 0.39, 0.37, 0.38, 0.35, 0.32, 0.39, 0.3, 0.32, 0.32, 0.38, 0.37, 0.38, 0.33, 0.37, 0.33, 0.34, 0.33, 0.3, 0.34, 0.36, 0.33, 0.34, 0.36, 0.29, 0.3, 0.33, 0.32, 0.32, 0.38, 0.37, 0.34, 0.35, 0.36

3. Каким критериям должна удовлетворять статистическая оценка?

4. Найти по методу максимального правдоподобия точечную оценку неизвестных параметра m и  нормального распределения.

5. В условиях примера 38 найти доверительный интервал, если дисперсия известна и равна 0,064. Сравнить результат с ранее полученным.

6. Независимая выборка наблюдений объемом n =40:

0.3, 0.33, 0.37, 0.36, 0.31, 0.29, 0.34, 0.39, 0.37, 0.38, 0.35, 0.32, 0.39, 0.3, 0.32, 0.32, 0.38, 0.37, 0.38, 0.33, 0.37, 0.33, 0.34, 0.33, 0.3, 0.34, 0.36, 0.33, 0.34, 0.36, 0.29, 0.3, 0.33, 0.32, 0.32, 0.38, 0.37, 0.34, 0.35, 0.36

взята из нормального распределения с неизвестными параметрами. Найти доверительный интервал для оценки математического ожидания при доверительной вероятности р=0,8. (0.332 0.351)

7. Найти доверительный интервал в условиях примера 39 для доверительной вероятности р=0,9. Сравнить с ранее полученным результатом.

6. Проверка статистических гипотез

Статистическая гипотеза - любое высказывание или суждение о статистических свойствах или законе распределения анализируемой СВ. Основной является задача проверки нулевой гипотезы против альтернативы на основании имеющихся выборочных данных конечного объёма .