Свойства функции распределения

1. Функция распределения F(x, y) есть неотрицательная функция, заключенная между нулем и единицей

.

2. Функция распределения F(x, y) есть неубывающая функция по каждому из аргументов, т. е.

3. Если хотя бы один из аргументов обращается в , то функция распределения F(x, y) равна нулю, т. е.

4. Если один из аргументов обращается в 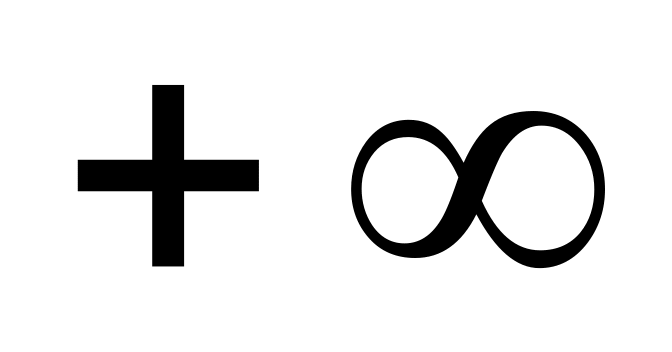, то функция распределения F(x, y) становится равной функции распределения случайной величины, соответствующей другому аргументу:

,

.

5. Если оба аргумента равны 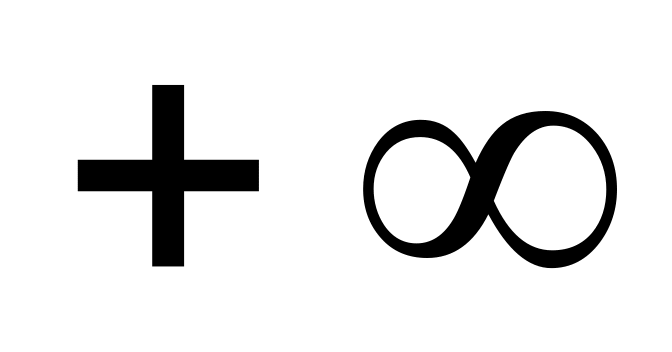, то функция распределения равна единице:

6. Зная функцию распределения F(x, y), можно найти вероятность попадания случайной точки (X,Y) в пределы прямоугольника ABCD

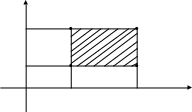
y₂ A(x_1, y₂) B(x₂, y₂)

y₁

D(x₁, y₁) C(x₂, y₁)

0 x₁ x₂

.

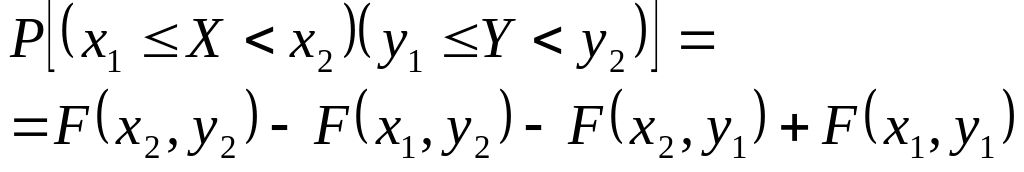Пример 30. Задана функция распределения двумерной случайной величины

.

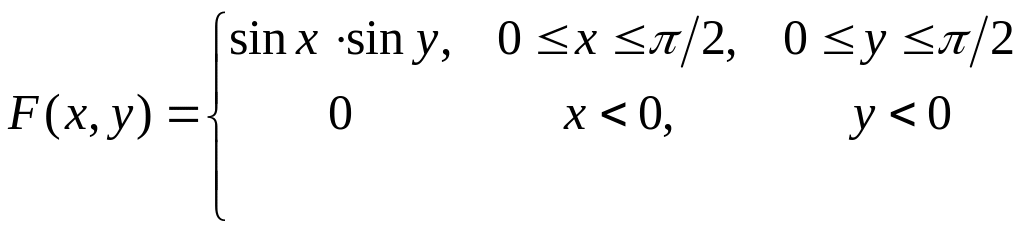Найти вероятность попадания случайной точки (X, Y) в прямоугольник, ограниченный прямыми

Решение. Используя свойство 6, положим , , , , найдем

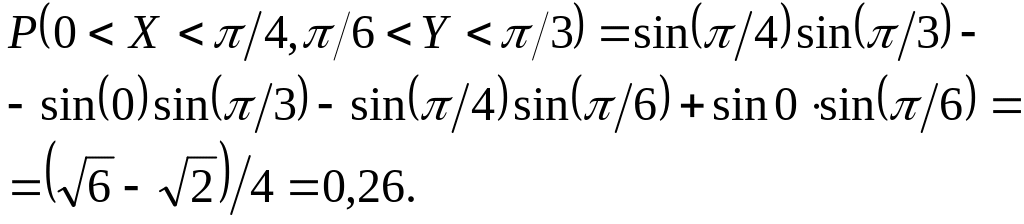
4.3 Двумерные непрерывные случайные величины

Двумерная случайная величина (X, Y) называется непрерывной, если её функция распределения F(x,y) – непрерывная функция, дифференцируемая по каждому из аргументов, и существует вторая смешанная производная .

Плотностью вероятности (плотностью распределения или совместной плотностью) непрерывной двумерной случайной величины (X, Y) называется вторая смешанная частная производная её функции распределения, т. е.

.

Геометрически плотность вероятности двумерной непрерывной случайной величины (X,Y) представляет собой поверхность распределения f(x, y), в пространстве Oxyz.

Свойства плотности вероятности f(X, y)

1. Плотность вероятности f(x, y) есть неотрицательная функция, т. е.

.

2. Вероятность попадания непрерывной двумерной величины (X, Y) в область D равна

Поясним геометрически эту формулу.

Введем понятие «элемент вероятности» для двумерной непрерывной случайной величины (X, Y), равный f(x, y)dxdy. Он представляет вероятность попадания случайной точки (X, Y) в элементарный прямоугольник со сторонами dx и dy .

y

y+dy

y

0 x x+dx x

Эта вероятность приближенно равна объему элементарного параллелепипеда с высотой f(x, y), опирающегося на элементарный прямоугольник со сторонами dx и dy. Итак, вероятность попадания непрерывной двумерной величины (X, Y) в область D на плоскости Oxy геометрически изображается объёмом цилиндрического тела, ограниченного сверху поверхностью распределения f(x, y) и опирающегося на область D, а аналитически – двойным интегралом.

3. Функция распределения непрерывной двумерной случайной величины может быть выражена через её плотность вероятности f(x, y) по формуле

4. Двойной несобственный интеграл в бесконечных пределах от плотности вероятности двумерной случайной величины равен единице:

.

В этой формуле несобственный интеграл есть вероятность попадания во всю плоскость Oxy, т. е. вероятность достоверного события, равная единице. Это означает, что полный объём тела, ограниченного поверхностью распределения и плоскостью Oxy, равен 1.

Пример 31. Задана функция распределения двумерной случайной величины

.

Найти двумерную плотность вероятности системы.

Решение. Используем формулу

.

Найдем частные производные:

,

.

Итак, искомая двумерная плотность вероятности

.