
- •Математический анализ
- •1.Пределы
- •2.Элементы дифференциального исчисления
- •1. Производная
- •2. Дифференциал
- •3. Производные высших порядков
- •4. Исследование функций
- •3.Элементы интегрального исчисления
- •1. Неопределенный интеграл
- •2. Определенный интеграл
- •4.Функции нескольких переменных
- •1. Частные производные
- •2. Кратные интегралы
- •6.Дифференциальные уравнения
- •1. Уравнения с разделяющимися переменными
- •2. Однородные уравнения
2. Кратные интегралы
П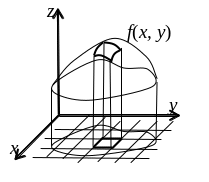 усть
имеется некоторая поверхность, задаваемая
в трехмерном пространстве функцией z
= f(x,
y). На плоскости xOy
выделена некоторая фигура G,
в точках которой f(x,
y)
0. Через каждую точку ее границы проведена
вертикальная прямая, называемая
образующей; эти прямые вместе
образуют цилиндрическую поверхность.
(Обычная круговая цилиндрическая
поверхность образуется таким же образом:
образующие проходят через границу
круга). Требуется определить объем
тела, ограниченного этой цилиндрической
поверхностью, плоскостью xOy
и поверхностью z =
f(x,
y).
усть
имеется некоторая поверхность, задаваемая
в трехмерном пространстве функцией z
= f(x,
y). На плоскости xOy
выделена некоторая фигура G,
в точках которой f(x,
y)
0. Через каждую точку ее границы проведена
вертикальная прямая, называемая
образующей; эти прямые вместе
образуют цилиндрическую поверхность.
(Обычная круговая цилиндрическая
поверхность образуется таким же образом:
образующие проходят через границу
круга). Требуется определить объем
тела, ограниченного этой цилиндрической
поверхностью, плоскостью xOy
и поверхностью z =
f(x,
y).
Для решения этой задачи покроем плоскость xOy сеткой квадратов площадью ∆. В каждом квадрате, попавшем в область G, выберем точку (xi, yi), где i – номер квадрата. Построим прямоугольный параллелепипед, основанием которого является этот квадрат, а высота равна f(xi, yi). Эти параллелепипеды в совокупности образуют тело, близкое к измеряемому. Сумма их объемов приближенно равна искомому объему, причем чем меньше ∆, тем точнее это приближение. В пределе при ∆→ 0 получаем точное значение искомого объема. (На самом деле приведенные рассуждения годятся для достаточно простого случая, а в общем случае построение более тонкое).
Если в область G попало n квадратов и их стороны равны ∆x и ∆y, то ∆ = ∆x∆y, и сумма объемов параллелепипедов вычисляется по формуле
![]() =
=![]() .
.
Предел этой суммы называется двойным интегралом по области G от функции f(x, y) и обозначается
![]()
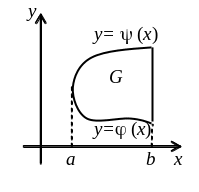 .
.
Для вычисления двойного интеграла его сводят к вычислению простых интегралов. Сначала выбирают порядок интегрирования. Пусть область G на плоскости xOy ограничена слева и справа прямыми x = a, x = b, а снизу и сверху графиками y = (x), y = (x) соответственно. Тогда двойной интеграл приводим к виду
=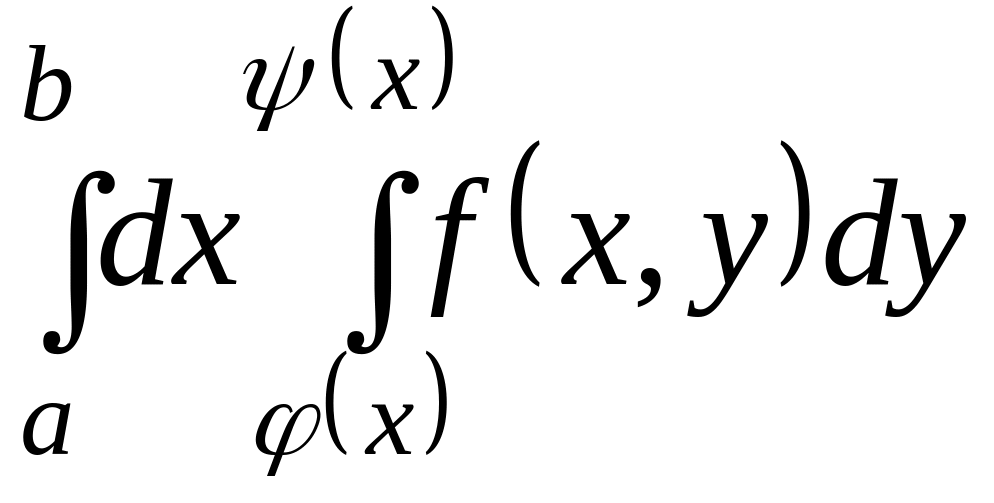 .
.
При этом при вычислении внутреннего интеграла по переменной y переменную x рассматриваем как константу.
П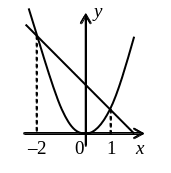 ример
1.4.3. Вычислить интеграл
ример
1.4.3. Вычислить интеграл
![]() по области D, ограниченной
линиями y = x2
и y = x
– 2.
по области D, ограниченной
линиями y = x2
и y = x
– 2.
Решение. Изобразим область D на рисунке. Точки пересечения линий найдем, решив уравнение x2 = x – 2. Получаем x = –2 и x = 1. Это будут пределы интегрирования для внешнего интеграла. Получаем
=![]() =
=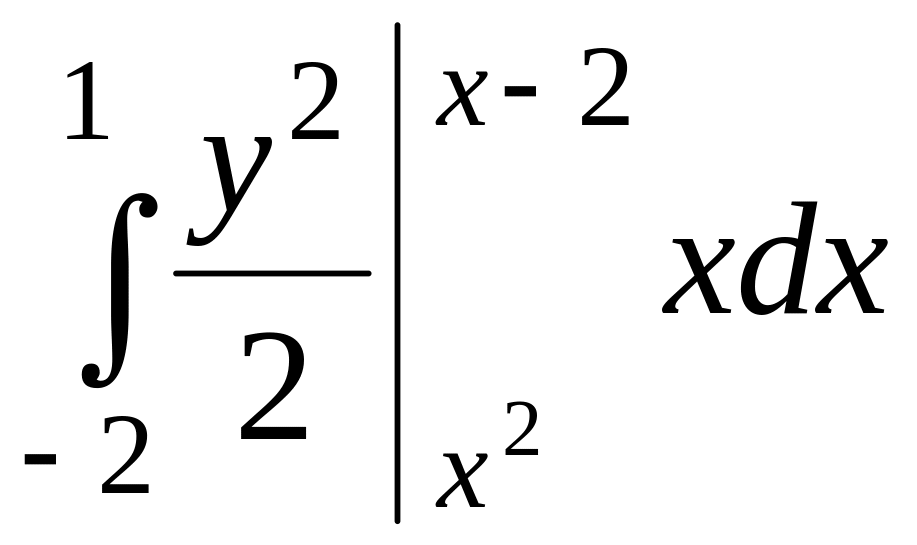 =
=![]() =
=
=
=![]() =
=![]() =
=![]() =
=
=
=![]() =
=![]() .
.
Аналогично двойному можно рассматривать тройной интеграл по пространственной области. С его помощью можно находить массу тела неоднородной плотности, силу притяжения двух близко расположенных тел и другие задачи.
У п р а ж н е н и я
1.4.1. Найдите частные производные первого и второго порядка по всем переменным для следующих функций:
z = x2y – ln xy;
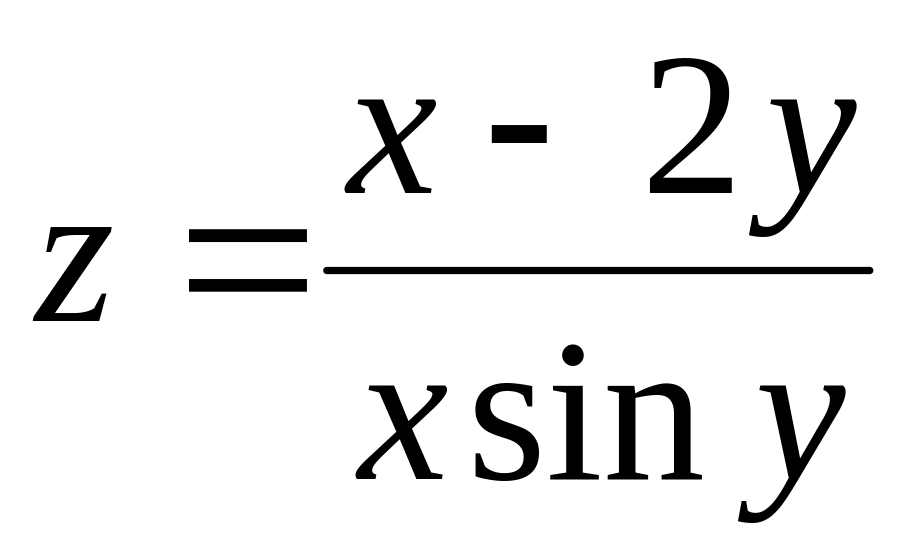 ;
;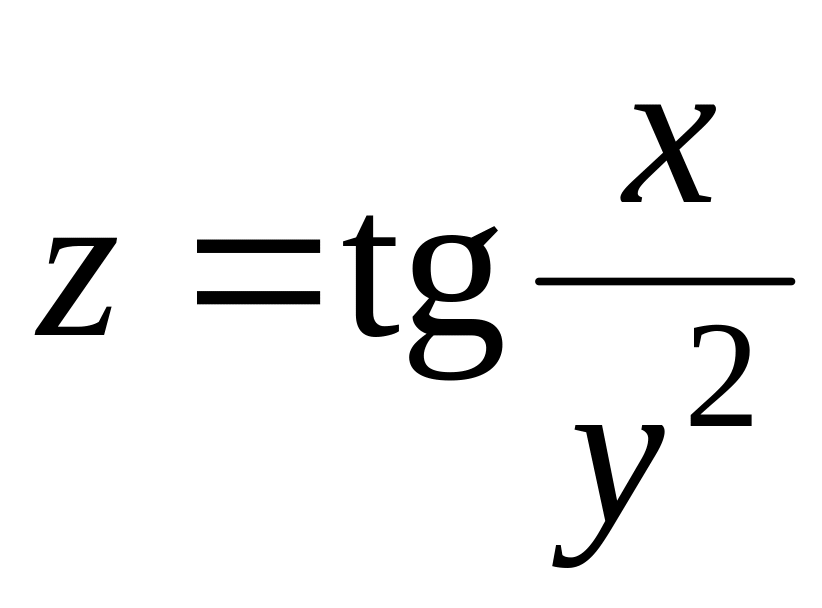 ;
;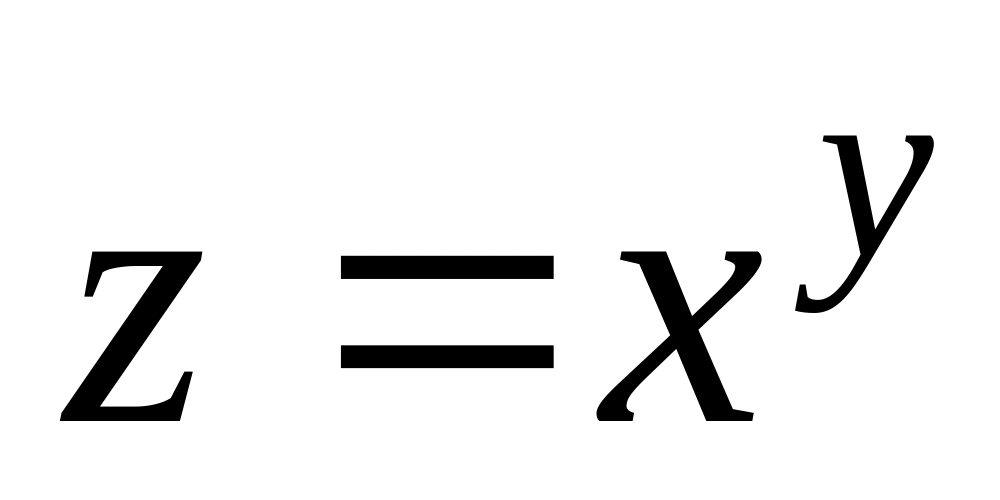 ;
;
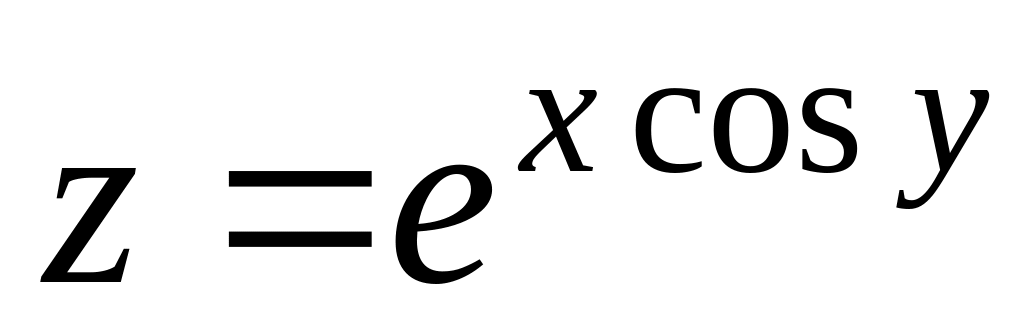 ;
;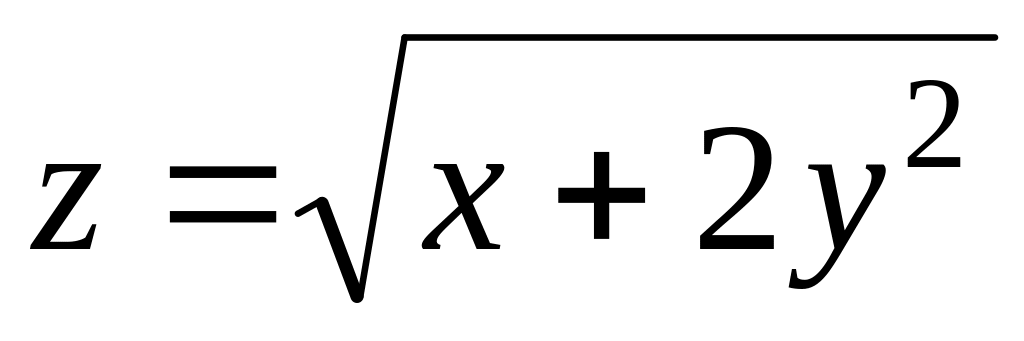 .
.
1.4.2. Вычислите двойной интеграл по области D, ограниченной указанными линиями:
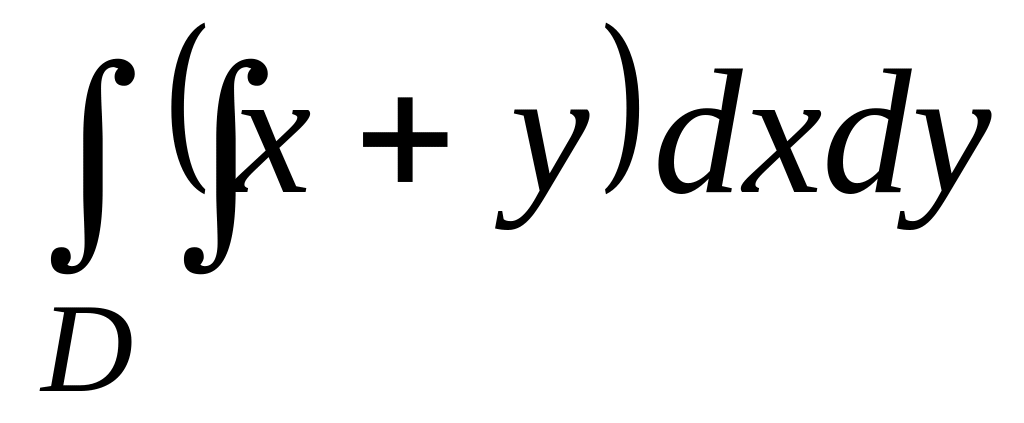 ,
x = 1, x
= 3, y =
0, y =
4;
,
x = 1, x
= 3, y =
0, y =
4;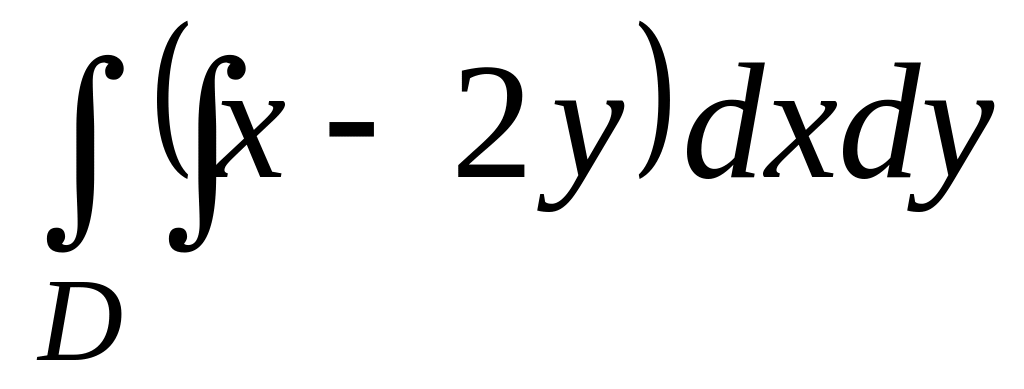 ,
y = x, y = 2
– x, x
= 3;
,
y = x, y = 2
– x, x
= 3;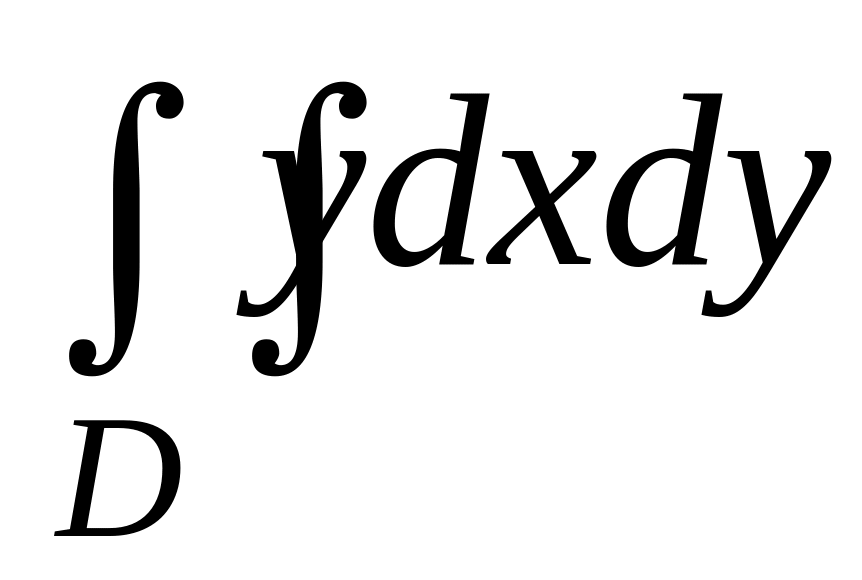 ,
y = x, y = 4
– x, y = 0;
,
y = x, y = 4
– x, y = 0;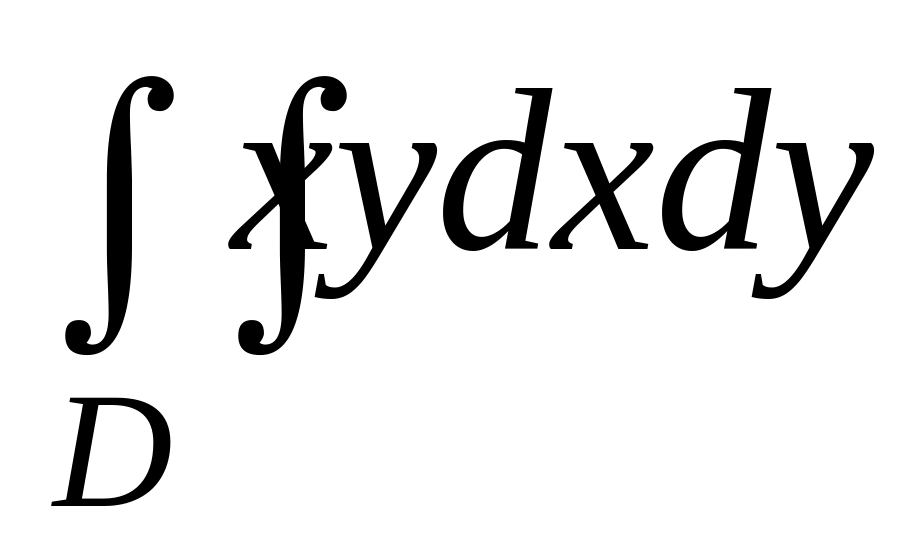 ,
y = x2
– 1, y = 1
– x2.
,
y = x2
– 1, y = 1
– x2.
5.Ряды
Числовым рядом называется бесконечная сумма чисел вида
a1 + a2
+ … + an
+ … =![]() .
.
Слагаемые этой суммы называются членами ряда.
Эту сумму, конечно, невозможно подсчитать непосредственно ввиду бесконечности числа слагаемых.
