
- •Для элементов линейного пространства операции сложения и умножения на действительное число обладают свойством …
- •В теории потребления предполагается, что функция полезности потребителя не обладает свойством …
- •Уравнение является …
- •Количество точек разрыва функции равно …
- •В теории потребления предполагается, что функция полезности потребителя обладает свойством …
- •7) Общее решение дифференциального уравнения имеет вид …
- •11) Максимальное значение целевой функции при ограничениях равно …
- •16) Уравнение является …
- •26) Уравнение является …
- •38) Уравнение является …
- •39) Производная второго порядка функции равна …
- •50) Производная второго порядка функции равна …
- •85) Производная второго порядка функции равна …
- •97) Производная второго порядка функции равна …
- •101) Область сходимости степенного ряда имеет вид …
- •Производная второго порядка функции равна …
- •Количество точек разрыва функции равно …
- •4) Уравнение является …
- •16) Общее решение дифференциального уравнения имеет вид …
- •30) Количество точек разрыва функции равно …
- •38) Область сходимости степенного ряда имеет вид …
- •40) В теории потребления предполагается, что функция полезности потребителя обладает свойством …
- •42) Неоклассическая производственная функция вида обладает свойством …
- •46) Производная второго порядка функции равна …
- •102)В теории потребления предполагается, что функция полезности потребителя обладает свойством …
- •Дискретная случайная величина X задана функцией распределения вероятностей Тогда вероятность равна …
- •В теории потребления предполагается, что функция полезности потребителя не обладает свойством
- •Уравнение является …
- •Общее решение дифференциального уравнения имеет вид …
- •Уравнение является …
- •Общее решение дифференциального уравнения имеет вид …
- •Максимальное значение целевой функции при ограничениях равно …
- •5.Производная второго порядка функции равна …
- •73.Частная производная второго порядка функции имеет вид …
- •85.Производная второго порядка функции равна …
- •Общее решение дифференциального уравнения имеет вид
- •Уравнение является
- •Дифференциальное уравнение будет однородным дифференциальным уравнением первого порядка при равном
- •Общее решение дифференциального уравнения имеет вид …
- •Матричная игра задана платежной матрицей Тогда соответствующая ей задача линейного программирования может иметь вид …
В теории потребления предполагается, что функция полезности потребителя не обладает свойством …
ОТВЕТ:
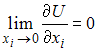
Функция
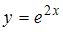 является
решением дифференциального уравнения
второго порядка …
является
решением дифференциального уравнения
второго порядка …
ОТВЕТ:
![]()
Решение задачи Коши
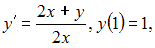 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Дифференциальное уравнение
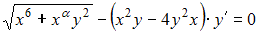 будет
однородным дифференциальным уравнением
первого порядка
при
будет
однородным дифференциальным уравнением
первого порядка
при 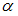 ,
равном …
,
равном …
ОТВЕТ: 4
Уравнение является …
ОТВЕТ: уравнением Бернулли
Значение производной второго порядка функции
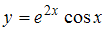 при
при 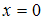 равно …
равно …
ОТВЕТ: 3
Множество первообразных функции
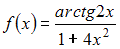 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Область определения функции
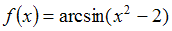 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Для определенного интеграла
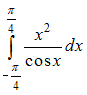 справедливо
равенство …
справедливо
равенство …
ОТВЕТ:
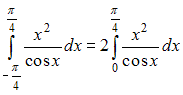
Количество точек разрыва функции равно …
ОТВЕТ: 1
Частная производная
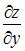 функции
функции 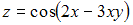 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Уравнение прямой, проходящей через точку пересечения прямых
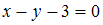 и
и 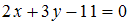 перпендикулярно
прямой
перпендикулярно
прямой 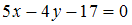 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
В полярной системе координат даны две точки
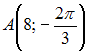 и
и 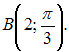 Тогда
полярные координаты середины отрезка
AB равны …
Тогда
полярные координаты середины отрезка
AB равны …
ОТВЕТ:
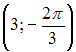
Уравнение плоскости, проходящей через точку
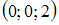 перпендикулярно
плоскостям
перпендикулярно
плоскостям 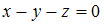 и
и 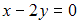 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Точки
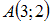 и
и 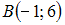 являются
концами одного из диаметров окружности.
Тогда уравнение окружности имеет вид …
являются
концами одного из диаметров окружности.
Тогда уравнение окружности имеет вид …
ОТВЕТ:
![]()
Частная производная
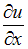 функции
функции 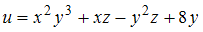 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Область определения функции
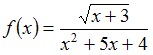 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Сумма числового ряда
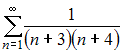 равна …
равна …
ОТВЕТ:
![]()
Если
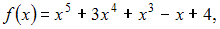 то
коэффициент a4 разложения
данной функции в ряд Тейлора по
степеням
то
коэффициент a4 разложения
данной функции в ряд Тейлора по
степеням 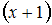 равен …
равен …
ОТВЕТ: -2
Радиус сходимости степенного ряда
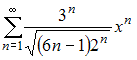 равен …
равен …
ОТВЕТ:
![]()
Эксцентриситет эллипса
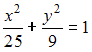 равен …
равен …
ОТВЕТ: 0,8
Уравнение геометрического места точек, равноудаленных от двух данных точек
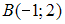 и
и 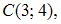 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Точка
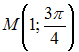 задана
в полярной системе координат, тогда ее
прямоугольные координаты равны …
задана
в полярной системе координат, тогда ее
прямоугольные координаты равны …
ОТВЕТ:
![]()
![]()
Даны три пары плоскостей: 1)
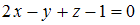 и
и 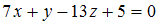 2)
2) 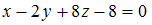 и
и 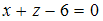 3)
3) 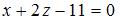 и
и 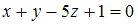 Тогда
…
Тогда
…
ОТВЕТ: перпендикулярна первая пара плоскостей
Мода вариационного ряда 2, 4, 5, 7, 7, 7, 9, 9, 11, 12 равна …
ОТВЕТ: 7
Правосторонняя критическая область может определяться из соотношения …
ОТВЕТ:
![]()
Выборочное уравнение прямой линии регрессии X на Y имеет вид
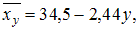 а
выборочные средние квадратические
отклонения равны:
а
выборочные средние квадратические
отклонения равны: 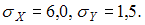 Тогда
выборочный коэффициент корреляции
Тогда
выборочный коэффициент корреляции 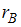 равен …
равен …
ОТВЕТ: –0,61
Дан доверительный интервал (20,2; 25,4) для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при увеличении объема выборки в четыре раза этот доверительный интервал примет вид …
ОТВЕТ: (21,5; 24,1)
Отрицательно определенная квадратичная форма может иметь вид …
ОТВЕТ:
![]()
Корень уравнения
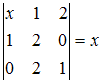 равен …
равен …
ОТВЕТ: – 3
Среди представленных множеств линейное пространство не образует …
ОТВЕТ:
множество
всех матриц размерностью ![]() содержащих
только положительные числа
содержащих
только положительные числа
Даны матрицы
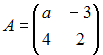 и
и 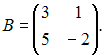 Если
матрица
Если
матрица 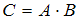 вырожденная,
то значение a равно …
вырожденная,
то значение a равно …
ОТВЕТ: – 6
Дана задача линейного программирования:
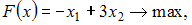 при
ограничениях:
при
ограничениях:
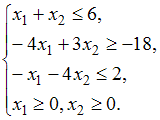 Тогда
канонический вид данной задачи будет
иметь вид …
Тогда
канонический вид данной задачи будет
иметь вид …
ОТВЕТ:
![]()

В матричной игре нижняя цена игры равна 3 для платежной матрицы …
ОТВЕТ:
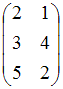
В транспортной задаче, решаемой методом потенциалов, распределение поставок задано таблицей:
 Тогда
значение потенциала v2 будет
равно …
Тогда
значение потенциала v2 будет
равно …
ОТВЕТ: – 2
Для сетевого графика, изображенного на рисунке,
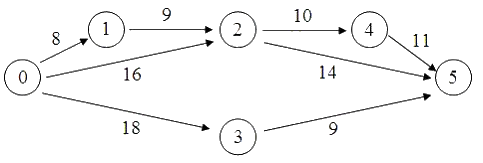 критический
путь имеет вид …
критический
путь имеет вид …
ОТВЕТ:
![]()
Для оценки с надежностью
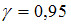 математического
ожидания
математического
ожидания 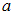 нормально
распределенного признака
нормально
распределенного признака 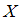 по
выборочной средней
по
выборочной средней 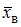 при
среднем квадратичном отклонении
при
среднем квадратичном отклонении 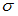 генеральной
совокупности использовали доверительный
интервал
генеральной
совокупности использовали доверительный
интервал 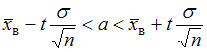 ,
где
,
где 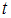 –
значение аргумента функции Лапласа
–
значение аргумента функции Лапласа 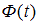 ,
при котором
,
при котором 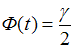 ,
, 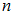 –
объем выборки.
Установите
соответствие между доверительными
интервалами и соответствующими
значениями
:
1)
–
объем выборки.
Установите
соответствие между доверительными
интервалами и соответствующими
значениями
:
1) 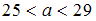 ,
2)
,
2) 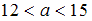 .
.
ОТВЕТ: 1 – 27
2 – 13,5
Для оценки с некоторой надежностью
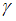 математического
ожидания
нормально
распределенного признака
по
выборочной средней
математического
ожидания
нормально
распределенного признака
по
выборочной средней 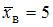 при
среднем квадратичном отклонении
при
среднем квадратичном отклонении 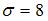 генеральной
совокупности использовали доверительный
интервал
,
где
–
значение аргумента функции Лапласа
,
при котором
,
–
объем выборки.
Установите
соответствие между значениями
надежности
и
соответствующим доверительными
интервалами, если
генеральной
совокупности использовали доверительный
интервал
,
где
–
значение аргумента функции Лапласа
,
при котором
,
–
объем выборки.
Установите
соответствие между значениями
надежности
и
соответствующим доверительными
интервалами, если 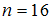 .
1.
.
1.
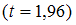 2.
2. 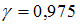
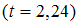
ОТВЕТ: 1) 1,08 <a<8,92
2) 0,52<a<9,48
Множество первообразных функции
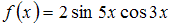 имеет
вид …
имеет
вид …
ОТВЕТ:
![]()
Дан доверительный интервал (24,6;26,8) для оценки математического ожидания нормально распределенного количественного признака при известном среднем квадратическом отклонении генеральной совокупности. Тогда при уменьшении объема выборки в четыре раза этот доверительный интервал примет вид …
ОТВЕТ: (23,5;27,9)
Для проверки нулевой гипотезы
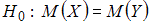 при
заданном уровне значимости
при
заданном уровне значимости 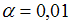 выдвинута
конкурирующая гипотеза
выдвинута
конкурирующая гипотеза 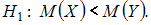 Тогда
область принятия гипотезы может иметь
вид …
Тогда
область принятия гипотезы может иметь
вид …
ОТВЕТ:
![]()
Мода равна 7, а медиана равна 9 для вариационного ряда …
ОТВЕТ: 1, 3, 7, 7, 9, 11, 12, 14, 15
Выборочное уравнение прямой линии регрессии Y на X имеет вид
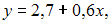 а
выборочные средние квадратические
отклонения равны:
а
выборочные средние квадратические
отклонения равны: 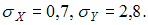 Тогда
выборочный коэффициент корреляции
равен …
Тогда
выборочный коэффициент корреляции
равен …
ОТВЕТ: 0,15
Производственная функция характеризуется неизменной отдачей от масштаба. Тогда параметры и могут принимать значения …
ОТВЕТ:
![]() ,
, ![]()
Дана функция спроса по цене
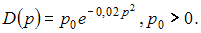 Тогда
спрос будет эластичным при …
Тогда
спрос будет эластичным при …
ОТВЕТ:
![]()
