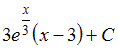5.Производная второго порядка функции равна …

6.Производная функции   равна …

7.Значение частной производной   функции 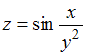  в точке 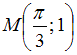  равно …

8.Площадь фигуры, изображенной на рисунке равна …

9.Система 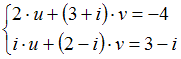  решается методом Крамера по формулам  ,  . Тогда вспомогательный определитель   равен …

10.Комплексное число задано в показательной форме   Тогда его тригонометрическая форма записи имеет вид …

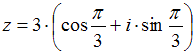
11.Если   и   – комплексно-сопряженные числа, то действительная часть функции  , при  , будет равна …

12.Все точки   комплексной плоскости, принадлежащие множеству  , изображенному на рисунке,

13. Предел числовой последовательности   равен …

2

14.Общее уравнение плоскости, проходящей через точку   параллельно плоскости  , имеет вид …

15.Соотношение 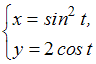   в прямоугольной декартовой системе координат задает …

Параболу

16.Прямые   и   …

Перпендикулярны

17.Функцией, ортогональной к функции   на  , является …

18.Наименьший положительный период функции   равен …

19.Модуль скорости точки, совершающей гармонические колебания, с амплитудой  , угловой частотой   и начальной фазой  , в момент времени   равен …

20.Определитель 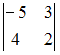  равен 

 – 22

21. Матрица  , где 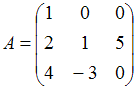 и  . Тогда элемент   равен …

 10

22.Канонический вид квадратичной формы   может иметь вид …

23.Сумма числового ряд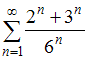а   равна …

24.Предел числовой последовательности 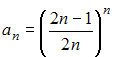  равен

25.Функцией, ортогональной к функции   на [-љЫ 1], является …

26.Амплитуда гармонических колебаний равна  ; угловая частота равна   рад.; а начальная фаза равна  . Тогда смещение колеблющейся точки от нулевого положения при   составляет …

27.Если   и   являются решением системы линейных уравнений 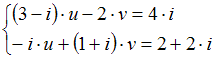 , то   равно …

28.Для функции 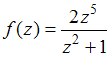  точка   является …

полюсом третьего порядка

29.Даны матрицы 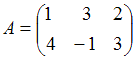 ,  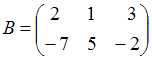. Тогда матрица   равна …

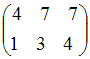
30. Умножение матрицы A на матрицу B  возможно, если эти матрицы имеют вид …

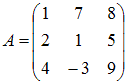 и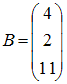 

31.Матрице 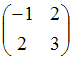  соответствует квадратичная форма  , равная …

32.Уравнение прямой, проходящей через точку пересечения прямых   и   перпендикулярно прямой   имеет вид …

33.Частная производная   функции   имеет вид …

34.Предел    равен …

0

35.Производная функции   равна …

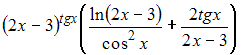
36.Общий член числовой последовательности    имеет вид 

37.Радиус сходимости степенного ряда   равен …

38.Даны числовые ряды: А) 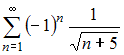 , В)  . Тогда …

ряд А) сходится условно, ряд В) сходится абсолютно

39.Корень уравнения 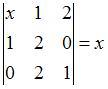  равен …

– 3

40.Отрицательно определенная квадратичная форма может иметь вид …

41. Угол   между прямой    и плоскостью   равен …

42.Поверхность   пересекается с плоскостью   по …

Параболе

43.Множество первообразных функции   имеет вид …

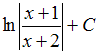
44.Предел 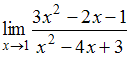  равен …

-2

45.Если   и   – комплексно-сопряженные числа, то мнимая часть функции  , где  , имеет вид …

46.Плоскости   и   перпендикулярны при значении  , равном …

47. Даны прямая линия  , заданная уравнением  , и плоскость  , заданная уравнением  . Тогда прямая  …

параллельна плоскости 

48.Центр сферы   имеет координаты …

49.Единственное решение имеет однородная система линейных уравнений …

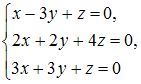
50.Квадратичная форма, не являющаяся знакоопределенной, может иметь вид …

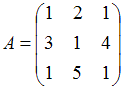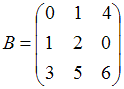51. Даны матрицы   и  . Если  , то след матрицы   равен …

11

52. Число особых точек функции 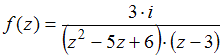  равно …

2

53.Система 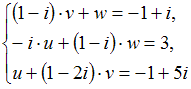  решается методом Крамера по формулам  ,  ,  . Тогда вспомогательный определитель   равен …

54.Если   и   – комплексно-сопряженные числа, то действительная часть функции  , где  , имеет вид …

55.Область определения функции 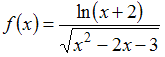  имеет вид …

56.Множество первообразных функции   имеет вид …

57.Предел 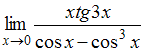  равен …

3

58.Горизонтальная асимптота графика функции 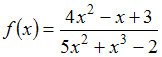  задается уравнением вида …

59.Радиус сходимости степенного ряда   равен …

60.На  линейном пространстве   задана операция …

  , для любого  , 

61.Корень уравнения 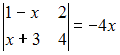  равен …

– 1

62. Канонический вид квадратичной формы   может иметь вид …

63.Даны матрицы 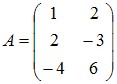 ,  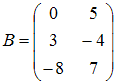. Тогда матрица   равна …

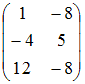
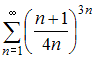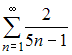64.Даны числовые ряды: А)  , В)  . Тогда …

 ряд А) сходится, ряд В) расходится

65.Каноническое уравнение прямой 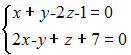  может иметь вид …

66. Все точки   комплексной плоскости, принадлежащие множеству  , изображенному на рисунке:

67.Модуль комплексного числа   равен …

2

68.Дана функция  . Тогда   равно …

69.Для функции 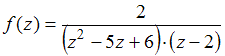  точка   является …

полюсом второго порядка

70.Произведение комплексных чисел   и 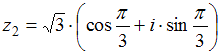  равно …

71.Предел 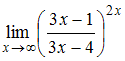  равен …

72.Множество первообразных функции   имеет вид