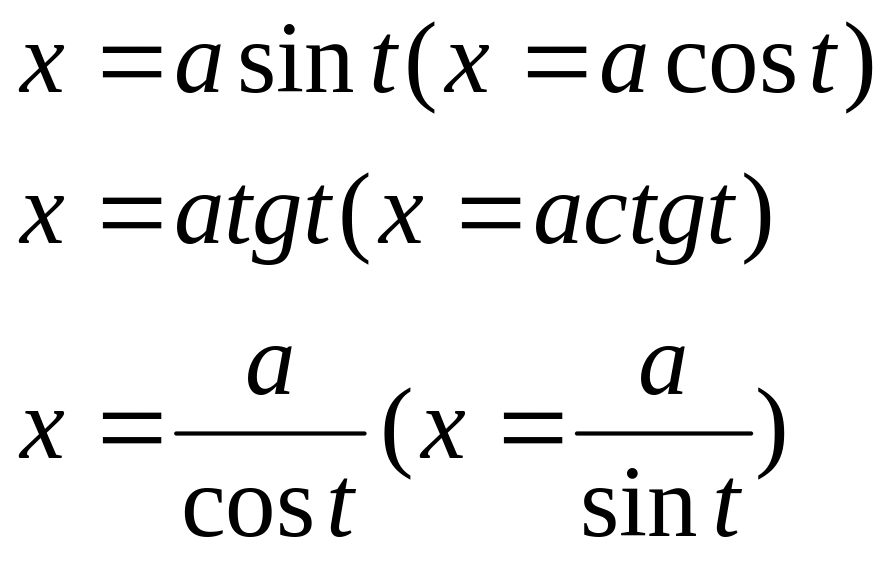Правило «трех сигм»
Если случайная величина имеет нормальное распределение, то отклонение этой величины от математического ожидания по абсолютной величине не превосходит утроенного среднего квадратичного отклонения.
Таким образом,
если Х
– нормально распределенная случайная
величина, то с вероятностью, близкой к
1(т.е. практически достоверно) можно
утверждать, что все ее значения
принадлежат промежутку
или
.
Графическая иллюстрация:
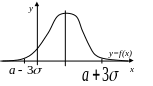
Задача. Известно, что средний расход удобрений на один га пашни составляет 80кг, а среднее квадратическое отклонение расхода составляет 5кг. Считая расход удобрений нормально распределенной случайной величиной, определить диапазон, в который вносимая доза удобрений попадет с вероятностью 0,999.
Решение. Т.к.
вероятность близка к 1, то для решения
задачи применяем правило «трех сигм»:
.
Следовательно, практически достоверно можно утверждать, что вносимая доза удобрений находится в диапазоне от 65кг до 95кг.
Заключение.
Цель данного руководства - оказание помочи студентам специальности «Ветеринария» в изучении дисциплины «Математика». Для этого в руководстве изложены цели и задачи дисциплины, ее трудоемкость, учебные планы по основным видам учебных занятий, а также сформулированы требования к уровню подготовленности студентов. Перечислено, какими знаниями и умениями должен владеть студент после изучения основных разделов дисциплины. Задачи, предложенные для самостоятельной работы, имеют два уровня сложности: I – основной, содержит типовые задачи по предложенным разделам. Задачи II уровня более сложные, их решение требует применения комплекса знаний из различных разделов или переноса знаний в нестандартную ситуацию.
В данном руководстве рассмотрены образцы решения типовых задач лишь по некоторым темам разделов, но в рекомендуемой литературе (п. 3.2.) приведено достаточное количество примеров с решениями.
ПРИЛОЖЕНИЯ
Приложение 1. Таблица производных
Функция
|
Производная функции |
С, где С-const |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Приложение 2. Таблица основных интегралов
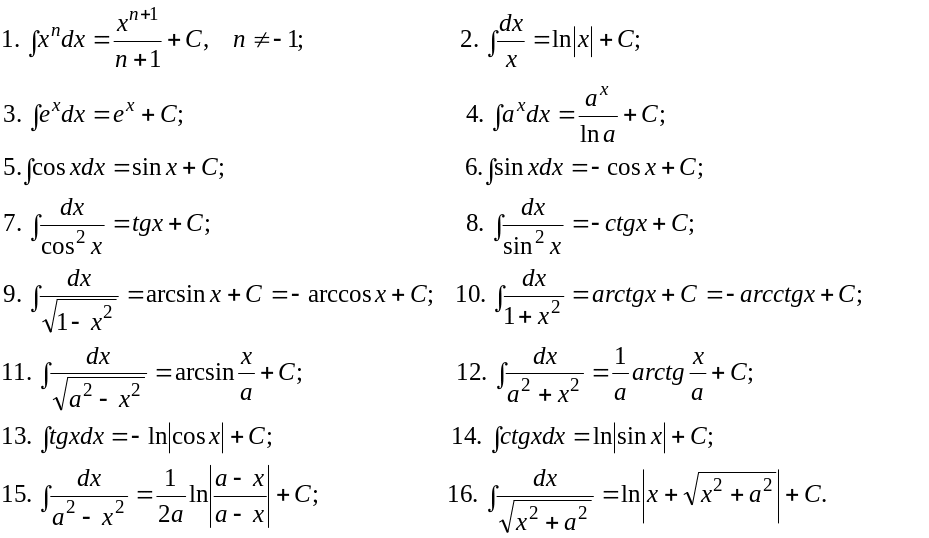
Приложение 3. Приемы вычисления некоторых видов интегралов.
Вид интеграла
|
Метод интегрирования
|
1.
|
Подстановка
|
2.
|
Интегрирование по частям по формуле
|
3.
|
Выделение полного квадрата
|
4.
|
Рекуррентная формула
|
5.
|
Тот же, что в интеграле вида 3,после чего получается интеграл вида 4
|
6. |
Выделение целой части, разложение
знаменателя на множители вида
|
7.
|
Универсальная подстановка
|
,
где
.
Метод интегрирования по частям
применяется, например, к интегралам
вида
,
где
- многочлен (в частности, степенная
функция
),
а
- одна из следующих функций:
,
,
,
,
,
,
а также к интегралам от произведений
показательной функции на косинус
или
синус.
затем подстановка
и
,
затем разложение
на простейшие дроби
или, если
,
подстановка
;
если
,
подстановка
;
если
,
подстановка
;
если
,
подстановка
8. Интеграл произведения синусов и
косинусов, например
|
Разложение подынтегральной функции
по формулам:
|
|
9.
|
Если m -нечетное
положительное число, то подстановка
n-нечетное положительное, то подстановка |
|
10. четное отрицательное |
Подстановка |
|
11. числа |
Применение формул
|
|
12. |
Подстановка
|
|
13. |
Подстановка
|
|
14.
|
Выделение полного квадрата под радикалом,затем линейная подстановка
|
|
15.
|
Обратная подстановка
|
|
16.
|
Сведение к интегралам вида 7 подстановкой
|
|
17.
|
Выделение полного квадрата под радикалом, затем линейная подстановка, приводящая к интегралам вида 16 |
|
18.
|
При
|
|
,
,
если
четные неотрицательные
общее
наименьшее кратное показателей всех
радикалов, под которыми
входит в подынтегральную функцию
общее
наименьшее кратное показателей всех
радикалов, под которыми x
входит в подынтегральную функцию
приводящая к интегралам вида 14
целом положительном - формула бинома
Ньютона и непосредственное интегрирование;
при
целом отрицательном,
,
,
- подстановка
;
при
целом - подстановка
;
при
целом - подстановка
