
- •Введение
- •Раздел 1. Роль и место математики в системе профессиональной подготовки студентов специальности « ветеринария»
- •1.1. Цели и задачи дисциплины
- •1.2. Структура и трудоемкость дисциплины
- •Примерная трудоемкость основных разделов дисциплины
- •Раздел 2. Примерные тематические планы по основным видам учебных занятий
- •2.1. Примерный тематический план лекционных занятий
- •2.1. Примерный тематический план практических занятий
- •2.3. Перечень тем для самостоятельной работы
- •Примерный перечень рефератов.
- •Раздел 3. Содержание основных разделов дисциплины и рекомендуемая литература
- •3.1. Содержание основных разделов дисциплины и требования к уровню подготовленности студентов.
- •2. Введение в математический анализ.
- •3. Дифференциальное исчисление.
- •4. Дифференциальное исчисление функций многих переменных.
- •5. Интегральное исчисление. Неопределенный интеграл.
- •6. Дифференциальные уравнения (ду).
- •7. Аналитическая геометрия.
- •Линейная алгебра.
- •9. Элементы теории вероятностей. Случайные события.
- •10. Дискретные и непрерывные случайные величины.
- •11. Элементы математической статистики.
- •3.2. Список рекомендуемой литературы
- •1. Основная литература
- •2. Дополнительная литература
- •Раздел 4. Примерные варианты контрольных работ по основным разделам дисциплины Тест по школьному курсу математики
- •1. Контрольная работа по теме «Введение в математический анализ. Дифференциальное исчисление функции одной независимой переменной»
- •2. Контрольная работа по теме «Интегральное исчисление. Дифференциальные уравнения»
- •3. Контрольная работа по теме « Случайные события»
- •4. Контрольная работа по теме «Случайные величины»
- •Тест по всем разделам дисциплины (с вариантами ответов для самопроверки)
- •Вопросы для подготовки к экзамену
- •Раздел 5. Образцы решения типовых задач Введение в математический анализ. Дифференциальное исчисление функции одной переменной.
- •Теория вероятностей.
- •Правило «трех сигм»
- •Приложение 1. Таблица производных
- •Приложение 2. Таблица основных интегралов
- •Приложение 4. Значение функции
- •Приложение 5. Значение функции
Раздел 5. Образцы решения типовых задач Введение в математический анализ. Дифференциальное исчисление функции одной переменной.
1. Вычислить указанные пределы:
![]()
![]()
![]()
Решение. 1) Разделив
числитель и знаменатель дроби на старшую
степень
![]() ,
получим:
,
получим:
![]() =
=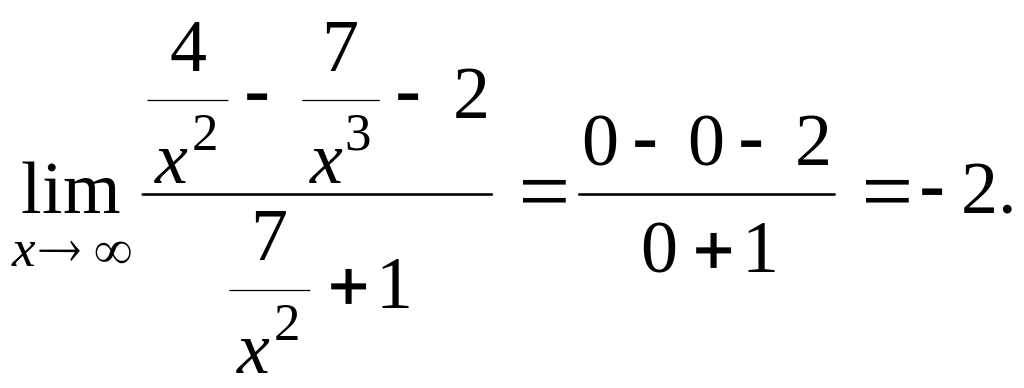
2) Старшая степень
в этом примере
![]() ,
поэтому числитель и знаменатель разделим
на x:
,
поэтому числитель и знаменатель разделим
на x:
![]()
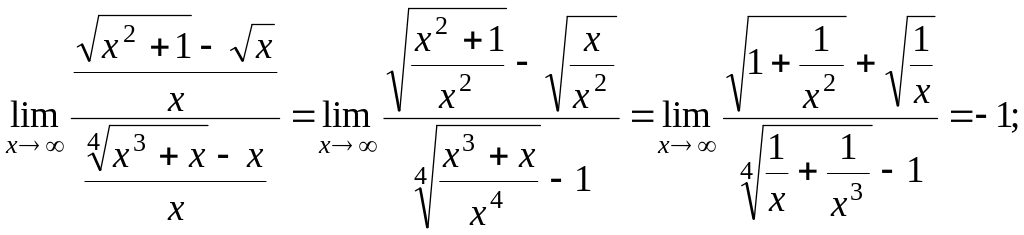
![]()
4) Найдём корни
трёхчленов:
![]()

![]()
5) Умножим числитель и знаменатель дроби на сопряженные им выражения
![]()
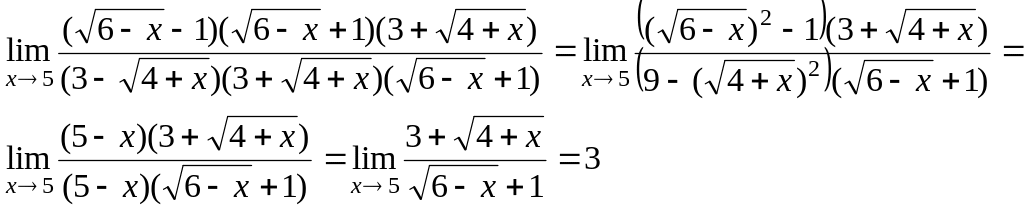
6)
![]()
2. Используя правила вычисления производных и таблицу, найдите производные следующих функций:

![]()
![]()
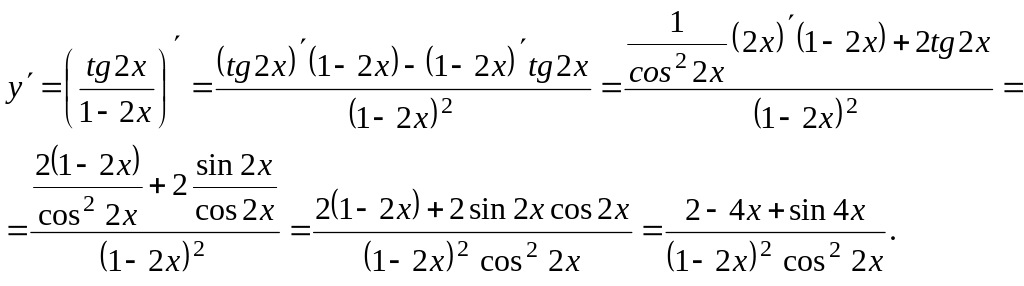
5)![]() ,
y=
,
y= .
.
6) y=cos2(x2),
y=![]() .
.
7)![]() ,
y=
,
y=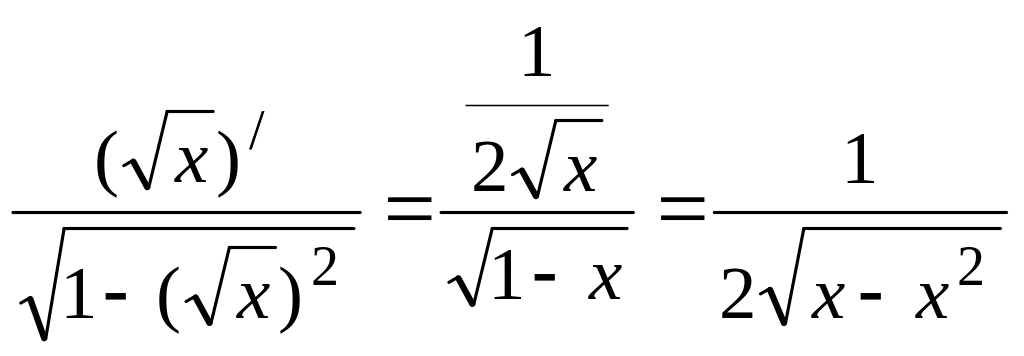 .
.
8)![]() ,
y=
,
y=![]() .
.
Интегральное исчисление.
В математическом анализе разработан ряд методов для вычисления неопределённых интегралов: непосредственное (табличное) интегрирование, метод подстановки, интегрирование по частям.
I. Метод непосредственного (табличного) интегрирования.
Использование
данного метода основано на применении
свойств
![]()
![]() и таблицы простейших интегралов
(Приложение 2). При вычислении интегралов
в этом случае нужно подынтегральную
функцию представить в виде суммы.
и таблицы простейших интегралов
(Приложение 2). При вычислении интегралов
в этом случае нужно подынтегральную
функцию представить в виде суммы.


II. Интегрирование подстановкой.
Этот метод основан на замене переменной интегрирования с целью сведения данного интеграла к такому виду, что его можно вычислить непосредственным интегрированием. Справедлива следующая формула:
![]() ,
где
,
где
![]() непрерывная
на интервале (а; в) функция, а
непрерывная
на интервале (а; в) функция, а
![]() -
непрерывно дифференцируема на интервале
-
непрерывно дифференцируема на интервале
![]() ,
причём функция
,
причём функция
![]() отображает интервал
в
интервал (а; в).
отображает интервал
в
интервал (а; в).
![]()
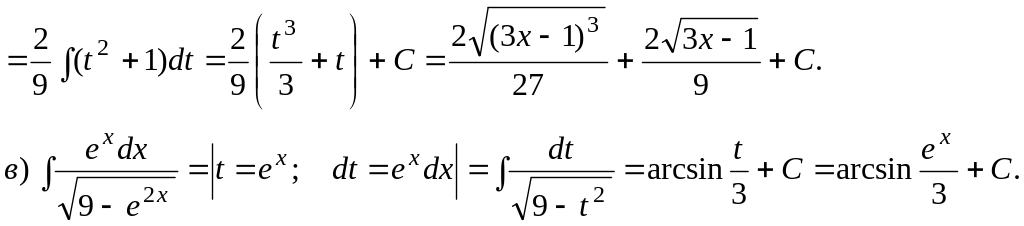
Теория вероятностей.
Основные задачи, связанные с нормальным распределением
Вычисление вероятности попадания в заданный интервал нормально распределенной случайной величины.
Вероятность
попадания нормально распределенной
случайной величины в интервал
![]() вычисляется
по формуле:
вычисляется
по формуле:
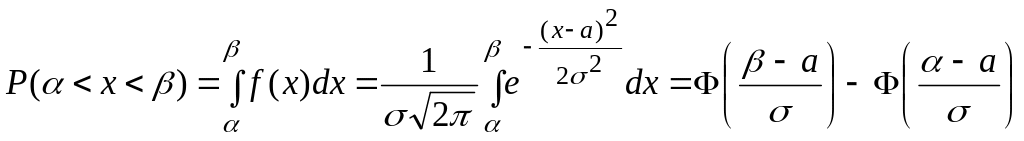 ,
где
,
где
![]()
![]() – функция Лапласа.
– функция Лапласа.
Задача. Средняя масса плода яблони сорта Мелба равна 160г, отклонение массы плодов от средней величины составляет 40г. Найти:
а) вероятность того, что масса наугад взятого яблока этого сорта будет находиться в пределах от 190г до 220г;
б) процент яблок не превосходящих по массе 140г;
в) величину, которую не превзойдет масса яблок с вероятностью 0,78.
Решение.
а) по условию
![]() г,
г,
![]() 220г,
а=160г,
220г,
а=160г,
![]() =40г.
=40г.
 .
.
б) вычислим
вероятность того, что масса яблок не
превзойдет 140г. По условию
![]() =0,
=0,
![]() =140.
=140.
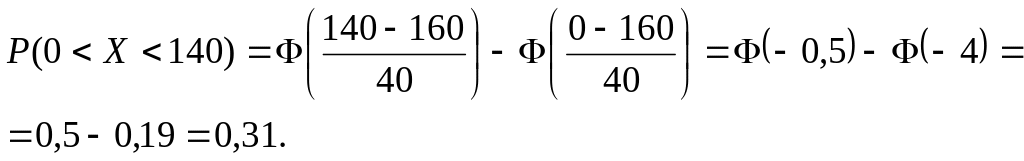
Следовательно, 31% яблок не превзойдет по массе 140г.
в) по условию
![]() .
.
![]()
т.к.
![]() ,
то
,
то
![]() .
В таблице по значению функции
.
В таблице по значению функции
![]() ,
определили, что значение выражения
,
определили, что значение выражения
![]() =0,77,
=0,77,
![]() .
.
Следовательно, можно утверждать, что масса яблок не превзойдет 190,8г с вероятностью 0,78.
Вычисление вероятности отклонения абсолютного значения случайной величины от наперед заданного числа.
Напомним, что
разность х-а
называется отклонением случайной
величины от математического ожидания.
Зададим положительное число
![]() .
Неравенство
.
Неравенство
![]() равносильно двойному неравенству
равносильно двойному неравенству
![]() .
.
Вероятность того,
что отклонение абсолютного значения
нормально распределенной случайной
величины меньше положительного наперед
заданного числа
![]() ,
вычисляется по формуле:
,
вычисляется по формуле:
![]() .
.
Замечание.
Очевидно, что события, описываемые
неравенствами
и
![]() –
противоположные, следовательно, если
вероятность появления события,
описываемого неравенством
равна р,
то вероятность события, описываемого
неравенством
,
равна 1-р.
–
противоположные, следовательно, если
вероятность появления события,
описываемого неравенством
равна р,
то вероятность события, описываемого
неравенством
,
равна 1-р.
Задача. Подшипники, изготавливаемые автоматом, считаются стандартными, если отклонение посадочного диаметра подшипника от проектного размера не превышает 0,2мм. Случайное отклонение посадочного диаметра подчинено нормальному закону с математическим ожиданием а =0 и средним квадратичным отклонением =0,08мм. Сколько процентов стандартных подшипников изготавливает автомат?
Решение.
![]()
Итак, 98,76% стандартных подшипников изготавливает автомат.
