Г л а в а 2

Дифференциальное исчисление функции одной переменной

§ 1. Производная

1.1. Понятие производной. Физический и геометрический смысл производной. Рассмотрим некоторую функцию . Эта функция определена и непрерывна на множестве Следовательно, всякому значению аргумента соответствует значение функции . Если получит приращение , аргумент примет значение и соответственно изменится функция, приняв значение При этом приращение функции будет равно разности то есть Таким образом у всякой непрерывной функции приращение аргумента на сопровождается приращением функции на . При этом отношение дает величину среднего приращения функции при единичном приращении аргумента на интервале , то есть представляет собой среднюю скорость изменения функции на рассматриваемом интервале. Чем меньше тем в большей степени средняя скорость изменения функции соответствует истинной скорости изменения функции в точке . Предельное значение отношения при стремящемся к нулю, дает истинную скорость изменения функции в точке называемую производной функции . Обозначается

С геометрической точки зрения первая производная функции представляет собой угловой коэффициент касательной к графику функции в точке дифференцирования.

Д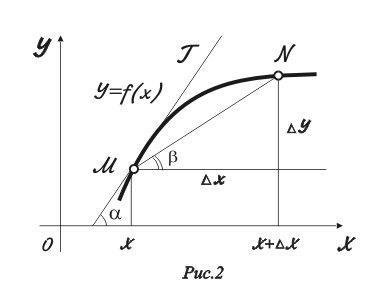 ействительно, (рис. 2), где — угол наклона секущей к оси OX. При точка N приближается к точке М, стремясь с ней слиться, то есть секущая вырождается в касательную  а угол превращается при этом в угол Угол – угол наклона касательной к оси представляет собой предельное значение угла наклона секущей  , Таким образом, оказывается, что угловой коэффициент касательной равен . А поскольку то Итак, имеем

Производная функции , рассматриваемая на множестве тех точек, где она существует, сама является функцией. Производная от этой функции называется производной 2-го порядка от функции , . Аналогично определяется производная 3-го порядка. и т. д.

1.2. Таблица производных основных элементарных функций

1.	5.
2.	6.
3.	7.
3а.	8.
4.	9.

1.3. Правила дифференцирования функций

Пусть – постоянная и , –дифференцируемые функции, тогда:

1. 2. 3.

4. 5.

6. Дифференцирование сложной функции. Если где то есть сложная функция от Рассматриваемая сложная функция представляет собой результат последовательного наложения на независимую переменную двух^) функций – и . Чтобы получить у, нужно произвести над аргументом операции, соответствующие функции , а над полученным результатом – операции, предписываемые функцией .

Пусть функция имеет производную в точке x, а функция имеет производную в точке Тогда сложная функция имеет производную в точке х , равную (1)

Таким образом, чтобы найти производную сложной функции, достаточно перемножить производные функций, входящих в состав сложной функции.

Например, найдем производную функции .

Заданная функция является результатом наложения на аргумент двух функций – арксинуса и логарифма. Полагая и , имеем и, согласно (1), где и Отсюда получаем

7. Дифференцирование обратной функции. Пусть функция имеет обратную . Тогда производная обратной функции равна

(2)

Например, известно, что , нужно найти производную функции

– функция обратная заданной , поэтому, согласно (2), имеем .

8. Дифференцирование неявной функции. Выше было рассмотрено дифферен-цирование явных функций, заданных в виде Рассмотрим неявную функцию заданную уравнением Для нахождения производной , нужно продифференцировать обе части уравнения по x, рассматривая переменную как функцию от , а затем полученный результат разрешить относительно производной Например, найдем производную , если функциональная связь задана неявно уравнением и вычислим значение производной в точке Дифференцируя обе части уравнения, описывающего функциональную связь переменных и , и учитывая, что есть функция от , получим откуда Значение производной в точке получим, подставив в выражение производной

Дифференцируя обе части равенства и учитывая, что есть функция от , получим откуда

Рассмотрим некоторые задачи.

Пример1. Составить уравнения касательной и нормали к кривой в точке ( 2, 4 ).

 Касательная – это прямая, имеющая с графиком функции единственную общую точку и угловой коэффициент , следовательно, ее уравнение будет иметь вид

Найдем производную в точке : . Согласно геометрическому свойству производной, есть угловой коэффициент касательной, проведенный к заданной кривой в точке ( 2, 4 ).

Таким образом, имеем уравнение касательной или

Чтобы получить уравнение нормали, воспользуемся тем, что нормаль перпендикулярна касательной, значит произведение их угловых коэффициентов равно минус единице, то есть . А поскольку то . В условиях рассматриваемой задачи . Так как уравнение всякой прямой, проходящей через точку , имеет вид а нормаль – одна из этих прямых, то имеем ее уравнение или .◄

Пример2. На кривой найти точки, в которых касательная:

а) параллельна прямой

б) перпендикулярна к прямой

 Для отыскания требуемых точек принимаем во внимание тот факт, что угловой коэффициент касательной равняется значению производной функции в точке касания, то есть

а) из условия параллельности прямых следует, что угловой коэффициент касательной равен угловому коэффициенту заданной прямой, то есть , откуда . Следовательно, касательная к кривой будет параллельна прямой если касательная проведена в точках

б) из условия перпендикулярности следует, что то есть откуда Значит в точках касательная к заданной кривой будет перпендикулярна прямой ◄

Пример3. Спрос как функция цены описывается соотношением Выяснить, какова скорость изменения функции спроса при

 Скорость изменения функции в некоторой точке равна первой производной функции в этой точке. Следовательно, искомая величина представляет ни что иное, как . Скорость изменения функции спроса отрицательна. ( О чем говорит отрицательная скорость изменения функции? ) ◄

В №№ 38 - 57 вычислить производную и ее значение в точке .

38. 39.

40. 41.

42. 43.

44. 45.

46. 47.

48. 49.

50. 51.

52. 53.

54. 55.

56. 57.

В №№ 58 - 63 для заданных функций найти и .

58. 59. 60.

61. 62. 63.

В №№ 64 - 66 найти производную неявно заданной функции.

64. 65.

66. 67.

В №№ 68 - 73 написать уравнения касательной и нормали к графику функции точке .

68. 70.

72. 69.

71. 73.

74. Найти коэффициенты и в уравнении параболы , касающейся прямой в точке .

75. Показать, что касательные к гиперболе в точках ее пересечения с осями координат параллельны между собой.

76. Составить уравнение нормали к графику функции в точке пересечения с биссектрисой первого координатного угла.

77. Cоставить уравнение такой нормали к параболе , которая перпендикулярна к прямой, соединяющей начало координат с вершиной параболы.

78. Закон движения материальной точки по прямой имеет вид

а) В какие моменты времени точка находится в начале координат?

б) В какие моменты времени направление ее движения совпадает с положительным направлением оси Ох?

в) В какие моменты времени ее ускорение равно нулю?

79. Тело массой 4г движется прямолинейно по закону Определить кинетическую энергию тела в момент времени с.

80. В какой момент надо устранить действие сил, чтобы точка, участвующая в гармоническом колебании , продолжала двигаться равномерно со скоростью

81. Радиус шара изменяется со скоростью . С какой скоростью изменяется объем и поверхность шара?

82. Колесо вращается так, что угол поворота пропорционален квадрату времени. Первый оборот был сделан колесом за время с. Найти угловую скорость в момент времени с после начала движения.

83. Скорость прямолинейного движения тела пропорциональна квадратному корню из пройденного пути (как, например, при свободном падении тела). Доказать, что тело движется под действием постоянной силы.