1. Умова задачі

Для заданої плоскої шарнірно-стрижневої статично невизначної системи (рис. 1, а, б) виконати розрахунок на міцність методом допустимих напружень при умові, що всі стрижні виконані з одного матеріалу і мають однакові площі поперечних перерізів, які рівні А.

Матеріал стрижнів – сталь Ст. 3, [σ]=160 МПа, Е=2·10⁵ МПа.

Числові дані взяти з таблиці.

Порядок розрахунку:

1. Нарисувати схему в масштабі.

2. Встановити ступінь статичної невизначності системи.

3. Розглянути статичну, геометричну і фізичну частини задачі і визначити поздовжні сили N_i в елементах системи, а також нормальні напруження σ_i у їх поперечних перерізах в залежності від зовнішнього навантаження F, заданого в загальному вигляді.

4. Визначити величину допустимого навантаження [F], виходячи з умови міцності методу допустимих напружень.

5. Визначити нормальні напруження σ_і у поперечних перерізах стрижнів системи при F=[F].

Числові значення геометричних параметрів і складових навантаження

№ варіанту	Розміри системи, м				Площа А, см2		Δt, град.		Δ, мм
	a	b	c	d
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25	4,0 3,8 3,6 3,4 3,2 3,0 2,8 2,6 2,4 2,2 2,0 1,8 1,6 1,4 1,2 2,0 2,2 2,4 2,6 2,8 3,0 2,2 2,4 2,6 2,8	1,8 1,9 2,0 2,1 2,2 3,2 2,4 2,6 2,8 3,0 3,2 3,4 3,6 3,8 4,0 3,8 3,6 3,2 3,0 2,8 2,6 1,4 2,2 2,0 2,8	1,4 1,8 2,2 2,4 2,6 2,1 2,3 2,5 2,7 2,9 3,1 3,3 3,5 3,7 3,9 3,7 3,5 3,3 3,1 2,9 2,7 2,5 2,3 2,1 1,9	1,0 1,2 1,4 1,6 1,8 2,0 1,0 1,2 1,4 1,6 1,8 1,6 1,4 1,2 1,0 1,2 1,4 1,6 1,8 2,0 1,5 1,0 1,2 1,4 1,6		2,0 2,2 2,4 2,6 2,8 3,0 3,2 3,4 3,6 3,8 4,0 4,2 4,4 4,6 4,8 5,0 4,8 4,6 4,4 4,2 4,0 3,8 3,6 3,4 3,2		+30 -40 +50 -60 +70 -80 +20 +60 -50 -40 -30 +40 -50 -60 +70 +80 -70 +60 +50 -40 -30 +30 -40 +50 -60		-0,2 +0,3 -0,4 +0,5 -0,6 +0,7 -0,8 -0,9 +1,0 +1,2 +1,3 -1,4 +1,5 +1,4 -1,3 -1,2 +1,1 -1,0 -0,9 +0,8 +0,7 -0,6 +0,5 -0,4 +0,3

2. Основні теоретичні відомості

Система, яка складається з стрижнів, що з’єднані між собою шарнірами, називається шарнірно-стрижневою системою. Якщо осі елементів системи розташовані в одній площині, то така система називається плоскою шарнірно-стрижневою системою. В елементах шарнірно-стрижневої системи виникають поздовжні сили. Для визначення цих сил використовують метод перерізів. Вирізають окремі частини системи (вузли або абсолютно жорсткі стрижні) і для них складають рівняння рівноваги. Якщо для визначення поздовжніх сил в елементах системи рівнянь рівноваги достатньо, то така система називається статично визначною. Якщо ж внутрішніх сил в елементах системи є більше, ніж можна скласти рівнянь рівноваги для даної системи, то така система називається статично невизначною. Різниця між кількістю поздовжніх сил, що виникають в елементах системи, і кількістю рівнянь статики, які можна скласти для даної системи, називається ступенем статичної невизначності даної системи.

Зауважимо, що у відповідних розділах опору матеріалів і будівельної механіки подаються загальні методи розрахунку статично невизначних стрижневих систем. Тут викладається часткова методика розрахунку стрижневих статично невизначних систем, елементи яких працюють в умовах розтягу чи стиску. Згідно цієї методики послідовно розглядається три частини задачі: статична, геометрична і фізична. Статична частина задачі полягає в складанні рівнянь статики для даної системи і встановлення ступеня її статичної невизначності, тобто числа «зайвих» зв’язків. Суть геометричної частини задачі полягає в тому, що виходячи із цілісності системи після прикладання навантаження, розглядають її переміщення і складають додаткові рівняння – рівняння сумісності деформацій. Кількість цих рівнянь рівна ступеневі статичної невизначності системи. Фізична частина задачі включає використання фізичного співвідношення – закону Гука, з допомогою якого деформації в рівняннях сумісності виражаються через відповідні поздовжні сили. Із отриманих таким чином рівнянь і рівнянь статики визначаються зусилля в елементах системи.

На відміну від розрахунку статично визначних систем зусилля в елементах статично невизначної системи залежать від співвідношення між жорсткостями її елементів. Чим більша жорсткість елемента, тим більшу частину навантаження він сприймає. Жорсткість стрижня при розтягу-стиску визначається за формулою

, (1)

де Е – модуль Юнга матеріалу стрижня, l – довжина стрижня, А – площа його поперечного перерізу.

Отже, шляхом зміни довжин елементів, площ їх поперечних перерізів, їх матеріалів можна добиватися більш рівномірного розподілу зусиль, що виникають в елементах системи.

При розв’язуванні задачі використовується закон Гука при розтягу-стиску стрижня:

, (2)

Δl – абсолютна лінійна деформація стрижня; N – поздовжня сила в стрижні.

У статично невизначних системах внутрішні зусилля виникають і при зміні температури її елементів. Закон Гука з врахуванням зміни температури є таким

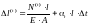, (3)

де Δt – зміна температури; Δl^(t), N^(t) – абсолютне лінійне видовження і поздовжня сила в стрижні, зумовлені зміною температури; α_t – температурний коефіцієнт лінійного розширення матеріалу стрижня.

Додаткові внутрішні зусилля у статично невизначних системах можуть виникати і внаслідок монтажу системи з неточно виготовлених елементів (дійсна довжина елемента відрізняється від проектної, зміщена опора і т.п.). Вплив цих факторів враховується додатковими членами у рівняннях сумісності деформацій.

Розрахунок на міцність можна проводити методом допустимих напружень з використанням умови міцності

, (4)

де [σ] – допустиме нормальне напруження матеріалу; σ_max – максимальне нормальне напруження, що виникає в елементах системи.

Враховуючи, що

будемо мати:

, (5)

N_max – максимальне значення поздовжньої сили.

За формулою (5) проводиться перевірка міцності стрижня. Якщо необхідно підібрати площу поперечного перерізу стрижня, то із умови (5) випливає така формула для вибору площі

. (6)

При дії на систему силового навантаження, при зміні температури та наявності неточностей монтажу елементів системи сумарні напруження знаходять використовуючи принцип суперпозиції (при умові, що матеріал елементів системи підлягає закону Гука).