3. Приклад розв’язання задачі

Для заданої шарнірно-стрижневої системи (рис. 2), в якій брус AB абсолютно жорсткий, а інші стрижні виготовлені зі сталі і мають однакові площі поперечних перерізів A, потрібно провести розрахунок на міцність, в процесі якого визначити:

1. Зусилля у стрижнях системи.

2. Площу A поперечного перерізу стрижнів.

3. Напруження у стрижневих елементах системи.

4. Провести аналіз можливого зниження матеріалоємності системи.

Матеріал стрижнів – сталь 3: [σ]=160 МПа, Е=2·10⁵ МПа.

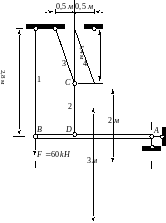
Рис. 2

Р о з в ’ я з а н н я

1. Знаходимо зусилля в елементах системи.

Статична частина задачі. Використовуючи метод перерізів, уявно розрізаємо стрижні, виділяючи окремі частини системи (вузол С, абсолютно жорсткий брус AB); прикладаємо у перерізах елементів системи поздовжні сили N₁, N₂, N₃, N₄, а також реакції в опорі A-Х_A, У_A (рис. 3. а, б).

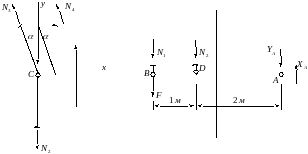
а) б)

Рис. 3

Складаємо рівняння рівноваги для вузла С (як для збіжної плоскої системи сил):

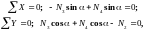(7)

а також для бруса АВ (як для довільної плоскої системи сил):

; ; (8)

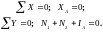; (9)

Рівняння (9) використовуються для визначення опорних реакцій Х_A і У_A.

Таким чином, для визначення чотирьох сил N₁, N₂, N₃, N₄, маємо тільки три рівняння. Отже, система один раз статично невизначна і потрібно скласти одне рівняння сумісності деформацій.

Геометрична частина задачі. Розглядаємо переміщення у системі після її навантаження силою F (рис. 4).

Внаслідок деформації стрижнів 1, 2, 3, 4 відповідно на Δl₁, Δl₂, Δl₃, Δl₄ абсолютно жорсткий брус АВ, залишаючись прямим, повернеться навколо точки А і займе положення АВ^′. Оскільки переміщення точок системи малі в порівнянні з розмірами її елементів, а горизонтальні складові переміщень точок В і D підвісу бруса АВ в свою чергу є величинами вищого порядку малості в порівнянні із вертикальними складовими цих переміщень, то це дозволяє вважати, що ці точки будуть переміщатися вертикально вниз (дуги ВВ^′ і DD^′ замінюємо перпендикулярами в точках В і D до початкового положення осі бруса АВ). Точка В переміститься вниз на величину, яка дорівнює видовженню стрижня 1-Δl₁; точка D – на величину, що складається з відрізка СС^′ – опускання вузла С і видовження стрижня 2-Δl₂. Опускання вузла С у свою чергу відбувається за рахунок видовження стрижнів 3 і 4

; .

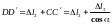З подібності трикутників АВВ^′ і АDD^′ знаходимо

,

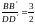або

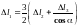. (10)

Отримане рівняння (10) і є рівнянням сумісності деформацій елементів системи.

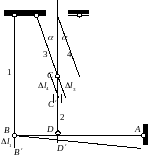
Рис. 4.

Фізична частиина задачі. Виражаємо деформації і Δl_і (і=1, 2, 3) у рівнянні (10) через відповідні сили, використовуючи закон Гука

,

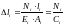де С_і – жорсткість і-го стрижня;

.

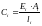Отже, рівняння (10) запишеться так:

,

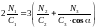або

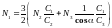. (11)

Розв’язуючи систему 3 лінійних алгебраїчних рівнянь, яка включає рівняння (7), (8), і (11), отримуємо:

;

;

.

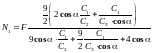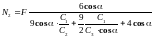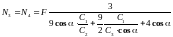Обчислюємо параметри системи:

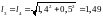м;

;

;

.

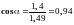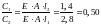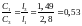У результаті отримуємо вирази для сил N_i (і=1, 2, 3) через силу F

;

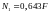; (12)

.

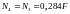2. Визначаємо площі поперечних перерізів стрижнів з умови (6).

Згідно з умовою задачі площі поперечних перерізів всіх стрижнів повинні бути однакові і рівні А. Тому максимальні напруження виникають у першому стрижні, оскільки в цьому стрижні діє найбільша поздовжня сила (12). З умови (6) отримуємо

,

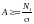звідки

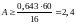см².

Зауважимо, що коли відомі площі поперечних перерізів стрижнів і потрібно визначити допустиме значення навантаження [F], то для цього необхідно використати залежність (5), з якої знаходимо допустиму величину навантаження.

3. Обчислюємо напруження, що виникають в інших стрижнях системи, і порівнюємо їх з допустимими напруженнями [σ]=160 МПа:

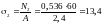кН/см² =134 МПа ;

кН/см² =71 МПа .

4. Напруження у стрижнях 2, 3, 4 є значно нижчими від допустимого, що свідчить про нераціональне використання матеріалу стрижнів, завищений коефіцієнт запасу міцності у них. Для більш рівномірного розподілу зусиль між елементами системи доцільно змінити співвідношення їх жорсткостей, збільшивши жорсткості елементів 2, 3, 4 або зменшивши жорсткість елемента 1.

ЗАДАЧА 2. РОЗРАХУНОК СТЕРЖНІВ ПРИ КРУЧЕННІ