1.2. Теоретические предпосылки, позволяющие понять, как в настоящее время характеризуют состояния электронов в атоме

Для понимания квантовой теории удобно сугубо математические параметры объяснять с точки зрения аналогий. Аналогии всегда полезны, поскольку они позволяют понимать новые взаимосвязи и запоминать основной ход рассуждений. Даже такой высокоодаренный математик, как Архимед, обращался к механическим аналогиям, когда хотел убедиться в справедливости некоторых математических теорем. Это вполне приемлемый способ мышления, поэтому и мы для обсуждения ряда сугубо математических понятий квантовой теории используем подходящие аналогии.

Представим в начале, для простоты, что находящийся в атоме электрон являет собой круглое твердое тело (шарик). Тогда, в соответствии с механикой Ньютона, и «планетарной» моделью его перемещения, электрон в атоме может участвовать в двух видах движения: в орбитальном движении относительно ядра (то есть в движении по орбите, подобно тому, как Земля движется вокруг Солнца) и в собственном вращательном движении (то есть, вращаясь вокруг своей оси). Соответственно, для полного описания состояния электрона в атоме в таком гипотетическом случае необходимо было бы знать следующие четыре параметра:

   1. Энергию электрона;

  2. Величину орбитального момента количества движения;

   3. Направление орбитального момента количества движения;

  4. Направление собственного момента количества движения.

Второй и третий параметры характеризуют движение электрона относительно ядра, а четвёртый описывает собственное вращательное движение электрона.

Но как уже говорилось, электрон наряду с корпускулярными свойствами проявляет и волновые свойства, поэтому его состояние нельзя представить как движение материальной частицы по какой-либо орбите. Квантовая механика рассматривает вероятность пребывания электрона в пространстве вокруг ядра. Тем не менее, и в квантовой теории считается, что состояние электрона в атоме тоже определяется четырьмя квантовыми числами. Формально число параметров одинаково, но при этом принципиально новым является квантование физических величин. В классической механике физические величины, характеризующие указанные 4 параметра, могли изменяться непрерывно (то есть, быть любым числом на всей числовой оси). В квантовой теории – энергия атома может принимать лишь определенные дискретные значения (иначе говоря, только определенные числа). По этой причине все эти четыре параметра, описывающие состояние электрона в атоме, вследствие волновых свойств должны принимать лишь квантованные (дискретные значения), то есть все их возможные значения обязательно должны быть пропорциональны определенным целым числам, называемым квантовыми. Слово «квант» означает «порция» - минимальное, неделимое более количество какое-либо физической величины.

Заметим, что в понимании окружающей действительности с античных времен противостояли друг другу два качественно различных принципа строения материи. Согласно одному из них материя непрерывна и бесконечно делима. Тогда как согласно второму существуют неделимые боле, дискретные порции материи, называемые атомами (напомним, что слово «атом» в свою очередь, означает «неделимый»).

До появления квантовой теории деление по этому принципу было умозрительным, поскольку отсутствовал критерий того, какую именно порцию вещества следует назвать неделимой. Поскольку материя на макроуровне никаких дискретных свойств не проявляет, законы классической физики были основаны на непрерывности и бесконечной делимости всех форм материи и ее характеристик. Квантовая теория определила, что природа устроена так, что в ней существует минимальная «порция» («квант») воздействия. Согласно идее Планка, универсальной количественной характеристикой минимального воздействия в природе служит постоянная Планка или иначе элементарный квант действия. Любое воздействие происходящее в природе, можно охарактеризовать целым числом квантов действия , так что постоянная Планка играет роль неделимой более «порции» воздействия. Поскольку она очень мала, то квантованность материи в макроскопических опытах себя не проявляет, что и выражается в наблюдаемой непрерывности воздействия в классической физике.

В квантовой теории для полного описания состояния электрона в атоме используются следующие 4 параметра.

1. Главное квантовое число соответствует порядковому номеру электронного слоя и характеризует величину энергии электрона; может принимать значения 1, 2, 3, 4, 5 , 6, 7. Значения соотносятся с обозначением атомных электронных слоев как показано в табл. 1.

Таблица 1.

Значение	1	2	3	4	5	6	7
Обозначение электронного слоя	K	L	M	N	O	P	Q

Электроны с образуют ближайший к ядру атома электронный слой (энергетический уровень). Электроны с образуют второй от атома электронный слой и т. д.

Поскольку в качестве квантово-механической модели электрона в атоме принято представление об электронном облаке, плотность соответствующих участков которого пропорциональна вероятности нахождения там электрона, то на рис. 4 показан график распределения плотности вероятности в зависимости от числа и от расстояния от ядра

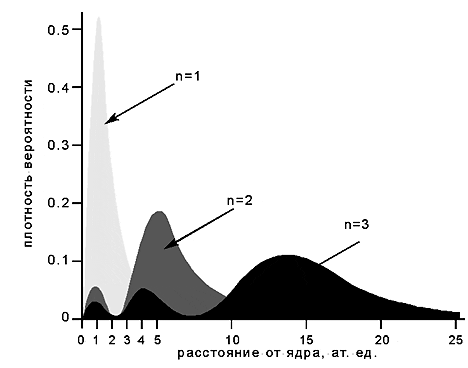
Рис. 4. Распределения плотности вероятности для электрона в зависимости от главного квантового числа

Рис.4 свидетельствует о том, что характерный размер атома при увеличении числа быстро растет. При этом электронное облако по мере возбуждения атома (увеличении числа ) как бы выталкивается к периферии (уходит подальше от ядра). Иначе говоря, чем прочнее электрон связан с ядром, тем меньше должно быть электронное облако по размерам и более плотным по распределению заряда.

Поскольку поведение электрона определяется кулоновским взаимодействием электрических полей и, следовательно, расстоянием от ядра (электроны ближнего слоя притягиваются ядром сильнее, а электроны дальнего слоя – слабее), то главное квантовое число n задаёт не только размер орбитали, но и энергию электрона. Главное квантовое число n определяет общую энергию электрона на данной орбитали (энергетический уровень):

,

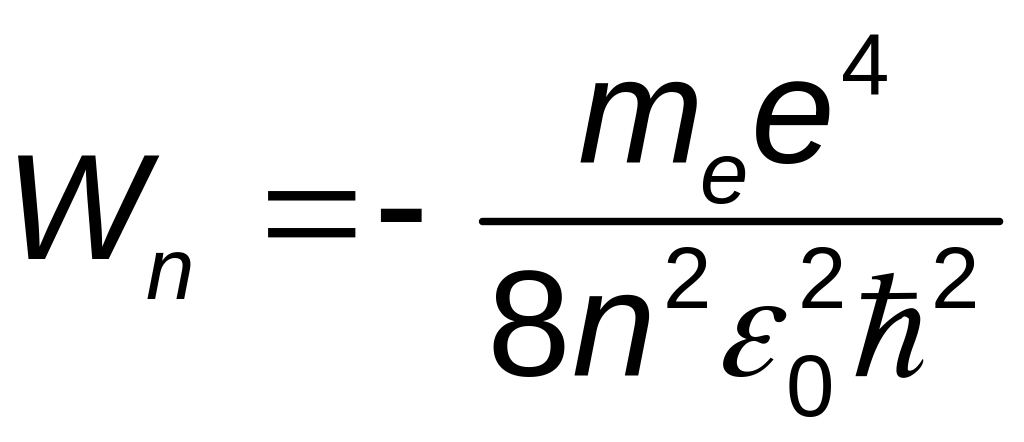где – масса электрона;

– элементарный электрический заряд;

- порядковый номер главного квантового числа;

– электрическая постоянная;

– постоянная Планка.

Энергия для n = ∞ соответствует энергии одноэлектронной ионизации для данного энергетического уровня.

2. Орбитальное (побочное) квантовое число l характеризует форму электронной орбитали (и, соответственно, энергетические подуровни) при заданном значении главного квантового числа .

Орбитальное число l может принимать значения целых чисел от 0 до .

Состояния электрона, которые характеризуются различными значениями числа l, называют энергетическими подуровнями.

Орбитальное квантовое число определяет также момент импульса электрона. Момент импульса при этом задаётся соотношением

.

В одной и той же оболочке (уровне) энергия подоболочек (подуровней) возрастает.

Орбитали с разным значением числа l обозначаются буквами s, p, d, f (табл. 2).

Таблица 2.

Значение числа l	0	1	2	3
Обозначение орбитали	s	p	d	f

Заметим, что эти буквы не являются сокращениями слов, описывающих «форму» орбитали. Исторически сложилось так, что первые четыре значения имеют буквенные символы, произошедшие от спектроскопических терминов, использованных в 1890-е годы при описании спектров щелочных металлов: 0-s (sharp-резкий), 1-p (principal-главный); 2-d (diffuse-диффузный); 3-f (fundamental-фундаментальный).

Обычно орбиталь графически изображают в виде поверхности, очерчивающей область, где вероятность появления электрона наибольшая, иначе говоря, электронная плотность максимальна. У атома водорода на первом электронном уровне находится только одна s-орбиталь. Эта орбиталь электрона имеет сферическую (шаровую) форму (рис.4а).Сферическая форма s-орбитали, свидетельствует об одинаковой электронной плотности в направлении каждой оси трехмерных координат.

Рис. 4а. Изображение s-орбитали сферическая формы

Для атома водорода, как мы видели, характерной формой орбитали была сфера. Оказалось, что наряду с круговыми орбиталями, у электрона возможны орбитали, подобные эллипсоидам с различным эксцентриситетом. Орбитальное квантовое число определяет форму поверхности максимальной вероятности нахождения электрона и ее симметрию.

Все s-орбитали (l = 0) сферические. P-орбитали (l = 1) имеют форму гантели; d-орбитали (l = 2) – четырехлепестковой розы и т. д. (рис.5).

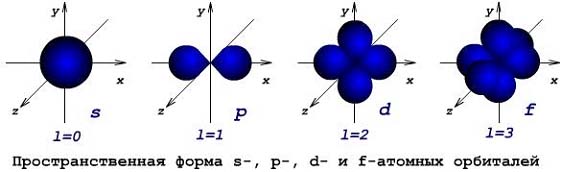
  Рис. 5. Изображение пространственной формы s-, p-, d- и f- электронных орбиталей 

Начиная со второго электронного уровня ( ) помимо s-орбитали появляются также три р-орбитали. Каждый энергетический уровень (слой), начиная с n=2, имеет три p-орбитали ( ). Все три р-орбитали расположены в атоме взаимно перпендикулярно (рис. 6). Они имеют форму объемных восьмерок (гантелей). Именно так выглядит область наиболее вероятного местонахождения электрона в районе атомного ядра. Каждая р-орбиталь расположена вдоль одной из трех взаимоперпендикулярных осей, в соответствии с этим в названии р-орбитали указывают с помощью соответствующего индекса ту ось, вдоль которой располагается ее максимальная электронная плотность.

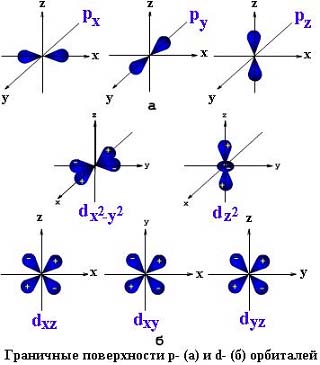
  Рис. 6. Изображение пространственной формы рх-, ру- и рz-орбиталей (а) и d-орбиталей (б)

Они направлены вдоль осей пространственных координат, поэтому их часто обозначают как рх-, ру- и рz-орбитали. Такое обозначение указывает на пространственную направленность р-орбиталей. Если рх-орбиталь расположена в направлении оси х, то, очевидно, рх-электрон с наибольшей вероятностью находится вблизи оси х. То же можно сказать и об орбиталях ру и pz. С увеличением n электроны занимают р-орбитали, расположенные на больших расстояниях от ядра, но направление по осям х, у, z всегда сохраняется. Еще более сложные формы (рис. 6, б), чем p-орбитали, имеют d-орбитали (их пять ).

Орбитали можно представить и в виде изображений поперечных сечений плотности вероятности (рис.7), величина которой отражена цветом (чёрный цвет соответствует минимальной плотности вероятности, а белый — максимальной).

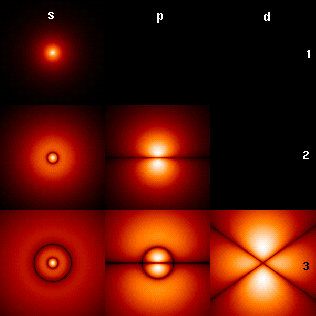
Рис. 7. Изображение плотности вероятности для электрона при различных квантовых числах

Заметим, что орбитали существуют независимо от того, находится на них электрон (занята ли орбиталь), или отсутствует (вакантные орбитали). Атом каждого элемента, начиная с водорода и заканчивая последним, полученным на сегодня элементом, имеет полный набор всех орбиталей на всех электронных уровнях. Однако их заполнение электронами происходит по мере увеличения порядкового номера, то есть, заряда ядра.

В атомах, имеющих несколько электронов в различных состояниях, их орбитали накладываются. Так, например, у атома углерода (рис.8) два электрона находится на s-орбитали (отмечены синим цветом в центральной части рисунка) и по одному электрону на двух р-орбиталях (отмечены красным и желтым цветом), третья орбиталь – р_z-вакантная.

Краткую запись распределения электронов в атоме по различным электронным оболочкам атома с учётом их главного и орбитального квантовых чисел n и l называют электронной конфигурацией атома. Электронная конфигурация — формула расположения электронов по различным электронным оболочкам атома химического элемента или молекулы.

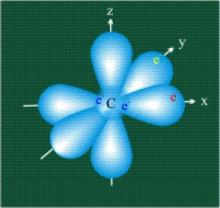
Рис. 8. Изображение орбиталей атома углерода

Любопытно отметить, что совсем недавно группе исследователей из Харьковского Физико – Технического Института с помощью эмиссионного электронного микроскопа (FEEM) впервые удалось «визуализировать» принципы квантовой механики и получить детальные изображения электронных орбиталей углерода (рис.8).

Рис. 8. Полученные в Харькове фотографии различного расположения электронных орбиталей в атоме углерода

3. Магнитное квантовое число характеризует ориентацию орбитали в пространстве и может принимать значения целых чисел от – до + , в том числе и значение 0 (m_l = -l … 0 … l).

Если исходить из классических представлений, то движущийся по замкнутой орбите электрон эквивалентен круговому току, магнитное поле которого взаимодействует с внешним магнитным полем. В предыдущей лабораторной работе вы получили расположение векторов магнитной индукции и силовые линии такого поля для витка с током. Электрон, как и всякий электрический заряд, движется по замкнутому контуру, имеет собственный магнитный момент. Плоскость электронной орбиты занимает определенное положение в пространстве, которое и характеризуется магнитным квантовым числом. Это положение можно характеризовать углом между направлением магнитного поля и осью перпендикулярной к плоскости орбиты.

Величина проекции этого момента на одну любую ось координат во внешнем магнитном поле принимает определенные квантовые значения, которые и характеризуют расположение подуровня в пространстве. Правильнее говорить, что орбитальное магнитное квантовое число m_l определяет значение составляющей проекции момента количества движения электрона на выделенное направление в пространстве .

Таким образом, магнитное квантовое число m_l характеризует расположение орбитали в пространстве. Его называют магнитным, так как оно определяет проекции орбитального магнитного момента электрона на ось атома. Магнитное квантовое число характеризует ориентацию электронных облаков по отношению к магнитной оси атома.

В отсутствии внешнего магнитного поля электроны на орбиталях с одинаковым значением квантового числа l энергетически равноценны (то есть их энергетические уровни, как говорят, вырождены). Однако в постоянном магнитном поле электрон может принимать различные дискретные уровни энергии. Это означает, что электроны становятся энергетически неравноценными. Например, р-состояния в магнитном поле принимают 3 значения вместо одного, d -состояния - 5 значений. Допустимые значения m_l для данного l: -l, ...-2,-1,0,+1,+2,...+l.

В литературе орбитали обозначают комбинацией квантовых чисел, выражающей пространственно - угловую зависимость вероятности нахождения электрона. При этом главное квантовое число обозначают цифрой, орбитальное квантовое число — соответствующей буквой и магнитное квантовое число — выражением в нижнем индексе, показывающем проекцию орбитали на декартовы оси x, y, z, например 2p_x, 3d_xy, 4f_z(x²-y²).

Тогда можно отметить следующее.

Для n = 1 возможно только одно значение орбитального квантового числа l = 0, поэтому оба электрона первого слоя будут s-электронами. Они находятся на s-орбитали шаровой симметрии. Водород имеет 1s1 – электрон, гелий – 2s2. Таким образом, в гелии первый электронный слой заполнен полностью и содержит два электрона.

При n = 2 l = 0, 1, то есть принимает два значения, и электронный слой распадается на два подуровня (табл. 3).

При l = 0 m = 0, и на этом подуровне могут быть только два электрона. Так, Li 1s22s1, Be 1s22s2 2s – это первый подуровень второго электронного слоя.

Второй подуровень, при котором l = 1 и m = -1, 0, +1, может содержать еще шесть электронов. Этот подуровень называется 2р-подуровнем, а соответствующие ему электроны называются 2р-электронами.

Таблица 3.

n	1	2	2	2	2	3	3
l	0	0	1	1	1	0	1
m	0	0	0	1	-1	0	1
Обозначение	1s	2s	2pZ	2pX	2pY	3s	3pZ

Кроме квантовых чисел n, l, m, известно еще одно. Это так называемый спин (S) электрона.

4. Спиновое квантовое число характеризует различие состояний двух электронов, принадлежащих одной орбитали, в зависимости от ориентировки их собственных моментов количеств движения. Число может иметь только два значения: . То есть, магнитное состояние квантуется, и существуют только два возможных состояния.

Известно, что магнитное поле возникает при движении электрического заряда по кривой траектории. Предполагая, что в электроне заряд каким-то образом вращается, говорят, что электрон имеет спин. Это предположение позволяет вычислить магнитное поле, создаваемое спином.

Упрощенно число показывает вращение электрона вокруг собственной оси. Поэтому первое число можно объяснить, в механическом приближении, достаточно просто: как будто бы в этом случае собственное вращение электрона (как шарика вокруг своей оси) соответствует одинаковому направлению движения по орбите (этого же шарика). Второе число соответствует противоположному направлению собственного и орбитального вращения.

Тонкие исследования показали, что электрон обладает не только электростатическим полем, но и магнитными свойствами. Если пропустить пучок электронов через сильно изменяющееся магнитное поле, то он распадается на два пучка. Степень отклонения свидетельствует о том, что каждый электрон ведет себя как маленький магнитик, который ориентирован по полю либо параллельно, либо в строго противоположном направлении (антипараллельно).

Спиновое состояние электрона наглядно можно представить и так, как будто с электроном связана «магнитная стрелка». В отсутствие магнитного поля способность ее к ориентации ни в чем себя не проявляет. Однако при наличии магнитного поля (рис. 10) она ориентируется двумя способами – либо по магнитному полю, либо против него, что и позволяет различать два спиновых состояния электрона.

Рис. 10. Объяснение спинового числа с привлечением аналогии магнитной стрелки

Заметим, что исторически спин потребовалось ввести для того, чтобы объяснить результаты тех экспериментов, которые указывали на наличие двух близких энергетических уровней, там, где можно было ожидать существование только одного. В 1925 г. Уленбек и Гаудсмит предложили, что электрон может вращаться вокруг своей собственной оси. Это объяснение, не является точным, но термин «спин» прижился и широко используется в теории.

Обратим внимание на то, что спин следует рассматривать как просто квантовое число, которое пришло из математически строгой теории. Понятие спина свойственно всем микрочастицам. Оно является столь же фундаментальным, как понятие массы и заряда. Спин следует воспринимать, как исходное, внутренне присущее всем микрочастицам качество, не связанное с каким либо «вращением» вокруг оси.

В одной орбитали может находиться не более двух электронов. При этом эти электроны имеют противоположные (антипараллельные) спины. Этот определяется принципом Паули. Принцип Паули дает возможность рассчитать емкость электронных уровней и подуровней. Повторим, сегодня принцип Паули и спин являются «вещами» чисто теоретическими (математическими), поэтому не следует искать в них особого «физического» смысла.

Порядок заполнения электронами орбиталей одного уровня (орбиталей с одинаковым значением главного квантового числа n) определяется правилом Клечковского, порядок заполнения электронами орбиталей в пределах одного подуровня (орбиталей с одинаковыми значениями главного квантового числа n и орбитального квантового числа l) определяется правилом Гунда (Хунда) (наибольшего суммарного спинового числа). Последовательность заполнения подуровней, найденная исходя из правила Клечковского, имеет вид:

К примеру, для атома бора порядок заполнения следующий

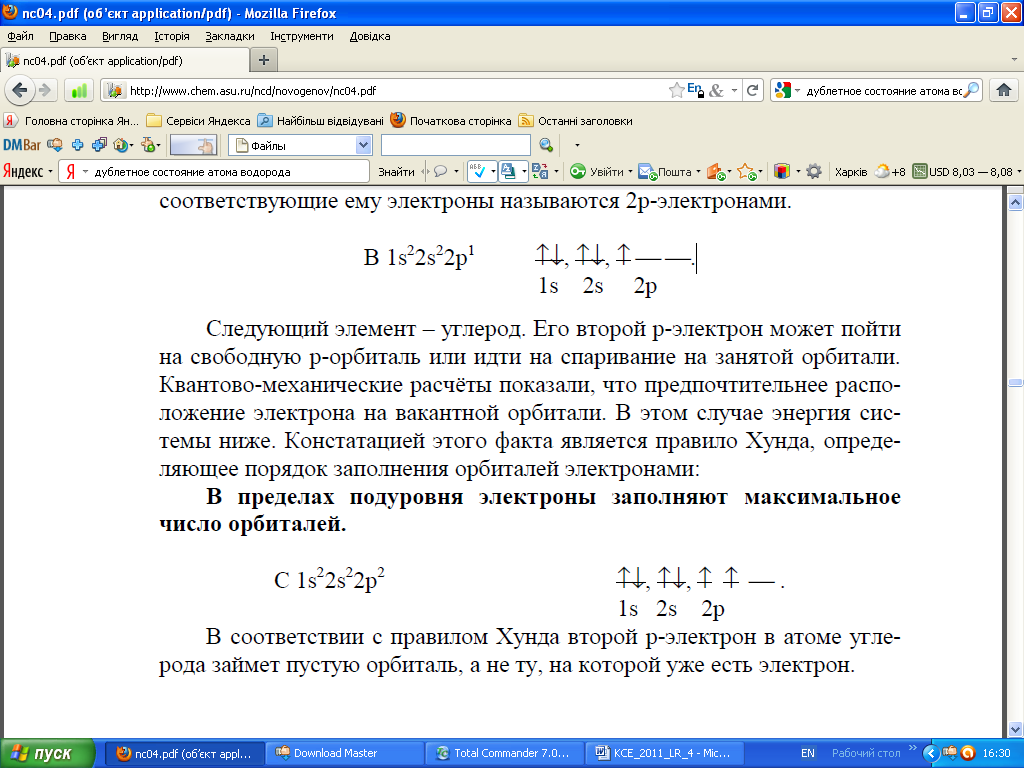
Стрелки, пересекающие линии, указывают спин электрона и его направление. Как несложно заметить, у атома бора на 1s уровне расположены два электрона с противоположными спинами. Аналогичное расположение имеет место для 2s уровня. На 2р имеется возможность для заполнения электронами трех подуровней, но заполнен всего один.

Следующий элемент углерод. Его второй р-электрон может пойти на свободную р-орбиталь или расположиться (с противоположным спином) на занятой уже электроном орбитали. Расчеты показали, что предпочтительнее расположение электрона на вакантной орбитали. В этом случае энергия системы ниже. Констатацией этого факта и является правило Гунда, определяющее порядок заполнения орбиталей. В пределах подуровня электроны заполняют максимальное число орбиталей. В соответствии с правилом Гунда второй р-электрон займет пустую орбиталь, а не ту, на которой есть электрон.

Порядок заполнения орбиталей электронами для других атомов представлен в таблице 4.

Таблица 4.

Название атома	Порядок заполнения электронами
Азот
Кислород
Фтор, неон

Итак, для полного описания состояния электрона в атоме используются следующие 4 параметра (рис.11).

В заключение еще раз подчеркнем следующее.

По современным представлениям понятия классической частицы и классической волны не способны передать всю специфику свойств микромира. Электроны и другие микрообъекты – это особые квантовые частицы или микрочастицы, в которых знакомые нам по макромиру корпускулярные и волновые свойства настолько «переплетены» и качественно изменены, что их следовало бы называть «волночастицами». Тем самым вместо двойственной качественно отличной природы форм материи (либо вещество либо поле) в микромире проявляется двуединая корпускулярно – волновая природа, общая для всех форм материи.

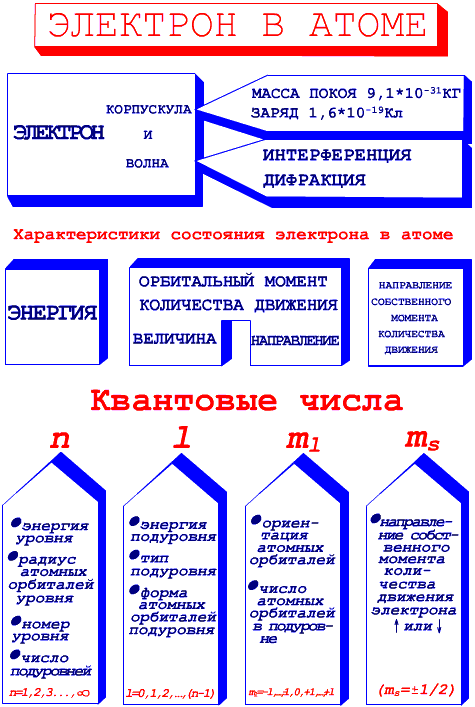
Рис. 11. Квантовые числа, используемые в квантовой механике для описания состояния электрона

Задание 1.

1. Кратко опишите, что представляет в современном понимании такая сущность, как электрон. Какую форму принимает его движение?

2. Кратко сформулируйте, как характеризуют в настоящее время состояние электрона.

Эксперимент 2. Изучение посредством моделирования основных понятий, связанных энергетическими состояниями атома

Задание 2.

1. Изучите, используя квантовомеханическую модель атома водорода, какой вид будет иметь график общей энергии электрона на данной орбитали в зависимости от главного квантового числа n .

Сделайте выводы о следующем.

1. Верно ли то, что энергия состояний электрона принимает дискретные значения и, если увеличивается, то электрон слабее связан с ядром, энергия такого электрона становится ближе к нулю, то есть к энергии свободного электрона, который покидает свой атом.

2. Какую надо сообщить внешнюю дополнительную энергию, чтобы электрон перешел в возбужденное состояние, характеризуемое главным квантовым числом .

3. Какие порции энергии будут излучены, если электрон будет возвращаться на основную орбиталь из возбужденного состояния с в первом случае единым переходом, а в другом случае - через промежуточный уровень с .