4. Линейные нормированные пространства Основные понятия и примеры

Наиболее важными для приложений являются метрические пространства, которые одновременно являются линейными пространствами. При этом расстояние должно сохраняться при сдвигах, т.е. должно выполняться равенство (x,y) = (x+z,y+z) для любых векторов. Дадим точное определение.

ОПРЕДЕЛЕНИЕ 15. Множество Х называется линейным нормированным пространством, если

1. X является линейным пространством,

2. На Х определена вещественнозначная функция ||х|| (норма), которая обладает следующими свойствами:

- ||х||  0, причем ||х|| = 0 только при х = 0,

- ||х|| = ||х||,

- ||х+y||  ||х||+||y||.

Наличие нормы позволяет ввести метрику на Х: (x,y) = ||хy||.

ПРЕДЛОЖЕНИЕ 10. Величина (x,y) обладает свойствами метрики.

ДОКАЗАТЕЛЬСТВО.

1. По определению нормы (x,y)  0, причем если (x,y) = ||хy||=0, то по определению нормы хy = 0, т.е. х = y.

2. (y,x) = ||y  х|| = ||(1)(х  y)|| = 1||х  y|| = ||х  y|| = (x,y).

3. (x,y) = ||х  y|| = ||(х  z)  (y  z)||  ||х  z|| + ||y  z|| =

= (x, z)+(z, y)

Все свойств расстояния (п. ) выполняются.

Очевидно, что так определенная метрика сохраняется при сдвигах, т.е. выполняется свойство (x,y) = (x+z,y+z). Следует иметь в виду, что не всякая метрика в линейном пространстве, обладающая этим свойством, порождается некоторой нормой. Так, на линейном пространстве можно определить дискретную метрику, расстояние сохраняется при сдвигах, но никакой нормой она не порождается.

Почти все примеры метрических пространств, рассмотренные в п. , в действительности являются линейными нормированными пространствами. Полные линейные нормированные пространства называются банаховыми.

1. Конечномерные пространства .

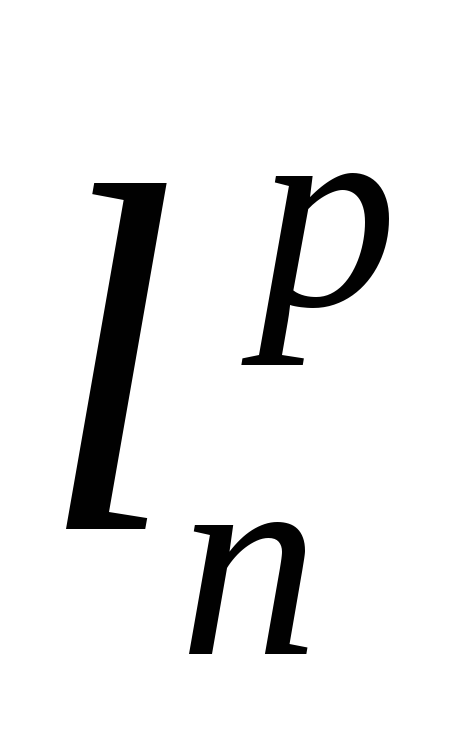Множество векторов является линейным пространством. Если определить норму вектора по формуле ||х||_р=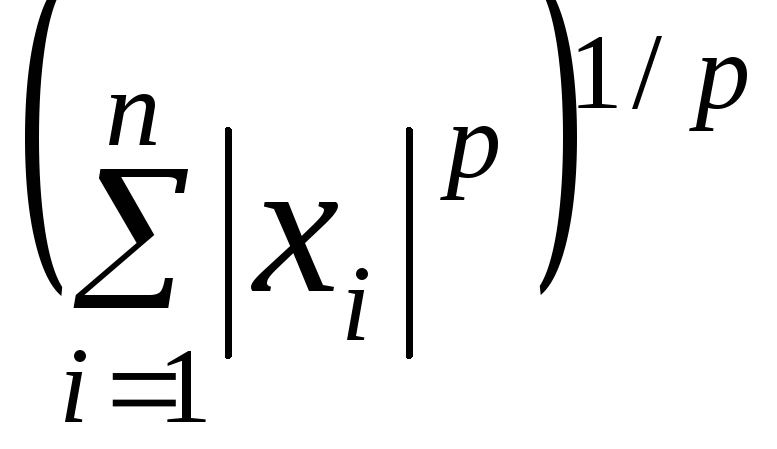(свойства нормы можно проверить с использованием неравенств Гельдера и Минковского), то расстояние, введенное в п. , порождается этой нормой. Аналогично для случаяр=: соответствующая норма имеет вид ||х||_=maxx_i. Все эти пространства полные, т.е. банаховы.

2. Пространство С.

Множество непрерывных функций на отрезке [0,1] является линейным пространством, поскольку функции можно складывать и умножать на скаляры (поточечно) c сохранением непрерывности и при этом справедливы аксиомы 1-8 из п. 1. Если ввести норму по формуле ||х  y|| = max(х(t)), где максимум берется по всем значениям t, то метрика, порождаемая этой нормой, совпадает с метрикой из п. . Тем самым, пространство С является линейным нормированным пространством. Поскольку это пространство полное, оно банахово.

3. Пространство m.

Сумма ограниченных последовательностей  ограниченная последовательность, ограниченность сохраняется и при умножении последовательности на число. Аксиомы линейного пространства легко проверяются. Тем самым, множество ограниченных последовательностей является линейным пространством. Если определить норму вектора ||х  y|| = max(х_i) (свойства нормы необходимо проверить!), то метрика в пространстве m (п.) порождается этой нормой. Пространство является банаховым.

Естественно, так же определяется норма и в пространстве сходящихся последовательностей с подпространстве m.

4. Пространство L^p_с.

Здесь норма, порождающая метрику из п. , задается формулой ||х  y||_p=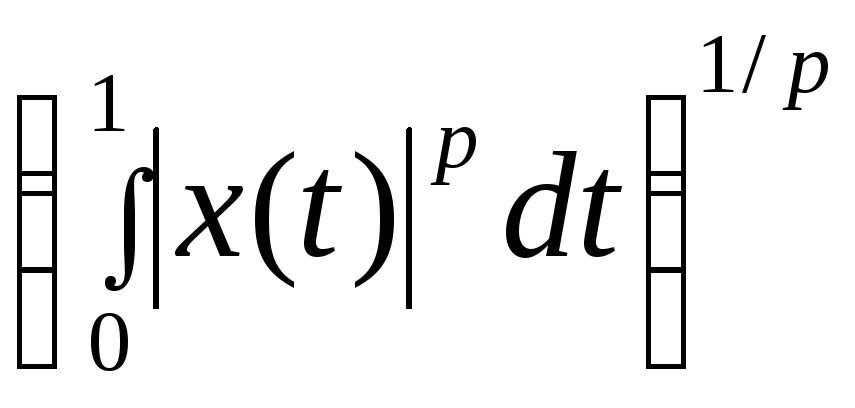. Пространство банаховым не является.

5. Пространство l^p.

Это пространство является линейным. Для этого сначала надо проверить, что сумма последовательностей из l^p также является элементом l^p. Норма в l^p определяется формулой ||х||=. Свойства нормы также необходимо проверить. Пространствоl^p банахово.

Проверим, что линейные операции и норма как функция на линейном нормированном пространстве непрерывны.

ПРЕДЛОЖЕНИЕ 11. Если х_nх, y_ny в пространстве Х и _n в пространстве R, то

1. х_n+y_nх+y;

2. _nх_nх;

3. ||х_n||  ||х||.

ДОКАЗАТЕЛЬСТВО.

1. ||(х_n + y_n)  (х + y) || = ||(х_n  х) + (y_n  y) || 

 ||х_n  х|| + ||y_n  y||.

Правая часть стремится к 0 при возрастании n, а тогда по теореме о милиционерах

||(х_n+y_n)  (х+y)||0, т.е. х_n+y_nх+y.

2. ||_nх_n  х|| = ||_n(х_n  х) + х(_n  )||  _n||х_n  х|| +

+_n||х||.

Здесь также правая часть стремится к 0 при возрастании n, при этом используется ограниченность сходящейся последовательности {_n}. Таким образом, ||_nх_n  х||0, т.е. _nх_nх.

3. Из неравенства треугольника для нормы следует обратное неравенство треугольника (||х_n||  ||х||)  ||х_n  х||. Отсюда и следует, что ||х_n|| ||х||.

Ограниченность множества в нашем случае согласно замечанию п. равносильна тому, что множество содержится в некотором шаре с центром 0, т.е. ограниченности норм элементов множества. Шары в линейных нормированных пространствах обладают некоторыми дополнительными свойствами по сравнению с общими метрическими пространствами.

ПРЕДЛОЖЕНИЕ 12. Шары (замкнутые шары) в линейном нормированном пространстве являются выпуклыми множествами.

ДОКАЗАТЕЛЬСТВО. Рассмотрим шар B(a,r) (для замкнутых шаров рассуждение аналогичное). Пусть x,yB(a,r) и числа ,  удовлетворяют условиям ,  0, + = 1. Если мы докажем, что x +y B(a,r), то выпуклость шара будет доказана (п. 1). Имеем ||x + y  a|| = ||(x  a) + (y  a)||  ||(x  a)|| + ||(y  a)|| = = ||х  a|| + ||y a|| < r+r=r, что и требовалось.

ПРЕДЛОЖЕНИЕ 13. Замыканием шара B(a,r) (r>0) является замкнутый шар (a,r). Заметим, что в общем случае метрических пространств это неверно (см. п. ).

ДОКАЗАТЕЛЬСТВО. 1. Пусть y – предельная точка шара B(a,r), т.е. при любом n существует точка х_nB(a,r) такая, что ||yх_n|| < 1/n. Отсюда получим: ||y  a||  ||y  х_n|| + ||х_n  a|| < r+1/n. В силу произвольности n справедливо неравенство ||y  a||  r, т.е. y(a,r). Тем самым доказано, что замыкание шара B(a ,r) содержится в шаре (a,r). Эта часть доказательства справедлива в любых метрических пространствах.

2. Пусть теперь y(a,r)\B(a,r). Это означает, что ||y  a|| = r. Надо доказать, что точка y  предельная для шара B(a,r). Для этого рассмотрим точки х_n = . Очевидно, что||х_na|| = <r, т.е. х_nB(a,r). По предложению 11, х_ny, т.е. любая точка шара (a,r) содержится в замыкании шара B(a, r).

Важным является понятие подпространства линейного нормированного пространства.

ОПРЕДЕЛЕНИЕ 16. Замкнутое линейное многообразие в линейном нормированном пространстве называется линейным подпространством.

Позднее будет установлено, что конечномерные многообразия непременно являются подпространствами.

Например, в пространстве l¹ подпространством является множество S={xl¹:}. Очевидно, что это множество является линейным многообразием. Проверим замкнутостьS. Из сходимости ряда следует сходимость ряда(курс математического анализа), т.е. функцияf(x) = определена на всем пространствеl¹. Проверьте самостоятельно ее непрерывность на пространстве l¹ (см. задачу 3.14). Но прообраз S замкнутого множества {0} при непрерывном отображении является замкнутым.

Рассмотрим линейное многообразие в пространстве С, состоящее из непрерывно дифференцируемых функций. Линейность этого многообразия следует из правил дифференцирования. Многообразие не является подпространством, поскольку по теореме Вейерштрасса любую непрерывную функцию можно сколь угодно точно приблизить многочленом (это равносильно малости расстояния в метрике С), т.е. замыкание многообразия совпадает со всем пространством С. При этом в С существуют недифференцируемые функции (например, х1/2 ).

В общих линейных нормированных пространствах не определено понятие угла между векторами. Тем не менее, можно определить вектор, «почти ортогональный» подпространству.

ТЕОРЕМА 6 (Ф.Рисс). Пусть L подпространство линейного нормированного пространства Х, не совпадающее со всем пространством. Для любого >0 существует вектор y такой, что 1 для всех хL.

ДОКАЗАТЕЛЬСТВО. Пусть y₀L, d = . Прежде всего,d > 0. Действительно, если d = 0, то y₀  предельная точка L, т.е. в силу замкнутости L должно выполняться условие y₀L, что противоречит выбору y₀. По определению точной нижней грани существует элемент х₀ L такой, что d  <d/(1). Положим . Выполняется условиеyL, поскольку в противном случае мы бы имели y₀ = х₀+yL. Далее,

.

Пусть хL. Имеем

.

Поскольку L, то по определению числа d имеем . По определению элементах₀ справедливо неравенство <d/(1). Отсюда = 1, что и требовалось.

Читателю предлагается проиллюстрировать эту теорему (и доказательство) графически, после чего станет понятно, почему полученный вектор при малых значениях  естественно назвать почти ортогональным подпространству.

Следует иметь в виду, что вектор со свойством может и не существовать. В важном частном случае гильбертова пространства (п. ) такой вектор существует.