Компактность в линейных нормированных пространствах

О компактных множествах в линейных нормированных пространствах можно сказать больше, чем для общих метрических пространств. В п. доказано, что в пространствах любое замкнутое ограниченное множество является компактным. Пространства, для которых это так, называютсялокально компактными. Справедлива следующая важная теорема.

ТЕОРЕМА 8. Для того чтобы линейное нормированное пространство являлось локально компактным, необходима и достаточна его конечномерность.

ДОКАЗАТЕЛЬСТВО. 1. Достаточность. По теореме 6, п-мерное линейное нормированное пространство Х изоморфно пространству . Последнее (п. ) является локально компактным. ПустьА: Хизоморфизм, M замкнутое ограниченное подмножество Х. Множество А(M) замкнутое, поскольку замкнутым является его прообраз M при непрерывном отображении А^1 (п.) и ограниченным (п. ). Таким образом, множество А(M)  компактное (п. ). Но тогда компактным является и его образM при непрерывном отображении А^1 (п. ), что и требовалось.

2. Необходимость. Пусть в линейном нормированном пространстве Х любое замкнутое ограниченное множество является компактным.

Если пространство состоит только из вектора 0 (это ничему не противоречит), то оно 0-мерное, т. е. конечномерное.

Пусть это не так и вектор у₁Х удовлетворяет условию ||у₁|| = 1. Обозначим через L₁ линейную оболочку вектора у₁, т.е. множество векторов {₁у₁: ₁R}. Если Х = L₁, то пространство Х конечномерное (одномерное).

В противном случае L₁ как конечномерное линейное многообразие является подпространством Х (п.). По теореме Рисса (п.) при  = 0.5 в этом случае существует вектор у₂ такой, что ||у₂|| = 1, ||у₂  х||  0.5 при хL₁.Обозначим через L₂ линейную оболочку векторов у₁ и у₂, т.е. множество векторов {₁у₁ + ₂у₂: ₁, ₂R}. Если Х = L₂, то пространство Х конечномерное (двухмерное).

В противном случае L₂ как конечномерное линейное многообразие является подпространством Х (п.). По теореме Рисса (п.) при  = 0.5 в этом случае существует вектор у₃ такой, что ||у₃|| = 1, ||у₃  х||  0.5 при хL₂. Обозначим через L₃ линейную оболочку векторов у₁, у₂ и у₃, т.е. множество векторов {₁у₁ + ₂у₂ + ₃у₃: ₁, ₂, ₃R}. Если Х = L₃, то пространство Х конечномерное (трехмерное).

Продолжая этот процесс, придем к одной из двух ситуаций: либо при некотором п выполняется равенство Х=L_n, либо получим последовательность у₁, у₂,…, у_n,… со свойствами ||у_i|| = 1 и ||у_iу_j||  0.5 при ij. Очевидно, что эта последовательность ограниченная и замкнутая, но при этом не компактная (из нее нельзя извлечь сходящуюся подпоследовательность). Противоречие завершает доказательство.

Важную роль в функциональном анализе играют критерии компактности множеств в различных линейных нормированных пространствах. Приведем без доказательств два таких результата. Напомним (п. ), что компактное множество всегда замкнутое и ограниченное. В конечномерных пространствах этого и достаточно. Фактически в следующих двух теоремах устанавливается, что надо добавить к замкнутости и ограниченности в некоторых бесконечномерных пространствах, чтобы обеспечить компактность множеств.

1. Пространство С.

Напомним известное из математического анализа определение равномерной непрерывности функции. Функция х(t), определенная на числовом множестве U, называется равномерно непрерывной, если >0 >0 t₁, t₂U t₁t₂<  x(t₁) x(t₂) < . Смысл этого условия в том, что для данного  годится одно и то же значение  для всех точек множества. В курсе математического анализа установлено, что непрерывная функция, заданная на отрезке [a,b], является равномерно непрерывной. Если для всех функций из множества М  С для заданного  > 0 годится одно и то же число  > 0, то множество М называется равностепенно равномерно непрерывным. Более формально множество функций М  С называется равностепенно равномерно непрерывным, если >0 >0 xМ t₁, t₂[0,1] t₁t₂ <   x(t₁) x(t₂)<.

ТЕОРЕМА 9 (Арцела). Для того, чтобы замкнутое ограниченное подмножество пространства С было компактным, необходимо и достаточно, чтобы подмножество было равностепенно равномерно непрерывным.

2. Пространства l^р.

ТЕОРЕМА 10. Для того, чтобы замкнутое ограниченное подмножество М пространства l^р было компактным, необходимо и достаточно, чтобы

>0 N xМ .
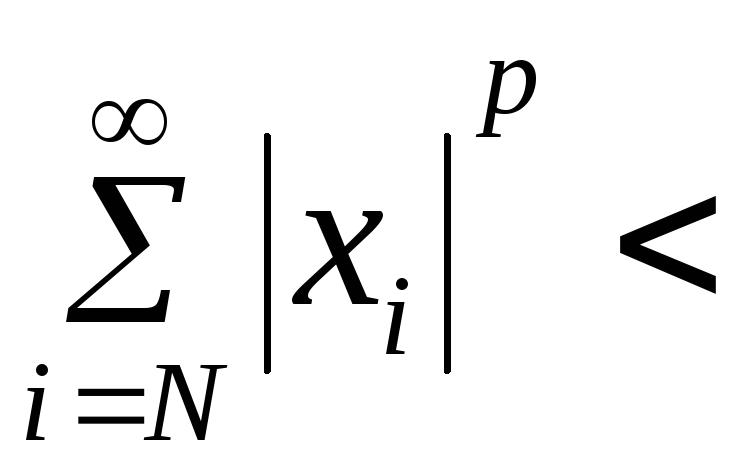