2. Некоторые важные неравенства

1. Пусть p, q – положительные вещественные числа, такие, что 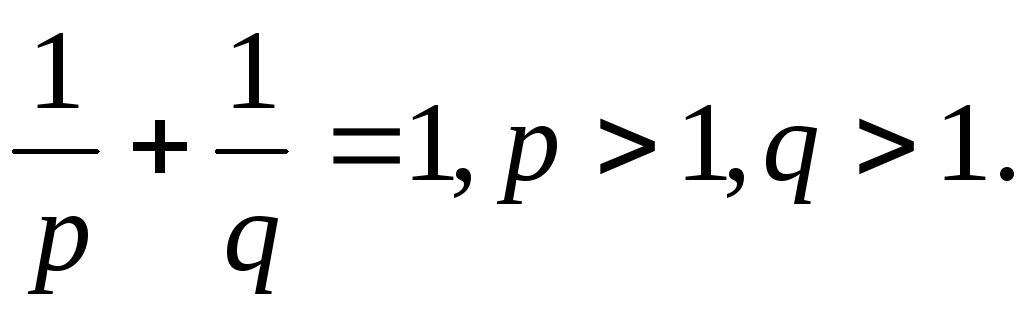Тогда при любыха, b выполняется неравенство

.

ДОКАЗАТЕЛЬСТВО. Поскольку в неравенстве фигурируют только модули, можно считать, что числа а, b положительные. Рассмотрим функцию (t) = t^mmt при t>0, m(0,1). Имеем

(t) = mt^m1m =m(t^m11).

Отсюда, функция (t) принимает наибольшее значение при t=1, т.е. t^mmt 1m или t^m1  m(t1). Положив t = a^p/b^q, m=1/p (из условия следует, что p > 1), получаем ab^q/p1  (1/p)(a^pb^q1). Умножая это неравенство на b^q, получаем ab^qq/pb^q  (1/p) (a^p  b^q). Из условия qq/p = 1. Отсюда, ab  , что и требовалось.

2. Неравенство Гельдера для конечных сумм.

Пусть x₁,x₂,…,x_n; y₁,y₂,…,y_n  вещественные числа. Тогда

.

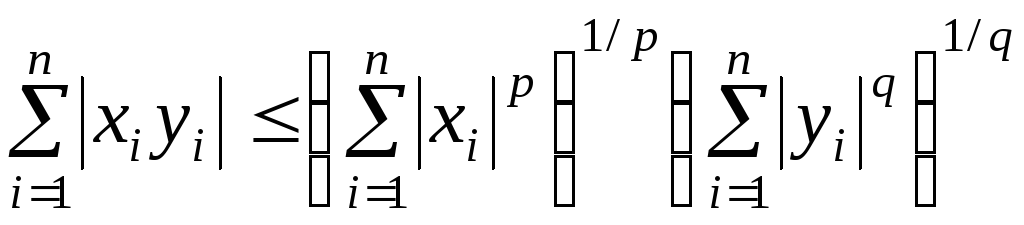
ДОКАЗАТЕЛЬСТВО. Пусть .Можно считать, что A>0, B>0 – в противном случае x₁=…=x_n=0 или y₁ =…= y_n = 0 и неравенство очевидно. Полагая a = x_i/A, b = y_i/B в неравенстве п. 1, получим . Суммируя, получим,

что равносильно нужному неравенству.

При p = q = 2 неравенство Гельдера превращается в известное из линейной алгебры неравенство Коши-Буняковского

.

В п. доказывается более общая форма этого неравенства.

3. Неравенство Гельдера для рядов.

Пусть ряды сходятся. Тогда сходится и ряд, причем

.

Это неравенство получается из предыдущего с помощью предельного перехода.

4. Интегральное неравенство Гельдера.

Пусть х(t), y(t) – функции, непрерывные на отрезке [0,1], . Тогда

.

ДОКАЗАТЕЛЬСТВО следует схеме из п. 2. Пусть . Как и раньше, можно считать, чтоA > 0, B > 0 – в противном случае хотя бы одна из функций нулевая и неравенство очевидно. В неравенство п. 1 подставим а = х(t)/A, b = y(t)/A. Получаем:

.

Интегрируя это неравенство от 0 до 1, получим:

,

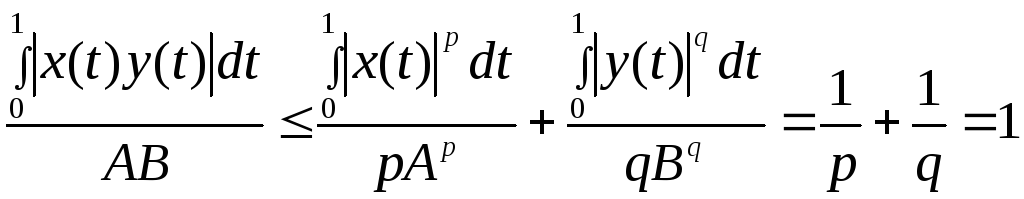что равносильно нужному неравенству.

5. Неравенство Минковского для конечных сумм.

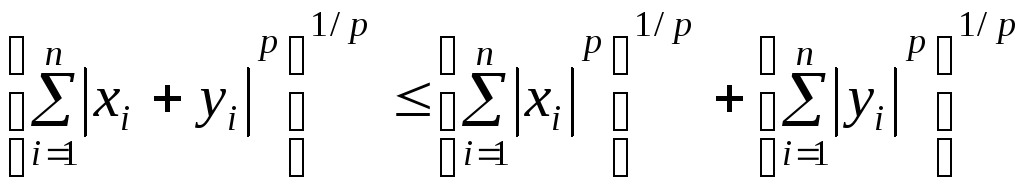
при p > 1.

ДОКАЗАТЕЛЬСТВО. Запишем очевидное неравенство

.

К слагаемым в правой части применим неравенство Гельдера для конечных сумм (п.2):

Из равенства следуетq(p1) = p. Подставляя, получим

.

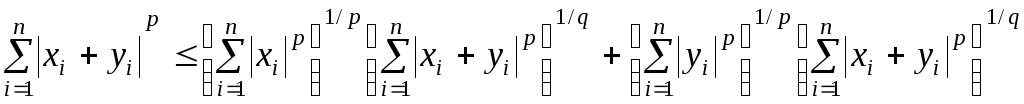Поделив обе части неравенства на 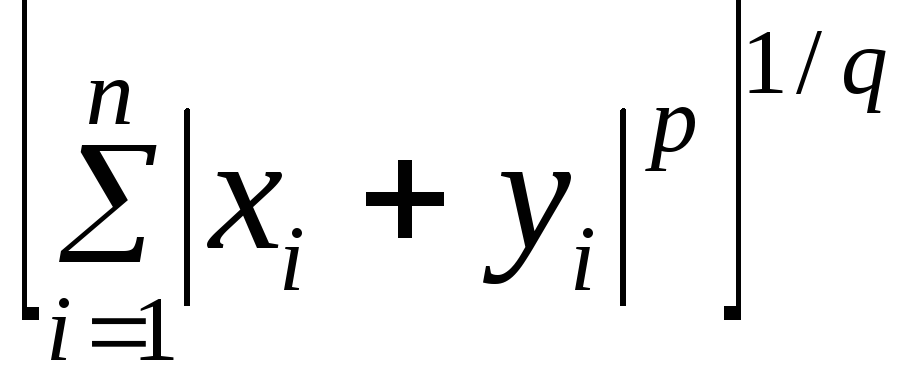, получим нужное неравенство.

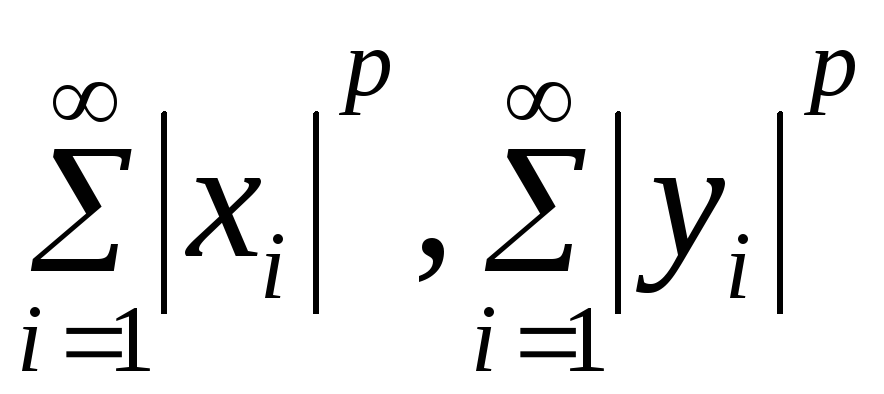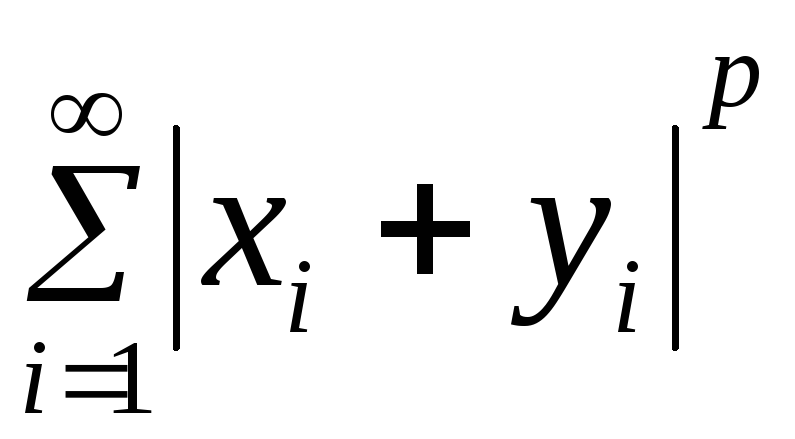6. Неравенство Минковского для рядов. Пусть p>1. Если сходятся ряды , то сходится ряд, причем

.

Это неравенство получается предельным переходом из предыдущего.

7. Неравенство Минковского для интегралов. Пусть х(t), y(t) – функции, непрерывные на отрезке [0,1], p>1. Тогда

.

Доказательство легко получить из неравенства Гельдера для интеграла аналогично п. 5.

3. Метрические пространства Определение и простейшие свойства

Идея метрического пространства формализует понятие расстояния, к которому мы все привыкли. В обобщенном смысле можно ввести расстояние между весьма сложными объектами, например, функциями или последовательностями. Оказывается, существенными являются три свойства расстояния.

ОПРЕДЕЛЕНИЕ 1. Метрическим пространством называется множество Х, любым двум элементам (точкам) х,у которого сопоставлено число (х,у), удовлетворяющее следующим условиям:

1) Неотрицательность: (х,у)  0, причем условие (х,у) = 0 равносильно тому, что х = у. Это означает, что расстояние между различными точками положительное.

2) Симметричность: (х,у) = (у,х).

3) Неравенство треугольника: (х,у)  (х,z)+(z,у). Это неравенство обобщает известное правило: сумма длин двух сторон треугольника не меньше третьей.

Функция  называется метрикой или расстоянием.

Из неравенства треугольника вытекает полезное обратное неравенство треугольника:  (х,z)(z,у)  (х,у), которое для плоских треугольников известно из школьного курса геометрии. Действительно, по неравенству треугольника и симметрии метрики (х,z)  (х,у) + (z,у), (z,у)  (х,у) + (х,z). Из первого неравенства следует (х,z)  (z,у)  (х,у), из второго – (z,у) (х,z)  (х,у). Нужное неравенство следует из того, что пара неравенств а  b, а  b равносильна одному неравенству а  b.

Любое множество Y  X можно считать наделенным метрикой . Оно называется подпространством X.