Е.М.БРОНШТЕЙН

ОСНОВЫ ФУНКЦИОНАЛЬНОГО АНАЛИЗА

Уфа-2004

Министерство образования Российской Федерации

Уфимский государственный авиационный технический университет

Е.М.БРОНШТЕЙН

Основы функционального анализа

Учебное пособие

Уфа-2004

УДК 517.98(07)

ББК 22.162(97)

Б 88

Б 88 Бронштейн Е.М. Основы функционального анализа. Учебное пособие.-Уфа: УГАТУ, 2004.- 62 с.

Пособие подготовлено в соответствии с программой курса «Функциональный анализ» для студентов специальности 351500 «Математическое обеспечение и администрирование информационных систем», обучающихся по очно-заочной (вечерней) форме. Включает лекционный материал, упражнения для практических занятий, темы рефератов и вопросы зачета.

Библиогр: 4 назв.

Печатается по решению редакционно-издательского совета УГАТУ

Научный редактор – канд. физ.-мат. наук, доц. Водопьянов В.В.

Рецензенты: кафедра математического анализа Башкирского государственного педагогического университета, зав. кафедрой доктор физ.-мат. наук, проф. Гадыльшин Р.Р.; чл.-корр. АН РБ, доктор физ.-мат. наук, проф. Юлмухаметов Р.С.

 Е.М.Бронштейн, 2004

 Уфимский государственный авиационный

технический университет, 2004

ОГЛАВЛЕНИЕ

Предисловие 4

1. Введение. Предварительные сведения 5

2. Некоторые важные неравенства 7

3. Метрические пространства 11

Определение и простейшие свойства 11

Последовательности и их пределы. 11

Примеры метрических пространств 14

Замыкания множеств. Замкнутые и открытые множества 18

Непрерывные отображения 21

Полные метрические пространства 23

Компактные метрические пространства 27

4. Линейные нормированные пространства 31

Основные понятия и примеры 31

Изоморфные и изометричные линейные нормированные пространства 36

Компактность в линейных нормированных пространствах 40

Гильбертовы пространства 43

5. Линейные операторы 49

Пространство линейных операторов 49

Сопряженные пространства и слабая сходимость 53

Три фундаментальные теоремы функционального анализа 56

6. Литература 59

7. Темы рефератов 60

8. Вопросы зачета 61

9. Указатель терминов и результатов 62

Предисловие

Курс функционального анализа завершающий в математическом цикле специальности 351500 «Математическое обеспечение и администрирование информационных систем». Его цель – обобщить и интегрировать знания, полученные при изучении ряда предшествующих дисциплин. Высокий уровень абстракции вызывает серьезные затруднения при изучении, особенно у студентов, обучающихся по очно-заочной форме. Следует отметить, что краткого изложения основных понятий функционального анализа в объеме, необходимом для указанной специальности, не существует. Хорошие учебные пособия являются весьма объемными и не всегда доступными. Эти обстоятельства потребовали создания настоящего пособия. В нем содержится изложение как лекционного материала, так и упражнений в объеме, превышающем потребности практических занятий. После изучения дисциплины студенты должны подготовить рефераты, тематика которых также приводится в пособии.

Следует отметить, что результаты разбиты на две группы. Наиболее принципиальные с точки зрения автора именуются теоремами, остальные – предложениями.

Автор благодарен научному редактору В.В.Водопьянову, тщательная работа которого содействовала существенному улучшению текста пособия.

1. Введение. Предварительные сведения

Функциональный анализ изучает общие свойства пространств и их отображений. Что именно понимается под пространством, будет уточняться по мере изложения. Особое внимание в функциональном анализе уделяется пространствам, элементами которых являются функции и последовательности. Столь общий взгляд на вещи позволяет увидеть много общего в весьма далеких предметах. Функциональный анализ опирается на курсы математического анализа, алгебры и теории чисел, геометрии и топологии.

Напомним некоторые важные для дальнейшего понятия.

1. Функцией или отображением f: XY называется правило, которое каждому элементу множества X сопоставляет элемент множества Y. Элемент из Y, сопоставленный элементу хX, обозначается через f (х). Если X₁  X, то образом X₁ при отображении f называется множество f(X₁) = {f(x): xX₁}  Y. Если Y₁  Y, то прообразом Y₁ при отображении f называется множество f ^1(Y₁) = {x: f(x) Y₁}  X. Тождественное отображение i_Х: XХ имеет вид i(x) = x для любого xX. Отображение f:XY называется взаимно однозначным или биективным (биекцией), если f(X) = Y и из того, что f(х₁) = f(х₂) следует равенство х₁ = х₂.

2. Суперпозицией отображений f:XY, g: YZ, называется отображение fg:XZ, действующее по правилу fg(х) = g(f(х)). Суперпозиция взаимно однозначных отображений является взаимно однозначным отображением. Отображение f ^1:Y X называется обратным к f, если ff ^1 = i_X, f ^1f = i_Y. Обозначения прообраза множества и обратной функции совпадают, но смысл их различен. В первом случае он применяется к множеству и значением является множество, во втором – к элементу и значением является элемент. Прообраз множества существует всегда, а обратная функция не всегда. Например, функция х² определенная на всей числовой прямой R, не имеет обратной. Та же функция, рассматриваемая на множестве [0,), имеет обратную, ею является функция .

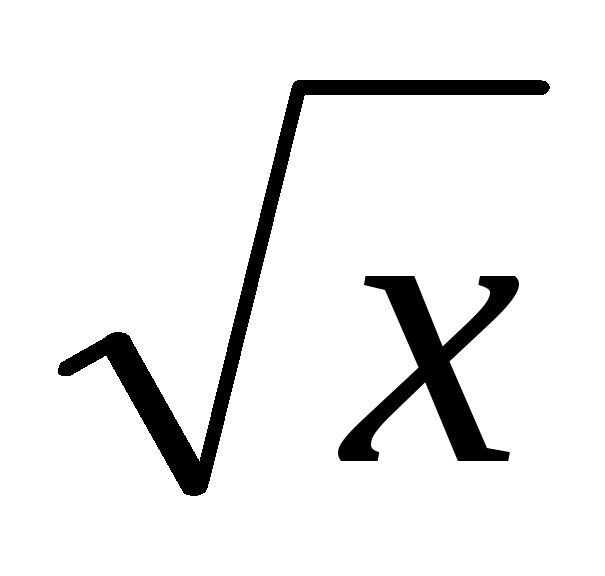Необходимым и достаточным условием существования отображения f ^1 является биективность отображения f. Справедлива следующая формула: (fg)^1= g^1f^1.

3. Числовое множество А называется ограниченным сверху, если существует такое число М, что все числа из А не превосходят М. Число М называется верхней гранью А. Множество ограниченное сверху имеет бесконечно много верхних граней, поскольку любое число, большее верхней грани, само является верхней гранью. Наименьшая из верхних граней называется точной верхней гранью и обозначается sup А (читается супремум А). Аналогично определяются множество ограниченное снизу, нижняя грань, точная нижняя грань как наибольшая из нижних граней, она обозначается inf А (читается инфимум А). Основная теорема теории вещественных чисел утверждает, что ограниченное сверху множество вещественных чисел имеет точную верхнюю грань, ограниченное снизу – точную нижнюю грань. Следует иметь в виду, что для множества, состоящего только из рациональных чисел, это неверно. Грани ограниченного множества могут принадлежать или не принадлежать множеству. Так, оба множества (0,1), [0,1] имеют точные верхние грани 1 и нижние 0. В первом случае они не входят во множество, во втором – входят. Если supАА, то говорят, что множество А имеет максимум (в этом случае вместо supА используют обозначение max А). Аналогично определяется минимум множества min А.

4. Линейным (или векторным) пространством называется множество X, для которого определены операции сложения x+y и умножения векторов на числа x, обладающие следующими свойствами:

1. x+y = y+x;

2. (x+y)+z = y+(x+z);

3. Существует такой элемент (нулевой) 0  X, что x+0 = x для любого x;

4. Для всякого xX существует обратный (x), т.е. такой, что x+(x) = 0;

5. ()x = (x);

6. (+)x = x+x;

7. (x+y) = x+y

8. 1x = x.

Вектора x₁, x₂,…, x_n называются линейно независимыми, если из равенства ₁x₁+₂x₂+…+_nx_n = 0 следует, что ₁ = ₂ = … = _n = 0. В противном случае вектора называются линейно зависимыми. Линейное пространство называется п-мерным, если в нем существует п и не существует большего числа линейно независимых векторов.

Любой набор из п линейно независимых векторов в n-мерном пространстве называется базисом линейного пространства. Всякий вектор п-мерного пространства представим единственным образом в виде линейной комбинации ₁x₁+₂x₂+…+_nx_n векторов базиса {x₁,…, x_n}. Если в линейном пространстве существует сколь угодно много линейно независимых векторов, то пространство называется бесконечномерным. Важными для дальнейшего примерами бесконечномерных линейных пространств являются пространство функций, непрерывных на отрезке [0,1] и пространство последовательностей.

5. Множество векторов в X, замкнутое относительно операций сложения и умножения на числа, называется линейным многообразием. Множество векторов М, которое вместе с любыми двумя точками содержит прямую, через них проходящую (здесь определение прямой мы не даем), называется аффинным многообразием. Если x и y – две точки из М, то любая точка прямой, проходящей через x и y представима в виде x +y при некоторых числах ,  таких, что +=1. Аффинное многообразие, содержащее нулевой вектор, является линейным многообразием. Линейное многообразие всегда является аффинным многообразием.

6. Множество М в линейном пространстве называется выпуклым, если вместе с любыми двумя точками оно содержит соединяющий их отрезок. Если x и y – две точки из М, то любая точка отрезка, соединяющего x и y представима в виде x +y при некоторых числах ,  таких, что ,0, +=1. Отрезок с концами x и y обозначается [x,y]. Отсюда следует, что аффинное (а значит и линейное) многообразие является выпуклым.