Примеры метрических пространств

1. Множество вещественных чисел R.

Этот пример, разумеется, хорошо известен. Расстояние определяется по правилу (х,у) =ху. 1 и 2 свойства расстояния очевидны, неравенство треугольника следует из известного неравенства а+b a+b при заменах a: = хz, b: = zy. Сходимость, естественно, совпадает с известным понятием сходимости числовой последовательности.

2. Конечномерные метрические пространства .

Рассмотрим множество векторов вида х = (х₁,х₂,…, х_n) c вещественными компонентами. Расстояние можно определять по разному. Пусть число р1. Определим величину _p(х,у) = . 1 и 2 свойства метрики очевидны, неравенство треугольника следует из неравенства Минковского (п. 2). Множество n – мерных векторов с расстоянием _p(х,у) является метрическим пространством, которое обозначается . Рассмотрим вопрос о сходимости в этих пространствах. Еслих^(k)х⁽⁰⁾, то

.

Но тогда и при k. Поскольку

,

то из неотрицательности модуля следует, что  0. А это означает, что . Обратно еслидля всехi, то по теореме о сумме сходящихся последовательностей получим , откуда х^(k)х⁽⁰⁾ в пространстве . Таким образом, сходимость в пространствахравносильна покоординатной сходимости.

На множестве n-мерных векторов можно определить еще одно расстояние: _(х,у) = . Свойства метрики легко проверяются, впрочем, сходные рассуждения будут приведены в дальнейшем. Здесь сходимость также равносильна покоординатной. Проверьте это самостоятельно.

Особый случай – р = 2. В курсе линейной алгебры пространство называется эвклидовым, мы пока никак не пользуемся тем, что вектора можно складывать и умножать на числа.

Рассмотрим замкнутые шары пространств при различных значенияхр с центром в точке 0 = (0,0) и радиусом 1. Это есть множества вида {(x₁,x₂): x₁^p+x₂^p  1}. Все круги содержат точки (1,0), (0,1). При р =2 это есть обычный евклидов круг, при р < 2 шар является подмножеством круга, при р = 1 шар является квадратом, диагонали которого расположены на координатных осях. При р > 2 шар объемлет обычный круг, при р =  получим квадрат, стороны которого параллельны осям координат.

3. Пространство непрерывных функций С.

Рассмотрим множество непрерывных функций, определенных на отрезке [0,1]. Тем самым, здесь точкой является функция. Определим расстояние (свойства предстоит проверить!) следующим образом: (х,у) =. Поскольку функциянепрерывна на отрезке [0,1], то по теореме Вейерштрасса (см. математический анализ!) она достигает максимального значения, так что определение корректно.

Проверим свойства расстояния.

1) Очевидно, что (х,у)  0. Пусть (х,у) = 0. Это означает, что = 0 при любом t [0,1], т.е функции совпадают (х = у).

2) Симметричность следует из того, что , а тогда равны и максимумы этих функций.

3) Для доказательства неравенства треугольника запишем неравенство, справедливое в любой точке отрезка: . Отсюда, по определению как максимального значения получаем неравенство  (х,z) + (z,y). поскольку это неравенство справедливо при всех значениях аргумента, то (х,у)  (х,z) + (z,y), что и требовалось. Это метрическое пространство обозначается С[0,1]. Опишем сходимость в этом пространстве. Если х_nx₀ в пространстве С[0,1], то , т.е.

>0 N n>N t[0,1] . В математическом анализе такая сходимость функций назывался равномерной в отличие от поточечной, которая состоит в том, чтох_n(t)x₀(t) при любом t[0,1], т.е. в формальном виде

t[0,1] >0 N n> N .

3. Пространство ограниченных последовательностей т.

Рассмотрим множество последовательностей х=(х₁,х₂,…,х_n,…), каждая из которых ограничена, т.е х_n М(х) (этим подчеркнуто, что для каждой последовательности границы свои). Например, последовательность (1000, 1, 1000, 1, 1000, 1, 1000,…) входит в т, а последовательность (1, 1, 2, 1, 3, 1, 4,…) нет. Определим расстояние (свойства расстояния проверьте сами – это делается так же, как и в предыдущем примере): (х,у)=Из ограниченности последовательностейх,у следует, что ограничена и последовательность , т.е. по теореме о точной верхней грани введенное расстояние всегда определено. При этом максимальное значение может не достигаться. Например, пустьу=(0,0,…,0,…); х=(0, 1/2, 3/4,…,(n1)/n,…). Проверьте, что не существует и докажите, что(х,у)=1.

Пусть х^(k)х⁽⁰⁾ в пространстве т. Поскольку при любом i =(х^(k) ,х⁽⁰⁾)0, то в силу неотрицательности по теореме о милиционерах 0, т.е. из сходимости в пространстве т следует покомпонентная сходимость. Обратное неверно: из покомпонентной сходимости не следует сходимость в пространстве т. В качестве примера рассмотрим последовательности х^(k), где все компоненты кроме k-ой нулевые, а . Очевидно, что0 при любом i (в соответствующей последовательности все элементы кроме одного нули). В то же время, неверно, что х^(k)0=(0,0,…,0,…), поскольку (х^(k),0) = 1 при всех k. Здесь ситуация аналогична предыдущему примеру: для сходимости в пространстве т нужна не просто покомпонентная сходимость, а равномерная покомпонентная сходимость.

3. Пространство сходящихся последовательностей с.

Элементами этого пространства являются сходящиеся последовательности х = (х₁,х₂,…,х_n,…) с расстоянием (х,у) = . Поскольку сходящиеся последовательности ограничены, пространствос является подпространством пространства т.

6. Пространства непрерывных функций L^p_с.

Рассмотрим (аналогично примеру 3) множество непрерывных функций, определенных на отрезке [0,1]. Расстояние между функциями определим формулой _p(х,у)=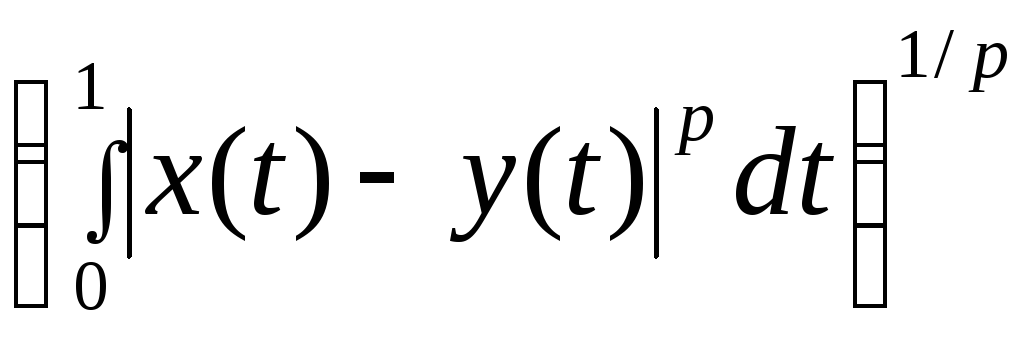, гдер1. Свойства расстояния следуют из свойств интеграла и неравенства Минковского. Сходимость может быть весьма экзотичной. Приведем пример последовательности непрерывных функций, которая в L^p_с сходится к 0 и при этом не сходится ни в одной точке интервала (0,1). Разобьем отрезок [0,1] на 3 равные части и обозначим через f₁(x) функцию, равную 0 в точках 0 и 1, равную 1 на отрезке [1/3, 2/3] и линейную на отрезках [0,1/3] и [2/3,1]. Затем разобьем отрезок на 4 равные части и обозначим через f₂(x) функцию, равную 0 на отрезке [3/4,1] и в точке 0, равную 1 на отрезке [1/4,1/2], линейную на отрезках [0,1/4] и [1/2,3/4] и через f₃(x) функцию, равную 0 на отрезке [0,1/4] и в точке 1, равную 1 на отрезке [1/2,3/4], линейную на отрезках [1/4,1/2] и [3/4,1]. Рекомендуется сделать рисунок. Продолжим подобное построение. При разбиении отрезка на п частей получим п – 2 новые функции, каждая из которых равна 1 на одном из внутренних промежутков, равна 0 на промежутках, с ним несмежных и линейная на смежных. Построенная последовательность обладает нужными странными свойствами (при любом p), в чем следует убедиться самостоятельно. (В частности для проверки сходимости в пространстве L^p_с достаточно оценить площадь между графиками функций и осью Ох).

7. Пространства последовательностей l^p.

Элементами этого пространства являются последовательности х=(х₁,х₂,…,х_n,…) такие, что ряд сходится. Например, как следует из курса математического анализа,, но в то же время. Расстояние вl^p определяется по формуле

_р(x,y)=. Из неравенства Минковского следуют сходимость ряда, который участвует в определении расстояния, и неравенство треугольника. Поскольку = _р(x,y), то из сходимости в l^p следует, что каждая компонента последовательностей сходится, т.е. из х⁽ⁿ⁾х⁽⁰⁾ следует, что при любомi. Обратное неверно - подходит пример, приведенный для пространства т.

7. Дискретные метрические пространства.

Рассмотрим произвольное множество и определим на нем расстояние таким образом, что (x,y)=1, если xy. В этом пространстве шар В(х, ) = В(х,1) (1 >  > 0) содержит только центр шара. Отсюда следует, что последовательность х_n сходится тогда и только тогда, когда начиная с некоторого номера ее члены совпадают.