
- •Предисловие
- •Введение. Предварительные сведения
- •Некоторые важные неравенства
- •Метрические пространства Определение и простейшие свойства
- •Последовательности и их пределы.
- •Примеры метрических пространств
- •Замыкания множеств. Замкнутые и открытые множества
- •Непрерывные отображения
- •Полные метрические пространства
- •Компактные метрические пространства
- •Линейные нормированные пространства Основные понятия и примеры
- •Изоморфные и изометричные линейные нормированные пространства
- •Компактность в линейных нормированных пространствах
- •Гильбертовы пространства
- •Линейные операторы Пространство линейных операторов
- •Сопряженные пространства и слабая сходимость
- •Три фундаментальные теоремы функционального анализа
- •Литература
- •Темы рефератов
- •Вопросы зачета
- •Указатель терминов и результатов
- •450000, Уфа-центр, ул. К.Маркса, 12
Три фундаментальные теоремы функционального анализа
В этом пункте формулируются три очень важные теоремы, доказательства можно найти в любом учебнике функционального анализа.
ТЕОРЕМА 16 (Хана-Банаха). Пусть Х – линейное нормированное пространство, L – линейное многообразие в Х, f – линейный непрерывный функционал на L. Тогда f можно продолжить до линейного непрерывного функционала F на Х такого, что ||F|| = ||f ||.
Не всякое непрерывное отображение можно продолжить на более обширное множество. Так, функцию sin(1/x), непрерывную на множестве положительных чисел, нельзя продолжить на множество неотрицательных чисел. В то же время, равномерно непрерывную функцию продолжить можно (упражнение 5.1). Линейный функционал является равномерно непрерывным и в этой части утверждение теоремы достаточно понятно. Сильнейшим является утверждение о возможности продолжения с сохранением нормы.
ТЕОРЕМА 17. (Банаха об обратном операторе). Если А – линейный непрерывный оператор, биективно отображающий банахово пространство Х на все банахово пространство Y, то оператор А имеет непрерывный обратный.
Ранее (п.) отмечалось, что отображение, обратное к непрерывному и взаимно однозначному, не обязано быть непрерывным. В задаче 3.15 утверждается, что это так для отображений компактных пространств. Теорема Банаха утверждает справедливость этого для линейных отображений банаховых пространств.
ТЕОРЕМА 18. (Банаха-Штейнхауза) Если последовательность {An} линейных операторов ограничена в каждой точке банахова пространства Х, т.е. ||Anх|| N(х), то нормы операторов ограничены, т.е. существует число M такое, что ||An|| M.
Упражнения
Докажите, что линейный функционал является равномерно непрерывным.
Операторы А,B:CC таковы: Ах =
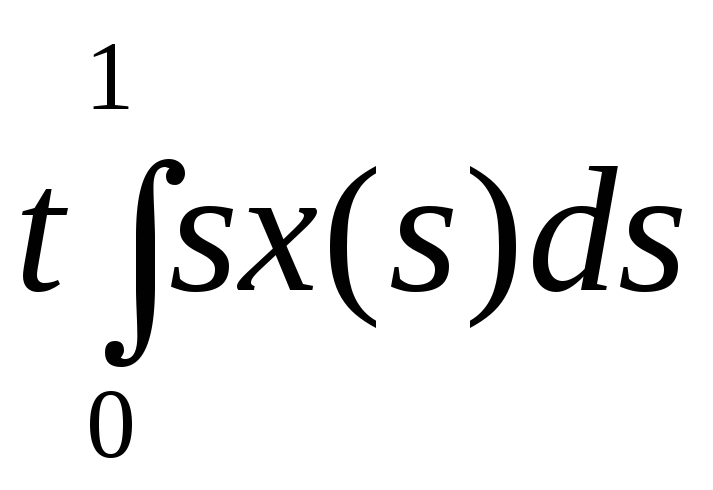 ,Bх
= tx(t).
Найдите нормы этих операторов и
докажите, что АB
BА.
,Bх
= tx(t).
Найдите нормы этих операторов и
докажите, что АB
BА.
На множестве всех вещественных многочленов определены операторы Ар = р, Bр = xр. Найдите оператор АBBА.
Докажите линейность, ограниченность и найдите норму функционала F:L2R, где Fх =
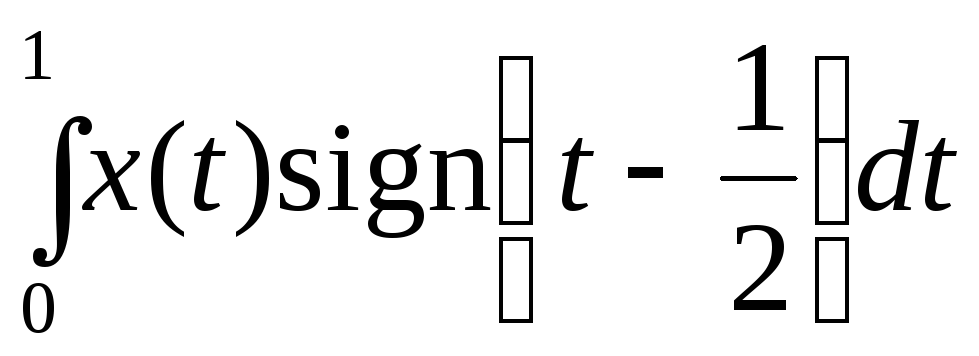 .
.Ядром линейного оператора называется прообраз нулевого элемента. Найдите ядра и образы операторов, отображающих l2l2, заданных формулами (х1, х2,…)(0,х1, х2,…); (х1, х2,…)(х2, х3,…); (х1, х2,…)(х1, х2/2, х3/3,…).
Пусть линейный функционал удовлетворяет условию
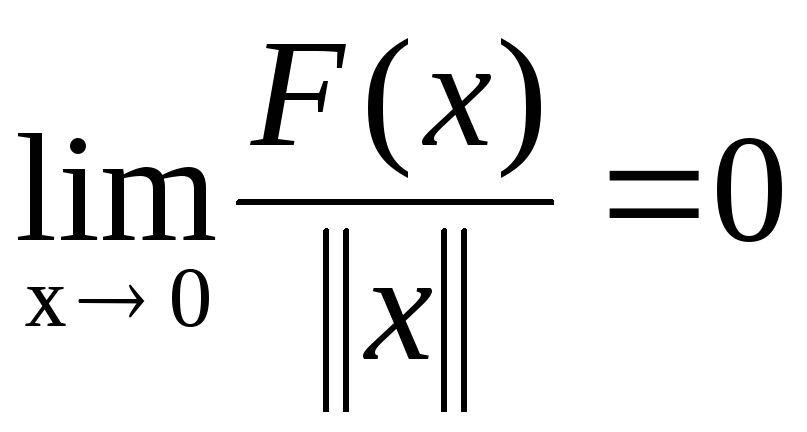 .
Докажите, чтоF(x)
= 0.
.
Докажите, чтоF(x)
= 0.Докажите, что линейный функционал, неотрицательный на некотором шаре, ограниченный.
Если в гильбертовом пространстве последовательность {хn} слабо сходится к х0 и ||хn|| ||х0||, то хn х0.
Если в гильбертовом пространстве последовательность {хn} слабо сходится к х0 и последовательность {yn} сходится по норме к y0, то (хn,yn)(х0,y0). Достаточно ли слабой сходимости последовательности {yn}?
Докажите, что в конечномерном пространстве слабая сходимость совпадает с сильной.
Литература
Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. Наука, 2002.
Люстерник Л.А., Соболев В.И. Краткий курс функционального анализа. Высшая школа, 1982.
Канторович Л.В., Акилов Г.П. Функциональный анализ. Наука, 1984.
Треногин В.А. Функциональный анализ. Высшая школа, 2002.
