
- •Предисловие
- •Введение. Предварительные сведения
- •Некоторые важные неравенства
- •Метрические пространства Определение и простейшие свойства
- •Последовательности и их пределы.
- •Примеры метрических пространств
- •Замыкания множеств. Замкнутые и открытые множества
- •Непрерывные отображения
- •Полные метрические пространства
- •Компактные метрические пространства
- •Линейные нормированные пространства Основные понятия и примеры
- •Изоморфные и изометричные линейные нормированные пространства
- •Компактность в линейных нормированных пространствах
- •Гильбертовы пространства
- •Линейные операторы Пространство линейных операторов
- •Сопряженные пространства и слабая сходимость
- •Три фундаментальные теоремы функционального анализа
- •Литература
- •Темы рефератов
- •Вопросы зачета
- •Указатель терминов и результатов
- •450000, Уфа-центр, ул. К.Маркса, 12
Сопряженные пространства и слабая сходимость
Линейный
оператор А:
XR
называется
линейным
функционалом.
Пространство L(X,
R)
банахово (п. ), поскольку пространство
вещественных чисел полное. Линейные
ограниченные функционалы будем обозначать
f(x).
Как и раньше, норма линейного функционала
определяется формулой
![]() .
.
ОПРЕДЕЛЕНИЕ 23. Пространство L(X, R) называется пространством, сопряженным к X и обозначается X*.
Опишем пространства, сопряженные к некоторым линейным нормированным пространствам.
Конечномерные пространства.
Если
(a1,…,an)
базис в п-мерном
пространстве L,
то линейный функционал f
однозначно
задается значениями (f(a1),…,
f(an)),
поскольку для любого вектора
![]() значение функционала задается формулой
значение функционала задается формулой![]() .
Мы будем использовать обозначениеfi
= f(ai).
Обратно, любой набор п
чисел (f1,…,
fn)
задает линейный оператор в п-мерном
пространстве описанным образом. Таким
образом, пространством, сопряженным с
п-мерным,
является также п-мерное
пространство. По сути, это описание на
новом языке факта, который излагался в
курсе линейной алгебры. Но теперь этого
мало: мы рассматриваем пространства,
наделенные нормой.
.
Мы будем использовать обозначениеfi
= f(ai).
Обратно, любой набор п
чисел (f1,…,
fn)
задает линейный оператор в п-мерном
пространстве описанным образом. Таким
образом, пространством, сопряженным с
п-мерным,
является также п-мерное
пространство. По сути, это описание на
новом языке факта, который излагался в
курсе линейной алгебры. Но теперь этого
мало: мы рассматриваем пространства,
наделенные нормой.
Докажем,
что при p
> 1
пространством,
сопряженным к
![]() ,
является пространство
,
является пространство![]() ,
где
,
где![]() Пусть (х1,…,хn)
координаты вектора х
в пространстве
L,
(f1,…,
fn)
– координаты вектора f
в сопряженном
пространстве. Тогда f(х)
=
Пусть (х1,…,хn)
координаты вектора х
в пространстве
L,
(f1,…,
fn)
– координаты вектора f
в сопряженном
пространстве. Тогда f(х)
=
![]() .
Применяя неравенство Гельдера для
конечных сумм (п. 2), получаем
.
Применяя неравенство Гельдера для
конечных сумм (п. 2), получаем
f(х)=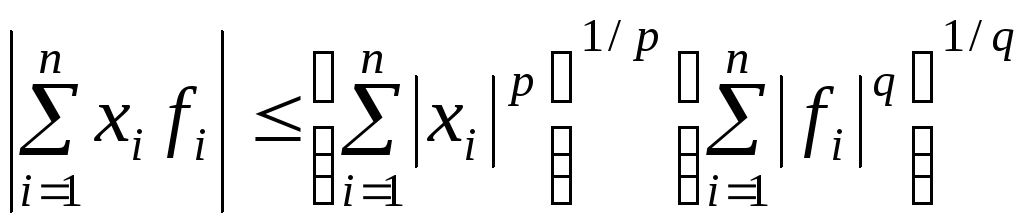 .
.
Если
||х||p
=
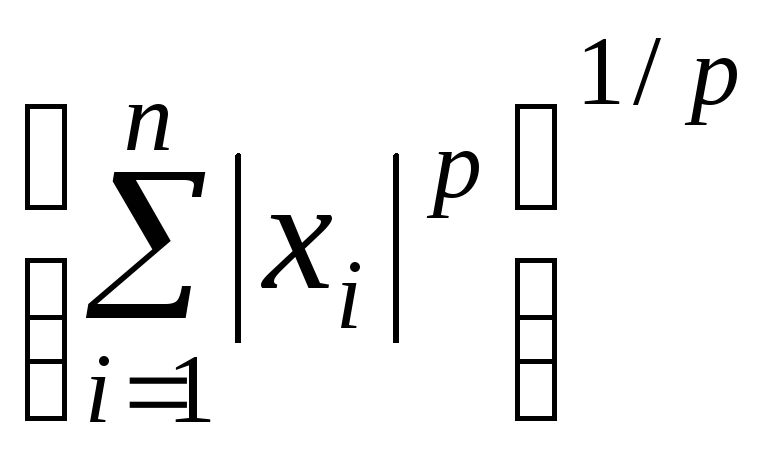 1,
1,
то
f(х)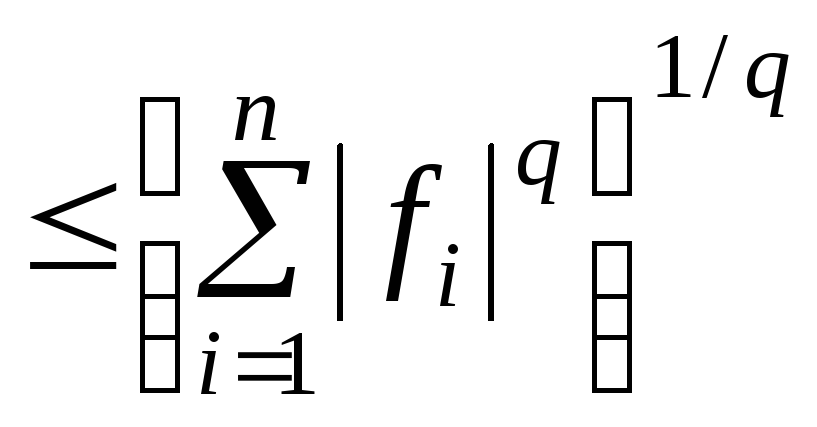 ,
,
т.е.
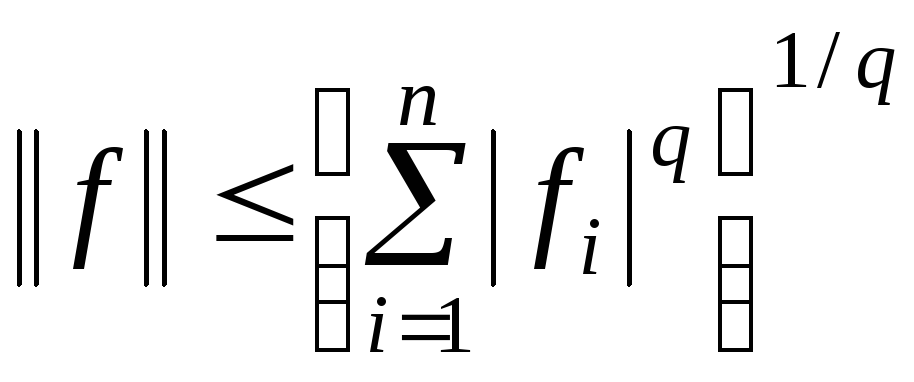 .
.
Для того чтобы убедиться, что в действительности имеет место равенство, найдем для данного ненулевого вектора f такой вектор х, что ||х||p = 1, f(х) = ||f||q. Положим
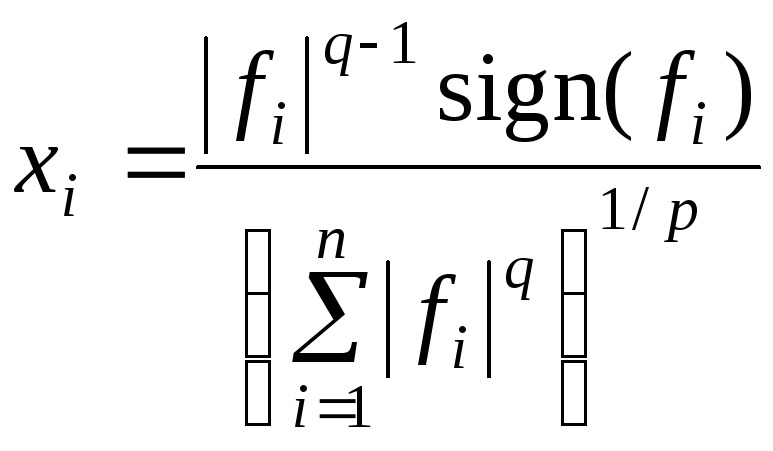 .
.
Напомним, что функция sign(a) (знак a) равна 1 для a положительных и 1 для a отрицательных. Тогда
||х||p
= ,
,
поскольку p(q1)=q. При этом
f(х)=
![]() =
=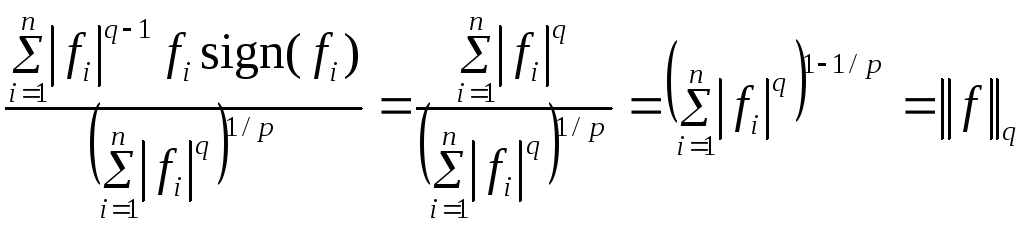 ,
,
что
и требовалось. Если p=2,
то и q=2,
т.е. пространство
![]() является сопряженным к самому себе.
Этот факт будет далее обобщен.
является сопряженным к самому себе.
Этот факт будет далее обобщен.
Сопряженным
к пространству
![]() является пространство
является пространство![]() .
Действительно,
.
Действительно,
f(х)=![]() ,
,
т.е.
![]() .
Для векторах
= (sign(f1),…,
sign(fn)),
у которого
||х||
=1, выполняется
равенство f(х)=
.
Для векторах
= (sign(f1),…,
sign(fn)),
у которого
||х||
=1, выполняется
равенство f(х)=
![]() ,
что и требовалось. Аналогично можно
установить и обратное: пространство
,
что и требовалось. Аналогично можно
установить и обратное: пространство![]() является сопряженным к
является сопряженным к![]() .
.
Пространства последовательностей.
Ограничимся
формулировками некоторых результатов.
При p>1
(lp)*=
lq,
где
![]()
(l1)*=m. При этом, m*l1.
Функциональные пространства.
Сопряженным к пространству С является пространство функций с ограниченной вариацией (подробности опускаем). К пополненному пространству Lp сопряженным является пространство Lq (p и q связаны обычным соотношением примера 1).
Гильбертовы пространства.
Докажем следующую теорему.
ТЕОРЕМА 15. Пространство, сопряженное к гильбертову пространству Н, изометрично Н.
ДОКАЗАТЕЛЬСТВО.
1. Пусть f:
Н
R
–ненулевой
линейный непрерывный функционал.
Докажем, что существует, причем
единственный, элемент fН,
для которого
f(х)=(f
, x)
(для нулевого функционала таким элементом
является нулевой). Пусть
L={x:
f(x)
= 0}
подпространство Н
(см. п. ).
Рассмотрим ортогональное дополнение
НL
(см. п. ) и
выберем ненулевой элемент х0
этого дополнения. Пусть f(х0)
=
0. Если f(х)
= ,
то
![]() =
= ![]() =0, т.е.
х
=0, т.е.
х![]() .Отсюда
следует, что любой вектор х
пространства Н
представим
в виде сх0+z,
где z
L.
Элемент f
будем искать в виде х0.
Тогда f(х0)
= (х0,х0)
= х02
= ,
= /х02.
Окончательно, по предыдущему х
=
.Отсюда
следует, что любой вектор х
пространства Н
представим
в виде сх0+z,
где z
L.
Элемент f
будем искать в виде х0.
Тогда f(х0)
= (х0,х0)
= х02
= ,
= /х02.
Окончательно, по предыдущему х
=
![]() +z
(zL).
Тогда (х0,х)
=
+z
(zL).
Тогда (х0,х)
= ![]() ,
существование вектора доказано. Для
доказательства единственности допустим,
что (f1,x)
= (f2,x)
при всех x.
Тогда (f1
f2,x)
= 0 и при x
= f1f2
из свойств скалярного произведения
получим f1f2=0.
Докажем теперь, что норма линейного
функционала f
равна норме
вектора f.
По
неравенству Коши-Буняковского (f,
x)
||f
||||x||,
это означает,
что норма функционала не превосходит
||f
||. Положив
x
= f/||f
||, убеждаемся,
что норма функционала совпадает с
||f
||.
,
существование вектора доказано. Для
доказательства единственности допустим,
что (f1,x)
= (f2,x)
при всех x.
Тогда (f1
f2,x)
= 0 и при x
= f1f2
из свойств скалярного произведения
получим f1f2=0.
Докажем теперь, что норма линейного
функционала f
равна норме
вектора f.
По
неравенству Коши-Буняковского (f,
x)
||f
||||x||,
это означает,
что норма функционала не превосходит
||f
||. Положив
x
= f/||f
||, убеждаемся,
что норма функционала совпадает с
||f
||.
2. Линейность любого функционала (f ,x) следует из определения скалярного произведения. Равенство его нормы норме вектора ||f|| доказано.
В линейных нормированных пространствах наряду с обычной можно ввести и иные виды сходимости.
ОПРЕДЕЛЕНИЕ 24. Последовательность {xn} в линейном нормированном пространстве слабо сходится к вектору x0, если для любого непрерывного функционала f справедливо утверждение f (xn) f (x0).
Из непрерывности функционала следует, что из условия xnx0 по норме (в старом смысле) следует слабая сходимость. Приведем пример, который показывает, что обратное неверно.
Рассмотрим
в гильбертовом пространстве l2
последовательность векторов х1=(1,0,…,0,…),
х2=(0,1,0,…,0,…),…
(у вектора хn
п-я
координата равна единице, остальные
нулевые). Отмечалось (п. ), что эта
последовательность не сходится в метрике
пространства l2.
Пусть fl2.
Тогда (f,хn)=
fn0,
поскольку ряд
![]() сходится. Тем самымхn
слабо
сходится к 0.
сходится. Тем самымхn
слабо
сходится к 0.
