
- •Предисловие
- •Введение. Предварительные сведения
- •Некоторые важные неравенства
- •Метрические пространства Определение и простейшие свойства
- •Последовательности и их пределы.
- •Примеры метрических пространств
- •Замыкания множеств. Замкнутые и открытые множества
- •Непрерывные отображения
- •Полные метрические пространства
- •Компактные метрические пространства
- •Линейные нормированные пространства Основные понятия и примеры
- •Изоморфные и изометричные линейные нормированные пространства
- •Компактность в линейных нормированных пространствах
- •Гильбертовы пространства
- •Линейные операторы Пространство линейных операторов
- •Сопряженные пространства и слабая сходимость
- •Три фундаментальные теоремы функционального анализа
- •Литература
- •Темы рефератов
- •Вопросы зачета
- •Указатель терминов и результатов
- •450000, Уфа-центр, ул. К.Маркса, 12
Изоморфные и изометричные линейные нормированные пространства
В курсе линейной алгебры определялось понятие изоморфизма линейных пространств. Линейные пространства Х и Y называются изоморфными, если существует взаимно однозначное отображение А: ХY такое, что А(х1+х2) = А(х1) +А(х2), А(х) = А(х). Отсюда следует, что семейство векторов {a1,a2,…,an} является базисом в пространстве Х тогда и только тогда, когда {Аa1, Аa2,…, Аan} – базис в пространстве Y. В курсе линейной алгебры доказано, что для изоморфизма конечномерных линейных пространств необходимо и достаточно совпадение их размерностей.
Для линейных нормированных пространств в понятие изоморфизма естественно включается и непрерывность.
ОПРЕДЕЛЕНИЕ 17. Пусть Х, Y линейные нормированные пространства. Отображение А: ХY называется линейным (синоним: линейным оператором), если А(х1+х2) = А(х1) + А(х2), А(х) = А(х). Линейный оператор А называется изоморфизмом, если у него существует обратный и отображения А и А1 непрерывные. Пространства Х, Y называются изоморфными, если существует изоморфизм А: ХY.
Очевидно, что отношение изоморфизма линейных нормированных пространств является отношением эквивалентности, т.е. обладает свойствами рефлексивности, симметричности и транзитивности (эти понятия рассматривались в курсе математического анализа).
Изоморфизм
сохраняет замкнутость и открытость
множеств как взаимно непрерывное
отображение (п. ) и компактность (п. ). В
общем случае при непрерывных отображениях
не сохраняется ограниченность множеств
(например, функция
![]() переводит ограниченное множество (0,1]
в неограниченное [1,)).
Для линейных операторов справедливо
следующее утверждение, полезное и в
главе 5.
переводит ограниченное множество (0,1]
в неограниченное [1,)).
Для линейных операторов справедливо
следующее утверждение, полезное и в
главе 5.
ПРЕДЛОЖЕНИЕ 14. Если А: ХY линейное непрерывное отображение и МХ – ограниченное множество, то множество А(М) также ограниченное.
ДОКАЗАТЕЛЬСТВО. Ограниченность множества М означает, что при некотором значении d нормы всех точек из М не превосходят d. Пусть напротив множество А(М) не является ограниченным. Это означает, что для любого натурального n существует точка хnМ такая, что ||А(хn)|| >n. Рассмотрим точки yn=хn/n. Тогда ||yn|| = ||хn/n|| = ||хn||/n /n d/n0, т.е. yn0. Но при этом ||А(yn)|| = ||А(хn/n)|| = ||А(хn)||/n >1, т.е. неверно, что А(yn)0, что противоречит непрерывности оператора А.
Для конечномерных линейных нормированных пространств справедливо следующее утверждение.
ТЕОРЕМА 7. Любые два n – мерных линейных нормированных пространства изоморфны.
ДОКАЗАТЕЛЬСТВО.
В силу отмеченной транзитивности
достаточно доказать, что любое n
– мерное линейное нормированное
пространство Х
изоморфно евклидову пространству
![]() .
Так удобно поступить, поскольку в
линейной алгебре свойства этого
пространства изучены достаточно
подробно. Выберем в пространствеХ
некоторый базис {a1,
a2,…,
an}.
Любой вектор хХ
единственным образом представим в виде
х=
.
Так удобно поступить, поскольку в
линейной алгебре свойства этого
пространства изучены достаточно
подробно. Выберем в пространствеХ
некоторый базис {a1,
a2,…,
an}.
Любой вектор хХ
единственным образом представим в виде
х=![]() .
ОтображениеА:Х
.
ОтображениеА:Х![]() определим формулойА
определим формулойА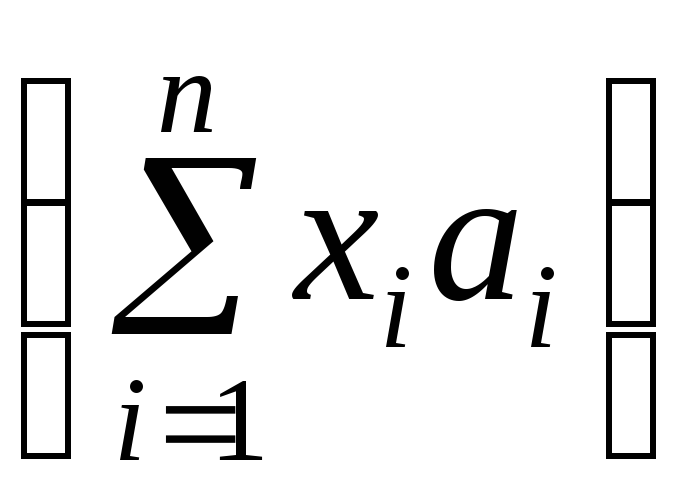 =(х1,
х2,…,
хn).
Очевидно, что отображение А
взаимно однозначное и обладает свойствами
А(х1+х2)
= А(х1)
+ А(х2),
А(х)
= А(х).
Необходимо проверить непрерывность
отображений А
и А1.
=(х1,
х2,…,
хn).
Очевидно, что отображение А
взаимно однозначное и обладает свойствами
А(х1+х2)
= А(х1)
+ А(х2),
А(х)
= А(х).
Необходимо проверить непрерывность
отображений А
и А1.
Из свойств нормы,
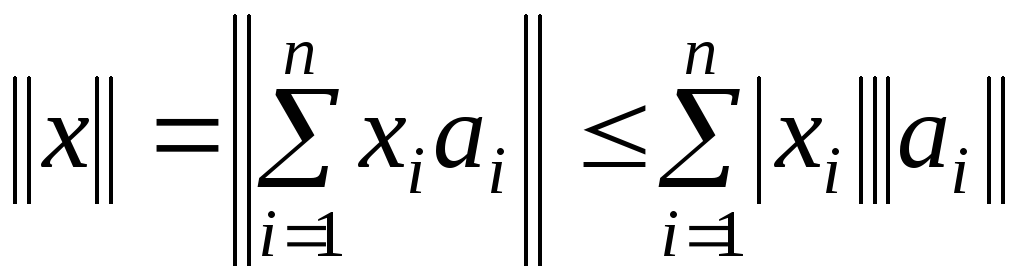 .
Неравенство Коши-Буняковского имеет
вид
.
Неравенство Коши-Буняковского имеет
вид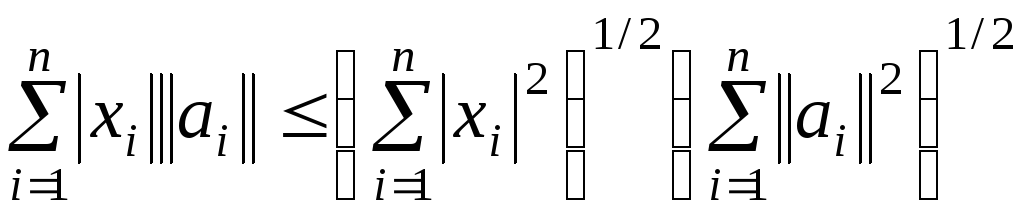 .
Если ввести обозначение=
.
Если ввести обозначение= ,
то полученное неравенство примет вид
,
то полученное неравенство примет вид
 .
Отсюда, изАхnАх0
следует, что хnх0,
т.е отображение А1
является непрерывным.
.
Отсюда, изАхnАх0
следует, что хnх0,
т.е отображение А1
является непрерывным. Рассмотрим евклидову сферу S={y:
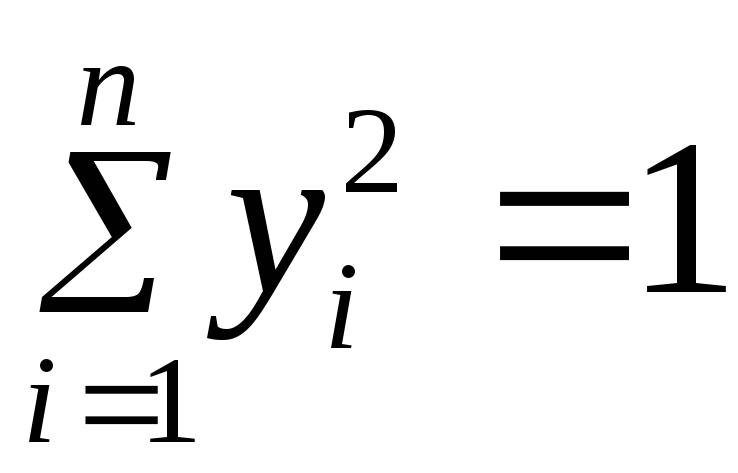 }
в евклидовом пространстве
}
в евклидовом пространстве и рассмотрим функциюf:
SR,
заданную формулой f(y)
=
и рассмотрим функциюf:
SR,
заданную формулой f(y)
=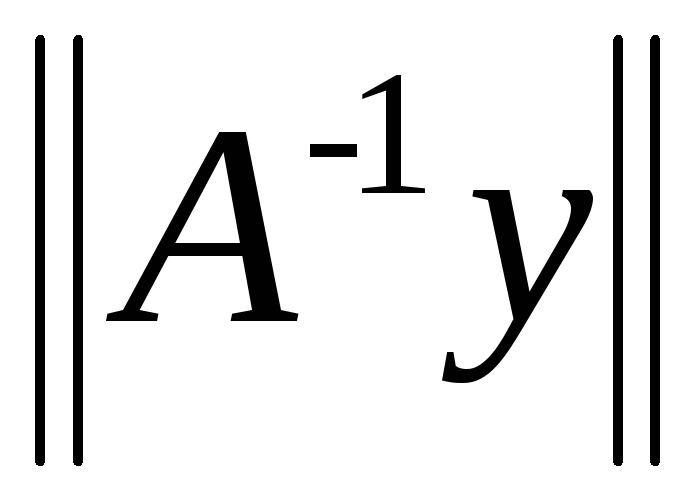 .
Поскольку отображениеА
биективное,
то f(y)
> 0 при y
0 (при отображении А
нулевому элементу Х
соответствует нулевой элемент
.
Поскольку отображениеА
биективное,
то f(y)
> 0 при y
0 (при отображении А
нулевому элементу Х
соответствует нулевой элемент
 ).
По доказанному отображениеА1
непрерывное, по предложению 11 норма
также является непрерывным отображением.
Таким образом, функция f
непрерывна
как суперпозиция непрерывных отображений
(п.). Далее, сфера является замкнутым и
ограниченным подмножеством евклидова
пространства (убедитесь в этом
самостоятельно). А тогда по теореме 3
сфера является компактным подмножеством
евклидова пространства. По теореме 4
функция f
достигает на S
наименьшего значения .
Из предыдущего следует, что
> 0. Тогда f(y)
.
Если теперь y
произвольный ненулевой элемент
).
По доказанному отображениеА1
непрерывное, по предложению 11 норма
также является непрерывным отображением.
Таким образом, функция f
непрерывна
как суперпозиция непрерывных отображений
(п.). Далее, сфера является замкнутым и
ограниченным подмножеством евклидова
пространства (убедитесь в этом
самостоятельно). А тогда по теореме 3
сфера является компактным подмножеством
евклидова пространства. По теореме 4
функция f
достигает на S
наименьшего значения .
Из предыдущего следует, что
> 0. Тогда f(y)
.
Если теперь y
произвольный ненулевой элемент
 ,
тоy/
,
тоy/ .
Тем самым f(y/
.
Тем самым f(y/
> 0. Из свойств нормы и свойств
изоморфизма получим неравенство
> 0. Из свойств нормы и свойств
изоморфизма получим неравенство

.
Тем самым, справедливо неравенство
.
Тем самым, справедливо неравенство

 (очевидно, что это неравенство справедливо
и при y=0).
Полагая y=Ах,
получим неравенство
(очевидно, что это неравенство справедливо
и при y=0).
Полагая y=Ах,
получим неравенство
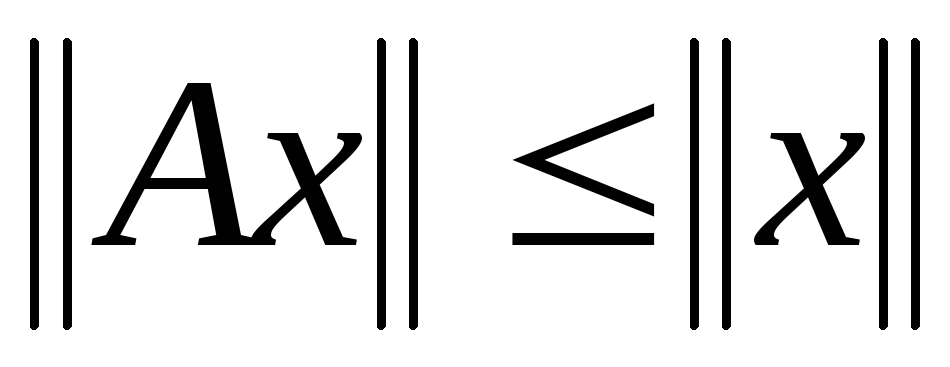 /.
А это означает непрерывность отображения
А.
Теорема доказана.
/.
А это означает непрерывность отображения
А.
Теорема доказана.
Из
этой теоремы вытекают важные следствия.
Поскольку пространство
![]() полное (п.), то в силу изоморфизма (он
сохраняет сходимость) этим свойством
обладает и всякое конечномерное линейное
нормированное пространство. А отсюда
(см. задачу 3.16) следует, что конечномерное
линейное многообразие в линейном
нормированном пространстве является
замкнутым, т. е. подпространством. Для
бесконечномерных многообразий это не
так. Например, рассмотрим в пространствеС
множество всех многочленов. Оно является
линейным многообразием, причем не
совпадает с пространством С.
Например, функция
полное (п.), то в силу изоморфизма (он
сохраняет сходимость) этим свойством
обладает и всякое конечномерное линейное
нормированное пространство. А отсюда
(см. задачу 3.16) следует, что конечномерное
линейное многообразие в линейном
нормированном пространстве является
замкнутым, т. е. подпространством. Для
бесконечномерных многообразий это не
так. Например, рассмотрим в пространствеС
множество всех многочленов. Оно является
линейным многообразием, причем не
совпадает с пространством С.
Например, функция
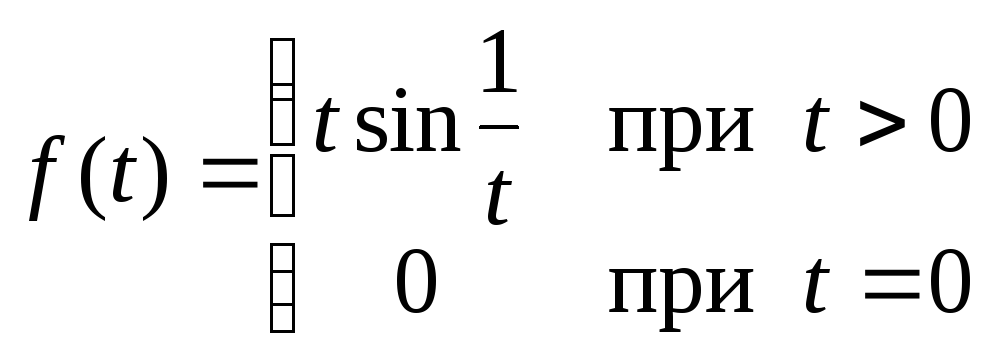
является элементом пространства С (проверьте это), но многочленом не является, поскольку имеет бесконечное множество корней. В то же время, по известной из математического анализа теореме Вейерштрасса любая непрерывная функция на отрезке является пределом равномерно сходящейся последовательности многочленов, т.е. в терминологии метрических пространств замыкание многообразия многочленов совпадает со всем пространством С. Значит, линейное многообразие многочленов не является подпространством.
Понятие изометричности является более сильным.
ОПРЕДЕЛЕНИЕ 18. Метрические пространства Х, Y называются изометричными, если существует биективное отображение f: ХY, сохраняющее расстояния, т.е. такое, что (x,y) = (f(x), f(y)) (изометрия). Линейные нормированные пространства называются изометричными, если существует изоморфизм линейных пространств, сохраняющий нормы векторов (а тогда и расстояния). Такой изоморфизм называется изометрией.
С точки зрения функционального анализа изометричные линейные нормированные пространства обладают одними и теми же свойствами.
Заключение
теоремы 6 при замене изоморфизма на
изометрию не выполняется. Например,
пространства
![]() не изометричны при различныхр.
Проверим это в частном случае п=2;
р=1,
р=2.
Пусть напротив изометрия f
существует. Рассмотрим в пространстве
не изометричны при различныхр.
Проверим это в частном случае п=2;
р=1,
р=2.
Пусть напротив изометрия f
существует. Рассмотрим в пространстве
![]() векторых=(1,0)
и y=(0,1).
По определению нормы,
векторых=(1,0)
и y=(0,1).
По определению нормы,
![]() .
.
Тогда должны выполняться равенства
![]() .
.
Если f(x) = (x1,x2), f(y) = (y1,y2), то из свойств линейного изоморфизма
![]() .
.
Отсюда, должны выполняться равенства
x12+x22=1,
y12+y22=1,
![]() .
.
Если первые два равенства умножить на 2 и сложить, а затем вычесть третье, умноженное на 4, получим равенство (х1 y1)2 + (x2 y2)2 = 0. Последнее равенство возможно лишь при х1 = y1 и x2 = y2, т.е. f(x) = f(y). А это противоречит биективности f.
