1.3.3.2 Алгебраический критерий устойчивости (аналог критерия Гурвица)

Для оценки устойчивости импульсных систем управления используют билинейное или -преобразование, посредством которого окружность единичного радиуса (рис. 1.17) отображается на мнимую плоскость комплексной величины (рис.1.19). Преобразование осуществляют заменой оператора z оператором w согласно равенству

. (1.11)

Названную замену операторов часто в англоязычной литературе называют преобразованием Тастина (Tustin). Характеристическое уравнение САУ (1.10) в результате подстановки в него (1.11) и приведения подобных членов приобретает следующий вид

(1.12)

Например, при m=1 характеристическое уравнение САУ имеет простейший вид

где и . Это уравнение можно теперь исследовать с помощью критерия Гурвица. Из теории непрерывных систем известны необходимые и достаточные условия устойчивости САУ первого порядка в виде двух неравенств и

При m=2 условия устойчивости САУ второго порядка выражаются тремя неравенствами ; ; и т.д.

1.3.3.3 Алгебраический критерий Шур-Кона

Критерий Шур-Кона также позволяет оценить устойчивость замкнутой импульсной САУ по ее характеристическому уравнению (1.10). Для этого формируют следующую последовательность определителей, составленных из коэффициентов характеристического уравнения

, ; ,

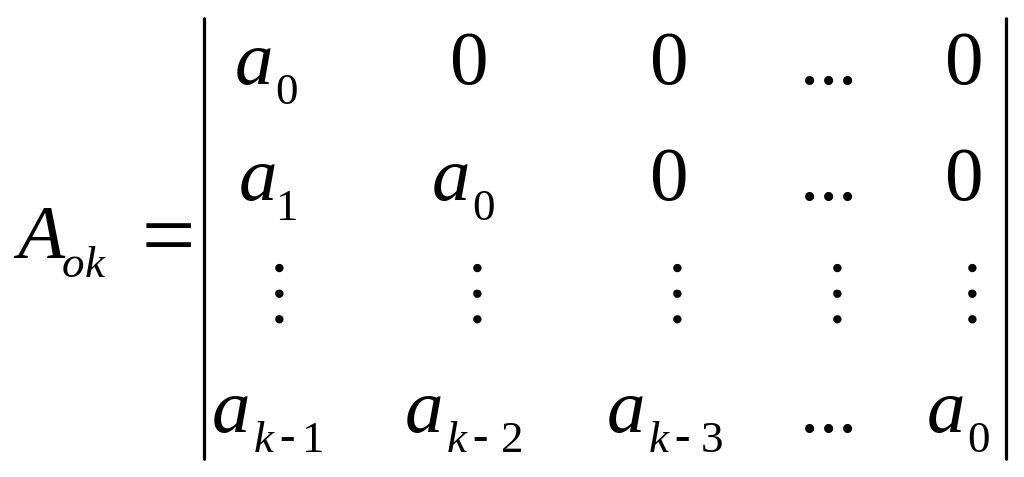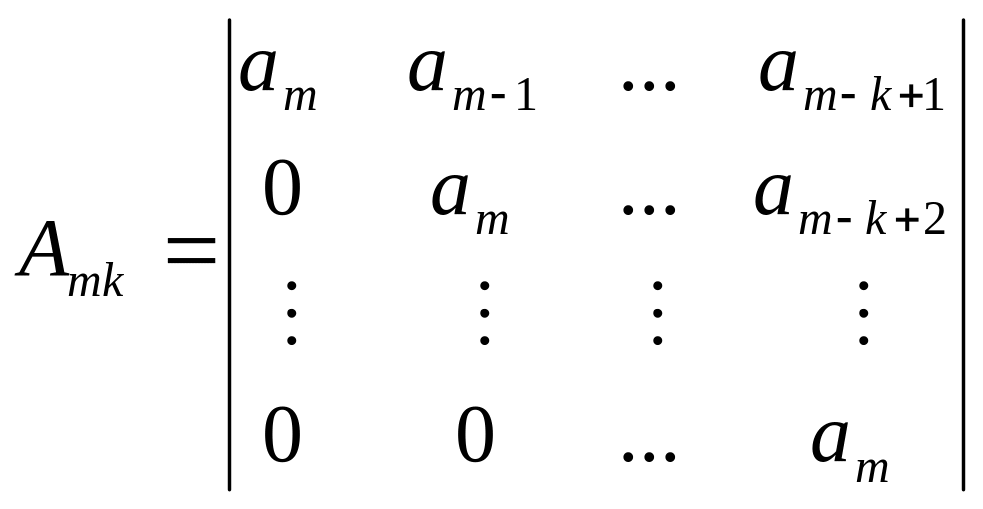где k=1,2…m; m-порядок характеристического уравнения.

Для того, чтобы импульсная САУ была устойчивой, все корни характеристического уравнения должны лежать внутри круга единичного радиуса. Это означает, что количество перемен знака в последовательности определителей 1, , , …, должно быть равно m, где m-порядок характеристического уравнения. Критерий устойчивости может быть сформулирован иначе следующим образом:

, если k – нечетное число;

, если k- четное.

Например, при m=2 для последовательности определителей 1, и должны выполняться следующие неравенства:

; ,

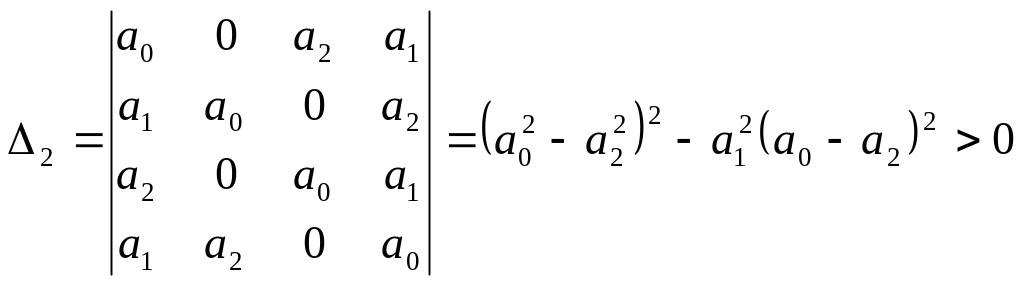указывающие на необходимость двух перемен знака для того, чтобы два корня характеристического уравнения лежали внутри круга единичного радиуса.

1.3.4 Аналог критерия Михайлова

Под аналогом критерия Михайлова понимают совокупность признаков устойчивости импульсной САУ, которые находят в результате исследования характеристического полинома замкнутой системы D(z), см. уравнение (1.10). Порядок анализа аналогичен методике исследования непрерывной САУ.

Более простой считают графическую интерпретацию критерия с построением годографа Михайлова. При этом сначала в характеристическом полиноме D(z) производят замену оператора z на , где -угловая частота входного сигнала. В результате чего получают уравнение годографа Михайлова.

.

Затем это уравнение преобразуют и записывают в алгебраическом или показательном виде для построения годографа. С использованием декартовых координат уравнение приобретает алгебраический вид

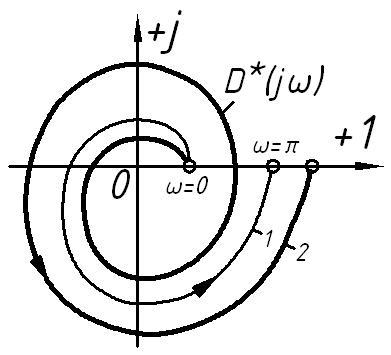
Поскольку ЧХ импульсных систем являются периодическими функциями частоты, годограф Михайлова строят в диапазоне частот . На рисунке 1.19 показан примерный вид годографов 1и 2 импульсной САУ второго (m=2) и четвертого (m=4) порядков соответственно.

Критерий устойчивости Михайлова формулируют следующим образом: для устойчивости импульсной САУ необходимо, чтобы годограф начинался ( ) на положительной действительной полуоси комплексной q- плоскости и охватывал начало координат, последовательно проходя 2m квадрантов,

m-порядок системы управления.

Таким образом, изображенные на рисунке 1.19 годографы принадлежат устойчивым САУ. Действительно, годограф 1 проходит через четыре квадранта (2m=4),а годограф 2- через восемь (2m=8). В отличии от непрерывных систем годограф импульсной САУ не уходит в бесконечность, а заканчивается на вещественной полуоси , проходя при этом в два раза больше квадрантов.

Рисунок 1.19