Задача № 1
В урне находятся
белых,
красных и
синих шаров. Найти вероятность вынуть
из урны белый шар? Цветной шар? Из урны
наугад взяли
шаров. Какова вероятность того, что
среди них имеется
белых,
красных и
синих шаров? Какова вероятность того,
что среди них окажется хотя бы один
синий шар? Из урны взят шар, определен
его цвет и шар возвращен обратно в урну.
Таким образом, взято
шаров. Найти вероятность того, что среди
них окажется хотя бы одни шар r-того
цвета.
Решение задачи
Найдем общее число шаров в урне:
.
Общее число
независимых исходов очевидно равно
числу шаров в урне, то есть
.
Число благоприятных исходов для белых
шаров равно:
.
По формуле классической вероятности
вытянуть белый шар – событие А
имеем:
.
Цветными шарами будут красный и синий шары. Найдем вероятности вытянуть красный и синий шар. Для красных шаров имеем и . Тогда вероятность вытянуть красный шар – событие В по формуле классической вероятности равна:
.
Для вероятности вынуть синий шар (событие С) имеем ; и получим по формуле классической вероятности:
.
По теореме о сложении вероятностей независимых событий имеем для вероятности вынуть цветной шар (событие D):
.
Найдем вероятность того, что среди
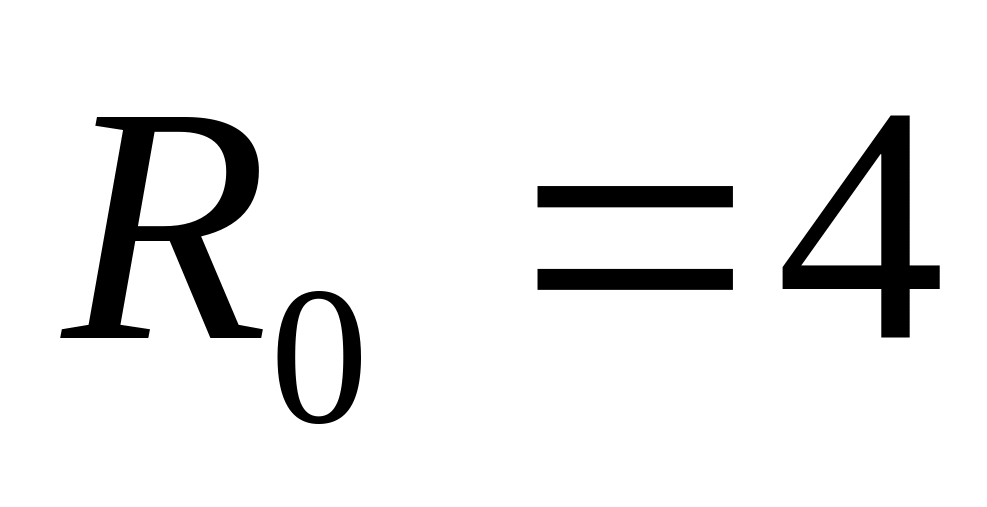шаров имеются
белых;
красный и
синий? Очевидно, что общее число
независимых исходов равно числу
комбинаций по
шаров из
шаров. Согласно формуле комбинаторики
имеем:
.
Число благоприятных исходов для белых шаров будет равно числу комбинаций из белых шаров по белым шарам, то есть:
.
Число благоприятных исходов для красных шаров будет равно числу комбинаций из красных шаров по красному шару, то есть:
.
Число благоприятных исходов для синих шаров будет равно числу комбинаций из синих шаров по синих шаров, то есть:
.
Общее число благоприятных исходов будет
равно произведению
,
так как каждая комбинация шаров одного
цвета повторяется столько раз, сколько
имеется комбинаций других цветов, то
есть:
.
Окончательно по формуле классической вероятности имеем для вероятности того, что среди шаров два белых, один красный и один синий:
.
Вероятность появления хотя бы одного события из
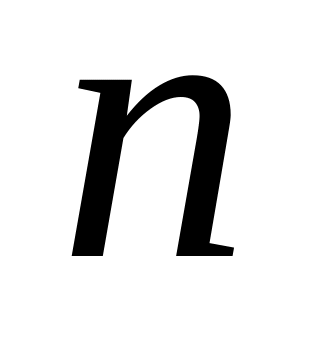событий независимых в совокупности
равна:
,
где
- вероятность противоположного события.
Так как в условии задачи указано, что
вынимается синий шар, то
- это вероятность вытянуть не синий шар.
Рассчитаем число не синих шаров в урне:
шаров. Из урны вынимаются
шара и поэтому общая формула запишется
так:
;
Рассчитаем вероятности
вытянуть из урны не синий шар. Так как
для вынимания первого шара имеем в урне
15 не синих шаров при общем количестве
шаров в урне 20, то по формуле классической
вероятности имеем:
.
При вынимании второго шара в урне имеется
уже
шаров из них не синих шаров
,
то по формуле классической вероятности
имеем:
.
По аналогии получаем для
и
:
;
.
Подставляя полученные значения в формулу имеем:
.
Так как число шаров в урне не меняется, то для вероятности появления хотя бы одного события имеем формулу:
где
-вероятность
противоположного события.
В условии задачи указано, что вынимается синий шар, и - вероятность вытянуть не синий шар. Из урны вынимают шар раза подряд и каждый раз возвращают в урну, поэтому общая формула запишется так:
Так как число не синих шаров равно 15,то
Подставляя полученные значения в формулу, имеем:
Ответ:
.