Задача № 6

По имеющейся выборке построить вариационный ряд. Для полученного вариационного ряда найти моду Мо, медиану Ме, размах R, среднее выборочное , исправленную выборочную дисперсию (x), выборочное среднее квадратичное отклонение и коэффициент вариации. Найти доверительные пределы для истинного значения «а» и истинного среднего квадратического отклонения « » для генеральной совокупности для .

По имеющемуся вариационному ряду построить интервальный ряд. По полученному интервальному ряду проверить статистическую гипотезу о том, что генеральная совокупность имеет нормальный закон распределения, по критерию согласия Пирсона «хи - квадрат» для уровня значимости .

Решение

Условие задачи: В результате случайного отбора 60 показателей по потреблению белков в сутки человеком получено, г:

76,5; 79,0; 85,5; 84,7; 77,0;89,9; 95,0; 84,0; 87,8; 85,0;

84,5; 82,0; 92,6; 82,8; 90,0; 78,5; 82,6; 97,0; 93,5; 89,0;

78,5; 88,5; 87,0; 94,5; 88,0; 89,8; 88,0; 89,5; 94,0; 99,0;

96,0; 91,0; 89,5; 91,0; 83,5; 91,0; 93,0; 88,5; 90,5; 92,0;

76,6; 90,0; 95,6; 80,0; 98,0; 86,0; 87,0; 89,5; 80,0; 83,5;

90,8; 89,0; 88,0; 98,4; 81,5; 93,0; 90,0; 95,0; 90,7; 86,0.

1. По имеющейся выборке составим вариационный ряд, т. е. расположим все элементы упорядоченно по возрастанию величины:

76,5<76,6<77,0<78,5<79,0<80,0 80,0<81,5<82,0<82,6<82,8<83,5 83,5<84<84,5<84,7<85,0<85,5<86,0 86,0<96,5<87,0 87,0<87,5<87,8<88,0 88,0<88,5 88,5<89,0 89,0<89,5 89,5 89,5<89,8<89,9<90,0 90,0 90,0<90,5<90,7<90,8<91,0 91,0 91,0<92<92,6<93,0<93,0<93,5<94,0<94,5<95,0 95,0<95,6<96,0<97,0<98,0<98,4<99,0.

2. Найдем моду вариационного ряда, т. е. то значение варианты, которое встречается в вариационном ряду чаще всего:

Мо = 88,0; 89,5; 90,0; 91,0 – распределение выборки многомодальное.

3. Найдем медиану, т. е. ту варианту, которая лежит посредине вариационного ряда:

В случае n=2k – четного числа вариант имеем:

Ме =

В случае если n=2k – нечетного числа вариант Ме =

4. Найдем размах вариационного ряда, т. е. разность между последним и первым членом вариационного ряда:

R = =99,0-76,5=22,5

5. Найдем среднее выборочное :

=

6. Возведем члены вариационного ряда в квадрат:

5852,25<5867,56<5929,0<6162,25<6241,0<6400,0 6400<6642,25<6724,0<6822,76<

6855,84<6972,25 6972,25<7056,0<7140,25<7174,09<7225<7310,25<7396,0<7482,25<7569,0<7656,25<7708,84<7744,0 7740,0 7740<7832,25 7832,25<7921,0 7921,0<8010,25< 8010,25<8064,04<8082,01<8100,0 8100,0 8100,0<8190,25<8226,49<8244,64<8281,0 8281,0 8281,0<8464,0<8574,76<8649,0 8649,0<8742,25<8836,0<8930,25<9025,0<9025<9139,36<9216,0<9409,0<9604,0<9622,56<9801,0.

7. Найдем исправленную выборочную дисперсию (x):

(x)= =

8. Найдем исправленное среднее выборочное квадратичное отклонение:

=

9. Найдем коэффициент вариации V(x), %:

V(x)

10. Найдем доверительные интервалы для «а» и « »:

а) - ; . Значение находим по таблице 4 Приложения для и n = 60.

-

б) ; ; n = 60; q=0,188

Значение q находим по таблице 4 Приложения для и n = 60.

11. Найдем число интервалов интервального ряда m:

m

Значение m округляем до ближайшего наименьшего целого.

12. Найдем ширину интервала h:

h=

Округление производится до высшего десятичного знака т. е. 7,333 7,34

12. Найдем границы интервалов:

1 интервал: ( ) (76,5; 80,34)

2 интервал: ( ) (80,34; 84,08)

3 интервал: ( ) (84,08; 87,82)

4 интервал: ( ) (87,82; 91,56)

5 интервал: ( ) (91,56; 95,30)

6 интервал: ( ) (95,30; 99,04)

12. Запишем интервальный ряд:

Интер-вал					)
n

где: n - число вариант, попадающих в i-тый интервал

Если какое-либо <6, то данный интервал объединяется с последующим и предыдущим. Число интервалов уменьшается при этом на единицу, а границы интервалов объединяются.

12. Рассчитаем теоретические вероятности для интервалов в предположении, что распределение генеральной совокупности имеет нормальный закон:

; где: - верхняя граница i-того интервала; - нижняя граница i-того интервала.

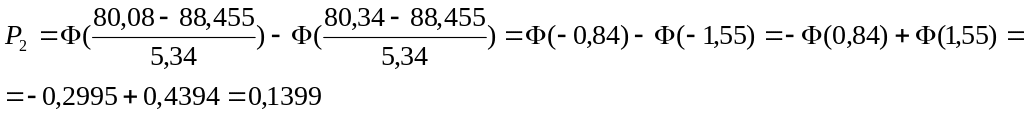
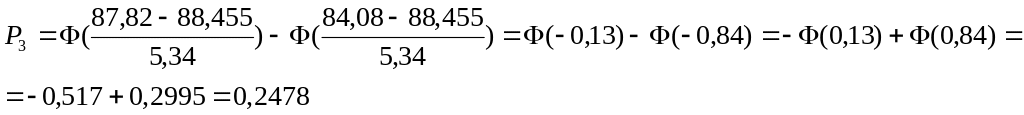
12. Рассчитаем теоретические частоты :

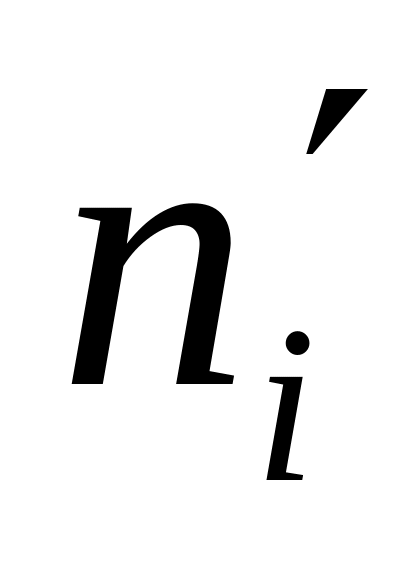= = 0,0487*60 = 2,92

= = 0,1399*60 = 8,39

= = 0,2478*60 = 14,87

= = 0,2707*60 = 16,24

= = 0,1825*60 = 10,95

= = 0,0757*60 = 4,54

12. Найдем наблюдаемое значение критерия Пирсона «хи - квадрат» 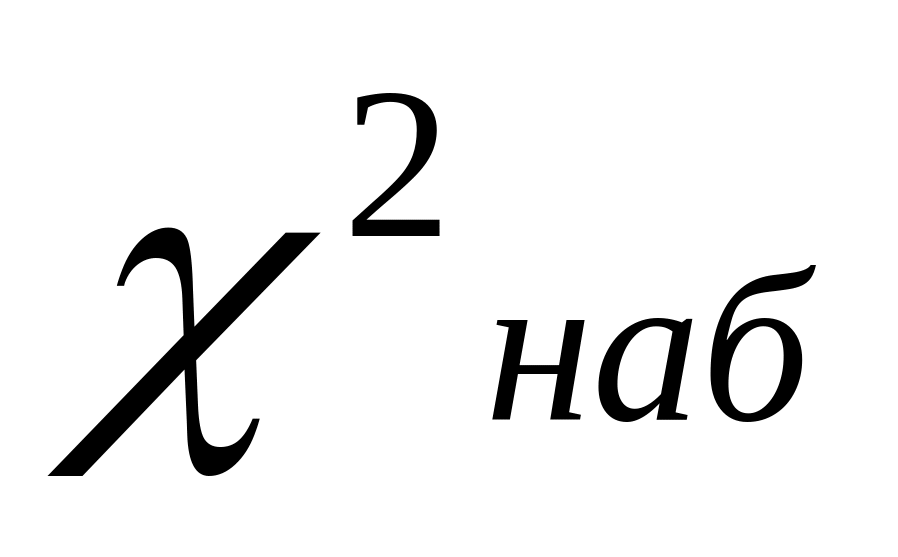. Для этого данные занесем в следующую таблицу, по которой и произведем необходимые действия.

№ п/п	n				/
1. 2. 3. 4. 5. 6.	6 7 10 22 9 6	2,92 8,39 14,87 16,24 10,95 4,54	3,08 -1,39 -4,87 5,76 -1,95 1,46	9,4864 1,9321 23,7169 33,1776 3,8025 2,1316	3,25 0,23 1,59 2,04 0,35 0,47
				=	7,93

=7,93

12. Для уровня значимости 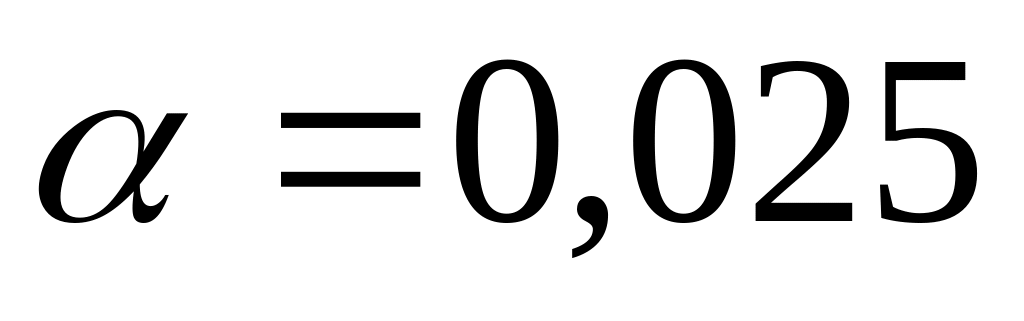и числа степеней свободы k=m-z-1, где z=2 – число параметров нормального распределения, - по таблице 5 (критических значений 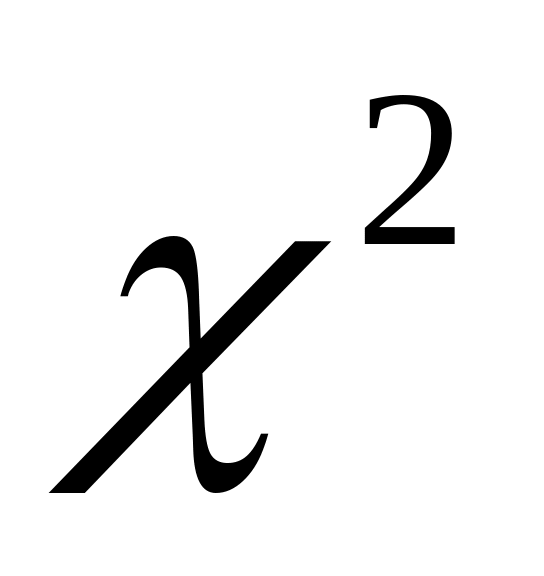). Приложения находим критическое значение .

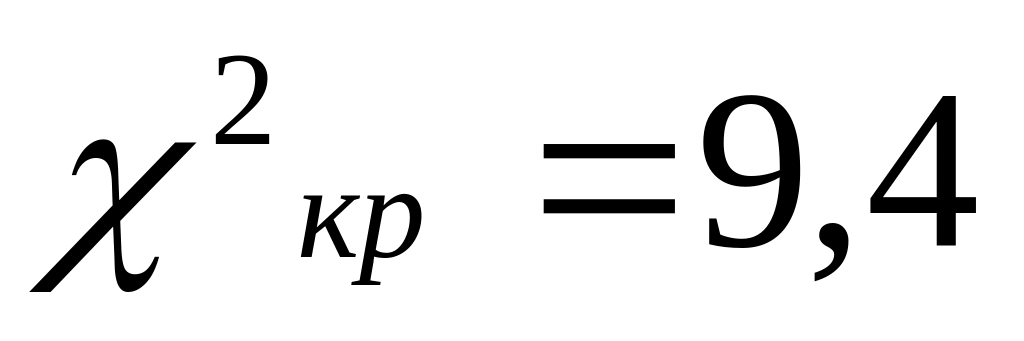Вывод: Так как =7,93< , то распределение генеральной совокупности значимо является нормальным.

Если > , то делается вывод о том, что распределение генеральной совокупности не подчиняется нормальному закону.