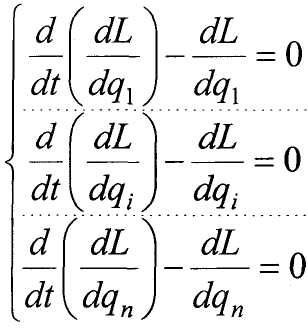- •Динамика
- •1. Введение в динамику. Законы динамики.
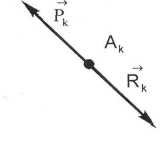
- •Импульс силы
- •4. Относительное движение материальной точки.
- •Здесь – абсолютное ускорение точки по отношению к о.С.О. По теореме Кориолиса
- •8. Принцип Германа-Эйлера-д'Аламбера.
- •Динамики
- •Прямолинейные колебания материальной точки. Некоторые виды колебаний.
- •На материальную точку действуют и
- •Проанализируем амплитуду вынужденных колебаний:
Динамики
(П. В. П. и О. У. .)
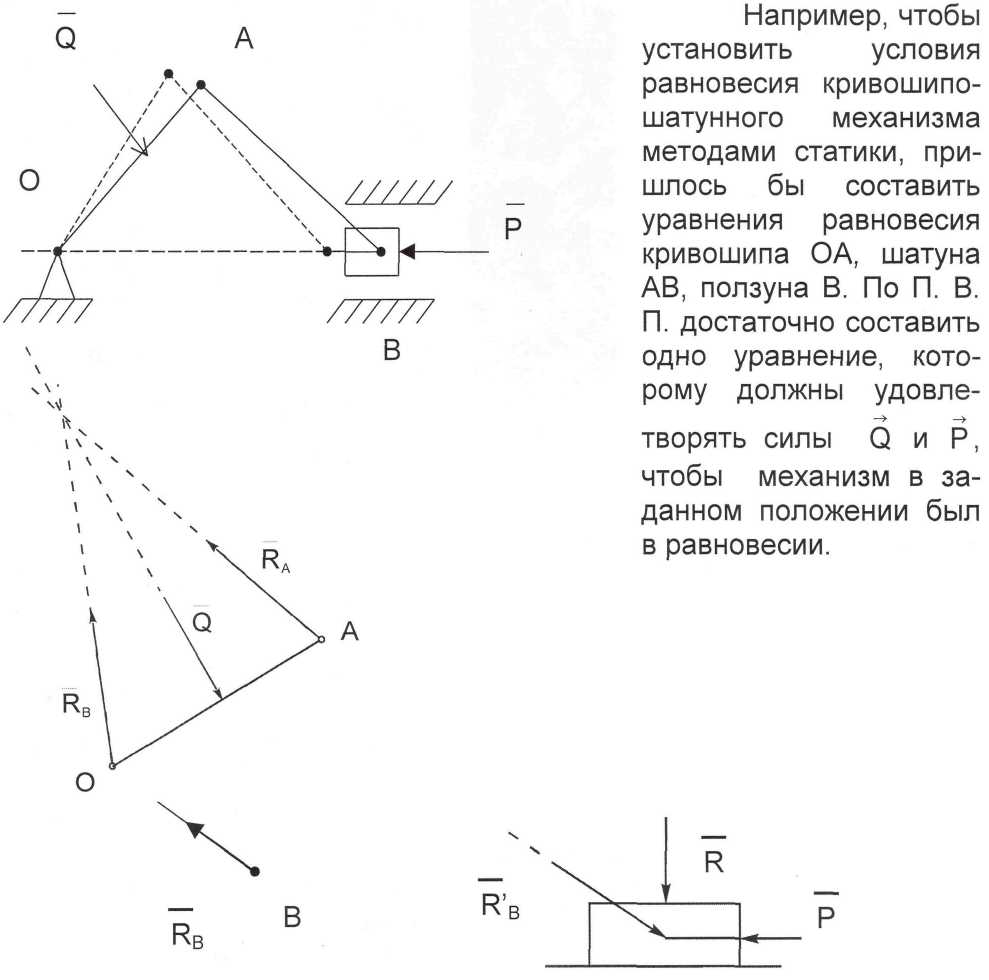
П.В.П. является ещё одним общим принципом при решении задач механики. Он устанавливает в наиболее общем виде условия равнове-сия любой механической системы. В статике для определения (записи) условий равновесия системы тел приходилось рассматривать равнове-сие каждого тела этой системы. Если тел много, то система уравнений получалась большой. При определении (записи) условий равновесия системы тел по П. В. П. рассматриваются перемещения, которые можно сообщить точкам или телам механической системы, чтобы вывести её из занимаемого равновесного положения.
Возможные перемещения точки и системы.
Действительное перемещение свободной математической точки вы-звано действующими на точку силами и начальной скоростью. Если от-влечься от сил и скоростей, то свободная математическая точка
м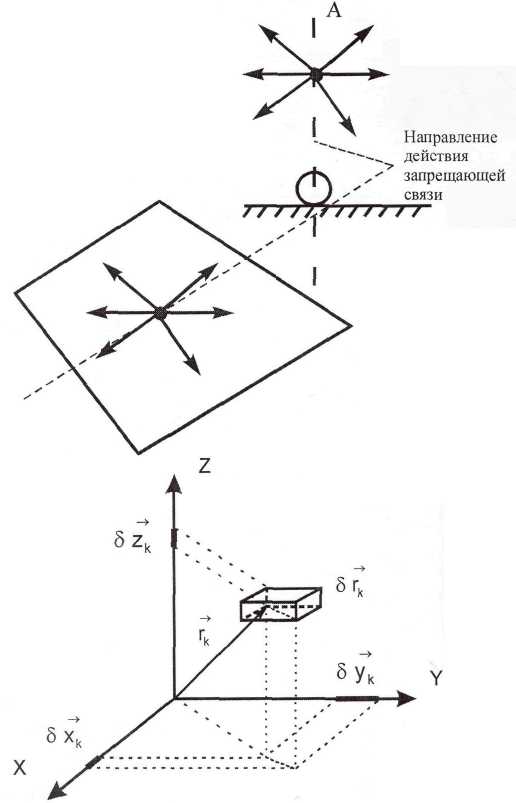 ожет
перемещаться
в лю-бом направлении. Если на точку
наложить связь, за-прещающую ей двигаться
в каком-либо направлении, то уже
не
любое перемещение точки возможно.
ожет
перемещаться
в лю-бом направлении. Если на точку
наложить связь, за-прещающую ей двигаться
в каком-либо направлении, то уже
не
любое перемещение точки возможно.

![]()

Механическая система - совокупность взаимодействующих ма-
Это взаимодействие может быть активным, а может быть в виде связи. Взаимодействие между точками твёрдого тела осуществляется связями - при любом движении тела расстояния между точками не-изменны.
На точки системы могут быть наложены внешние связи.
Например: опора О, на точку О кривошипа.
В механической системе, состоящей из свободных точек, каждая точка может иметь любые возможные перемещения, которые можно предста-вить через 3 n независимых перемещения. У такой системы 3 n степеней свободы. Связи устраняют или определяют (задают) некоторые незави-симые возможные перемещения.
Например: любое возможное перемещение точек твёрдого тела в ви-ду наличия внутренних связей можно представить (выразить) через 6 независимых перемещений. Если на это тело наложены ещё внешние связи, то независимых возможных перемещений меньше и возможных перемещений меньше.
Н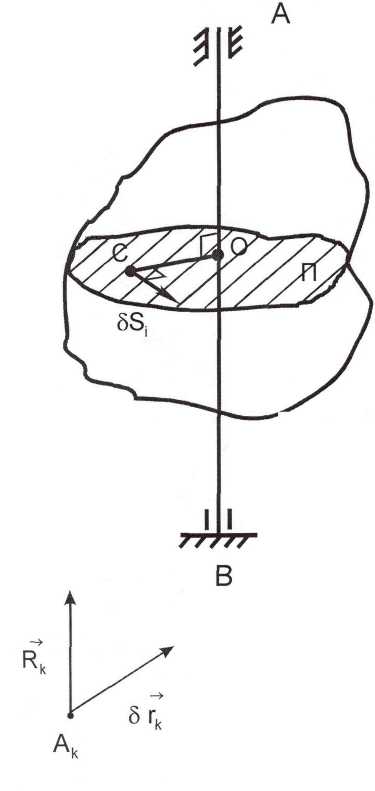 апример:
тело вращается вокруг
неподвижной
оси.
апример:
тело вращается вокруг
неподвижной
оси.
Рассмотрим какое-либо возможное переме-щение механической системы, при котором её каждая точка получает возможное перемещение
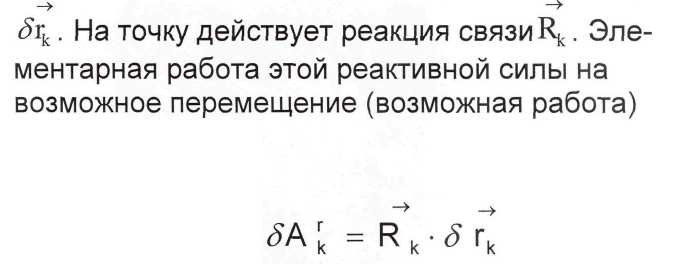
Наложенные внешние связи устранили перемещение точек на оси (т. А и т. В). Любая третья точка С тела в виду наличия ещё и внутренних связей имеет одно возможное перемещение ┴СО в плоскости перпендикулярной оси АВ. Любая совокупность бесконечно малых возможных перемещений точек системы, допускаемых наложенными связями, называется перемещением системы.
Если сумма работ реакций связей, наложенных на систему, на любом возможном перемещении равна 0, то такие связи называются идеаль-ными.
Например, внутренние связи абсолютно твёрдого тела, связь – иде-ально-гладкая поверхность при скольжении нерастяжимая нить.
Принцип возможных перемещений.
Рассмотрим механическую систему с идеальными связями, нахо-дящуюся в равновесии. Каждая точка этой системы также находится в
![]()
равновесии, поэтому
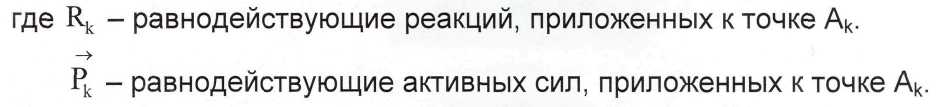

![]()
![]()
![]()
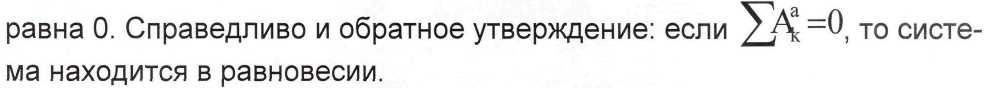
Для равновесия механической системы с идеальными связями не-обходимо и достаточно, чтобы сумма работ всех действующих на неё активных сил на любом возможном перемещении равнялась 0.
Уравнений типа (*) для систем составляют по числу степеней свободы,
т.е. для каждого независимого перемещения системы.
Если наложены не идеальные связи (с трением), то реакции этих связей
считают активными силами и используют П.В.П.
Общее уравнение динамики.
П.В.П. используют для решения задач статики о равновесии систем. Принцип Г.-Э.-Д'Аламбера решает задачи динамики методами статики. Используя оба принципа, получают ещё один общий метод решения за-дач динамики.
55
Рассмотрим систему материальных точек с идеальными связями. Если


![]()
В любой момент времени сумма работ всех активных сил и сил инерции материальных точек механической системы с идеальными связями при любом возможном перемещении равна 0. Уравнения (**) позволяют получить систему дифференциальных уравнений движения любой механической системы. Количество уравнений соответствует числу степеней свободы системы, т.е. уравнения типа (**) составляются для каждого независимого возможного перемещения системы.
56
Дифференциальные уравнения движения механической системы в обобщенных координатах.
Обобщенные координаты (перемещения)
ОК - независимые между собой параметры, однозначно представляю- щие положение механической системы в любой момент времени. Обо- значают q1, q2... qn
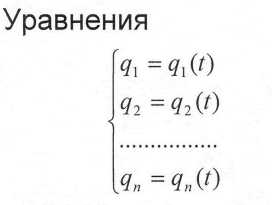
называют уравнениями движения системы в ОК.
Положение любой точки механической системы в пространстве выражается через ОК. Следовательно, для т. Ак её радиус-вектор и rk координаты xk, yk, zk являются функциями ОК
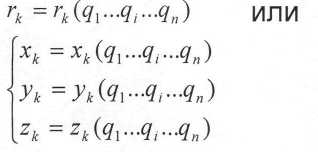
Для механической системы, у которой все связи - геометрические, т.е. дающие ограничение перемещениям точек системы, а не их скоростями, число ОК равно числу степеней свободы (ЧСС), числу независимых возможных перемещений.
![]()
Простейшей механической системой является абсолютно твердое тело. В кинематике твердого тела было установлено, что положение твердого тела полностью определяется конечным числом независимых параметров, которые и есть ОК твердого тела как механической системы.
Рассматривая кинематику каждого вида движения твердого тела, мы установили независимые параметры, через которые удобно выражать перемещения любой точки этого тела.

n=6
Эти параметры можно принимать за ОК при составлении дифферен-циальных уравнений движения этих тел в ОК.
Но можно за ОК взять и другие параметры твердого тела, только npi/ выполнении условия взаимной независимости.
ОК могут быть как угловыми, так и линейными перемещениями. Соот ветственно обобщенными скоростями qi, могут быть угловые или линейные скорости.
Механическая система с геометрическими связями состоящая из нескольких тел имеет ЧСС, т. е. число ОК, равное сумме ЧСС её отдельных тел.
Независимым считаем положение тела 1

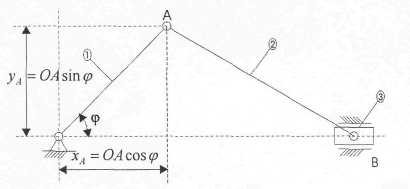
![]()
Механическая система с геометрическими связями из «м» материаль-ных точек. На точки действуют силы, F1 , F2 … Fk … Fm равнодействующие которых Система имеет «n» степеней свободы, т.е. её положение определяется «n» OK: q1...qk...qn . Дадим OK qi изохронное приращение δqi
Все остальные n-1 ОК оставим неизменными.
Система совершит независимое возможное перемещение соответст- вующее δqi
![]()
Силы, действующие на точку Ак, совершат возможную работу
![]()
![]()
Обобщенной силой (ОС) Qi; соответствующей OK q1, называется скаляр-ный множитель в выражении возможной работы всех сил системы перед приращением этой OK δqi
Т.к. ОК независимы между собой, то при произвольном возможном пе-ремещении, когда все ОК получат приращения, полная возможная работа всех сил определится как сумма возможных работ на независимых перемещений
![]()

Дифференциальные уравнения движения механической системы в ОК.
За исходное возьмем ОДУ
![]()
Для сил инерции материальных точек системы можно ввести понятие обобщенных сил инерции Qiф, Ф1,… Фk… Фm аналогичные обобщенной силе Qi
![]()
![]()
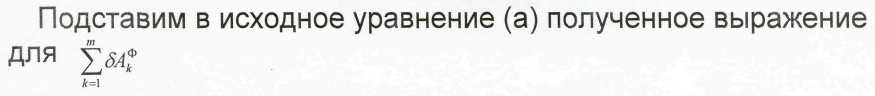
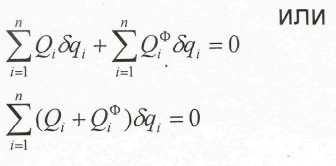
(б)
Т.к. при произвольном возможном перемещении системы все ОК одновременно не могут быть равны нулю, то уравнение выполняется, если каждый коэффициент перед δqi., будет равен 0.

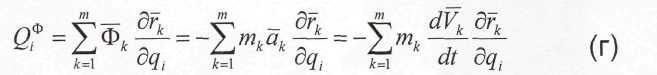
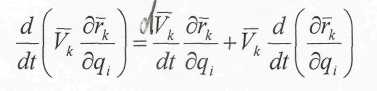
отсюда
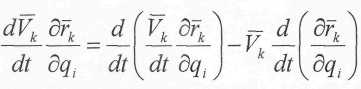
1. Свойство переместительности в последовательности взятия полных и частичных производных
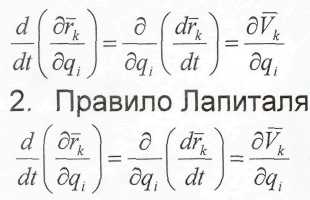
С учетом этого
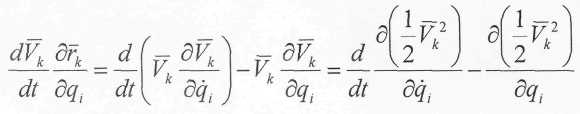
Подставим это в выражение (г)
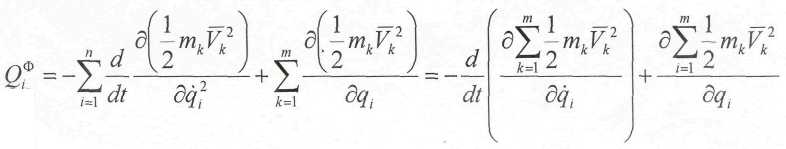
где

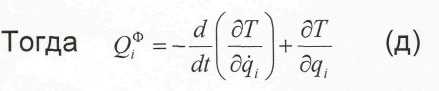
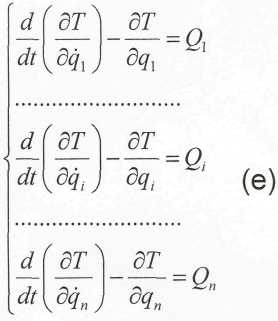
системы в ОК.

Уравнения (е) носят имя Лагранжа, их достоинство в том, что для систем с геометрическими связями число таких уравнений = ЧСС системы и обладает необходимость при исследовании движения системы определять уравнения движения каждого тела системы.
При составлении уравнении уравнения Лагранжа 2го рода в выражения обобщенных сил войдут только реакции неидеальных связей. В диффе-ренциальные уравнения движения тел системы входили бы все реак-
тивные силы и идеальных связей тоже.
Потенциальные силы.
При решении задач механики часто определяют работу силы -
динамическую меру действия силы.
В общем случае, когда F = F(t, r, v), для определения работы
необходимо знать закон движения, а именно он и не задан при решении
2— задачи динамики.
Есть вид сил, работу которых можно определить не зная r(t) закона
движения, это - потенциальные силы.
Область пространства, в которой на материальную точку действует
сила, зависящая от аргумента t и положения точки в пространстве по
отношению к системе отсчета rk называется силовым полем. Такие силы
![]()
Силовое поле, силы которого не зависят явно от t называются
стационарным. Силы стационарного поля Fk = Fk(t ,rk)
Для определения работы сил стационарного поля нет необходимости
знать законы движения материальных точек, достаточно знать
уравнение траектории в координатной форме.
Для вычисления работы по формуле
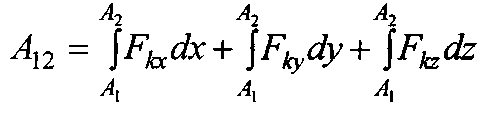
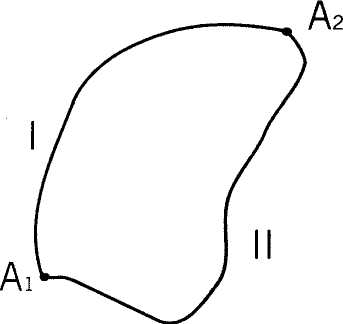
достаточно знать зависимость между хк, ук и zk Силы стационарного силового поля обладают еще одним свойством: работа этих сил на перемещение A^2 по какой-либо траектории равна работе на перемещение A2At с противоположным знаком
Свойства
сил стационарного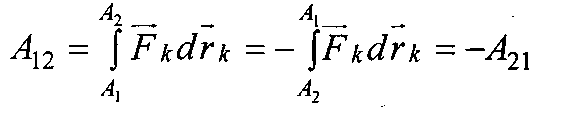 силового
поля:
силового
поля:
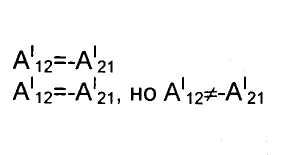
![]()
Выберем в силовом поле точку Ao(xo,yo,zo)
Величина, равная работе потенциальной силы, совершаемой при
перемещении k-ой материальной точки из положения A(x,y,z) в
Ao(xo,yo,zo) называется потенциальной энергией материальной точки
Предполагается, что в Ао, потенциальная энергия точки = 0.
Назовем эту точку нулевой. Обозначают потенциальную энергию
П(греч.)
Пк = Aaao
Потенциальная энергия, как и всякая работа силы стационарного силового поля является функцией координат Пk(x,y,z) или Пк(г). Работу потенциальной силы Fk можно определить'при перемещении A1 в А2 следующим образом
![]()
т. е. при известной Пк(х ,у ,z) работа потенциальной силы равна разности потенциальных энергий начального и конечного положений материальной точки.
Определим связь потенциальной энергии Пк с потенциальной силой Fk Дадим приращение координате х→∆х и определим изменение П. Э. на этом перемещении
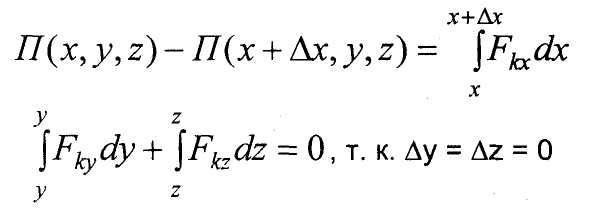
По теореме о среднем
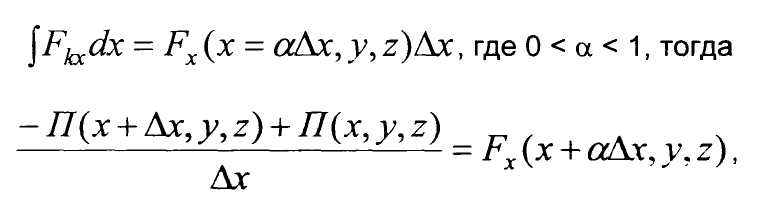
если взять предел при ∆х→0, то
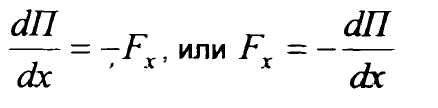
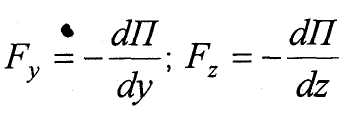
Отсюда можно получить выражения определяющие условие потенциальности сил.

Рассмотрим два вида сил
а) Сила тяжести материальной точки
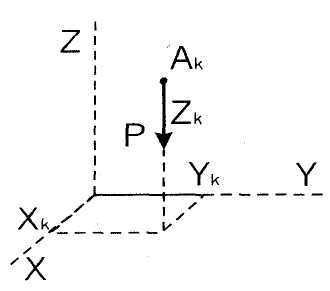
![]()
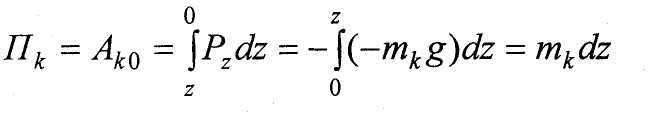
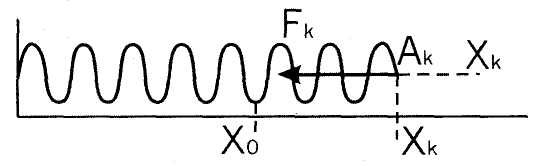
Fkx= -c(x - х0); Fky = Fkz = 0. Условия (**) выполняются Если х0- нулевая точка, то потенциальная энергия будет
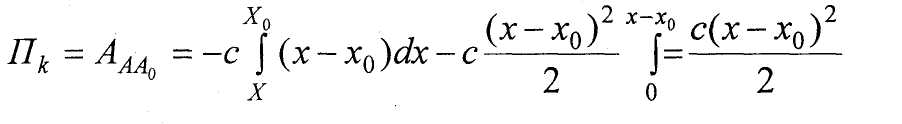
Дифференциальное уравнение в ОК в случае потенциальных
сил.
Пусть механическая система находится в потенциальном силовом поле. Материальная точка Ак системы будет иметь потенциальную энергию, определяемую ее координатами Пк = Пк(хк ,ук ,zk) или Пk = Пk(r). Потенциальная энергия системы = сумме потенциальных энергий точек системы
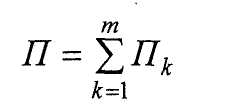
![]()
Если дадим системе произвольное возможное перемещение, то возможная работа системы будет
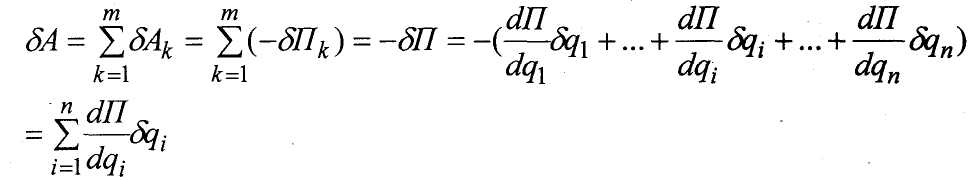
![]()
Сопоставляя эти выражения, получаем
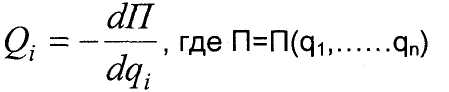
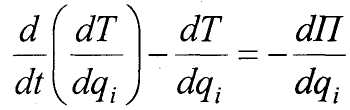
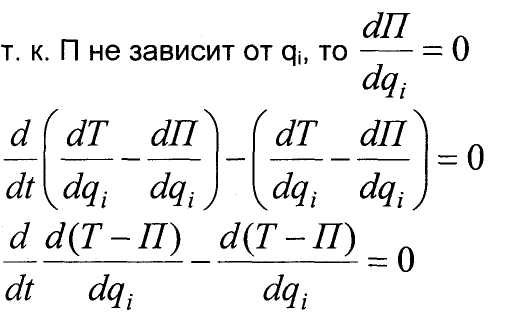
Обозначают Т-П=1_ - функция Лагранжа, или кинетический потенциал Уравнения Лагранжа для потенциальных сил: