Проанализируем амплитуду вынужденных колебаний:
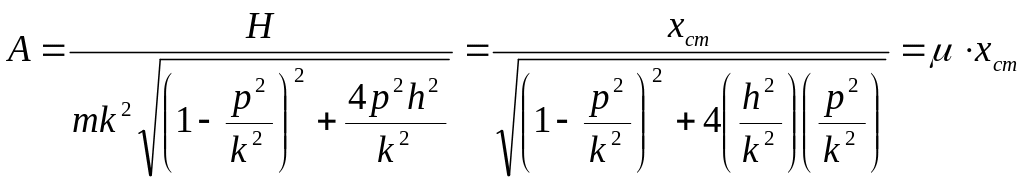
Коэффициент
динамичности, определяемый соотношением
и
Характер
зависимости
от
аналогичен
рассмотренной для вынужденных колебаний
без вязкого сопротивления. Отличие в
том, что при вязком сопротивлении (
)
при k = Р значения не бесконечны. Их
значения определяются силой сопротивления,
чем больше сопротивление (
), тем меньше резонансная амплитуда и
наступает при
.
Свободные малые колебания механической системы с
одной степенью свободы.
При действии на механическую систему восст. сил она может совершать колебательное движение около положения равновесия.
Положение равновесия, если движ. мех. сист. исследуется в обобщ. коорд., определяется уравнениями равновесия:
или 
–для консерватив. мех. сист.(*)
Равновесие различают трёх видов:
Устойчивое, когда при отклонении механической системы из положения равновесия, она стремится вернутся в него.
Неустойчивое, когда при отклонении механической системы из положения равновесия заданное отклонение увеличивается.
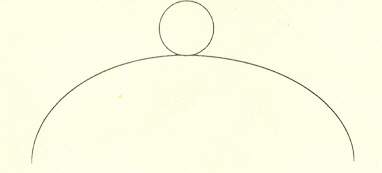
З. Безразличное, когда при отклонении механической системы из положения равновесия заданное отклонение не изменяется.
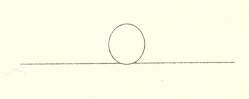
Колебания механической системы происходят около положения устойчивого равновесия.
Положение устойчивого равновесия определяется для консервативной механической системы теоремой Лагранжа-Дирихле:
В положении устойчивого равновесия потенциальная энергия минимальна
т.е. при выполнении условий (*) нужно чтобы
,
для консервативной механической системы
с одной степенью свободы.
Дифференциальное уравнение колебательного движения консервативной механической системы с одной степенью свободы можно получить из уравнения Лагранжа второго рода:
В
общем случае
,
где а(q)-обобщ. Коэффициент инерции, и
дифференциальное уравнение получается
нелинейным.
При
малых колебаниях т.е. при малых начальных
отклонениях
и
начальных скоростях
о
можно, с достаточной степенью точности,
считать
.
Потенциальную
энергию с принимаемой в этом случае
точностью можно считать
, где
с
– обобщ. коэффициент жесткости системы
При таких предпосылках дифференциальное уравнение движения примет вид
,
если
,
тогда
Таким образом колебания механической системы с одной степенью свободы описывается таким же линейным уравнением как и свободные колебания точки.
Решение и характеристики колебания аналогичны
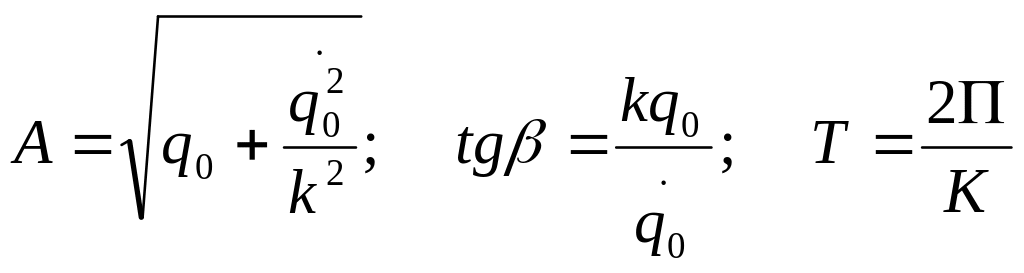
При наличии сил вязкого сопротивления и при наличии гарм. возм. силы дифференциального уравнения колебаний, их решения и характеристики имеют точно такой же вид как при аналогичных колебаниях материальной точки.