- •Динамика
- •1. Введение в динамику. Законы динамики.
- •Импульс силы
- •4. Относительное движение материальной точки.
- •Здесь – абсолютное ускорение точки по отношению к о.С.О. По теореме Кориолиса
- •8. Принцип Германа-Эйлера-д'Аламбера.
- •Динамики
- •Прямолинейные колебания материальной точки. Некоторые виды колебаний.
- •На материальную точку действуют и
- •Проанализируем амплитуду вынужденных колебаний:
4. Относительное движение материальной точки.
Основное уравнение динамики для относительного движения.
Как отмечалось раньше, второй закон динамики справедлив лишь в инерциальных системах отсчёта, т.е. в таких, в которых справедлив первый закон – закон инерции.
При исследовании сложного движения точки основная система отсчёта (о.с.о.) обычно принимается инерциальной. Поэтому для абс. движения и для переносного движения по отношению к о.с.о. справедлив II закон динамики и эти движения можно исследовать с помощью диф. ур. и теорем, полученных из основного уравнения динамики.
Если исследуется движение в неинерциальной системе отсчёта, например движение человека в автобусе, который движется с ускорением, то I и II-ой законы динамики и теоремы основанные на них будут несправедливы.
Наша задача - на примере получения уравнения движения материальной точки по отношению к неинерциальной (подвижной) системе отсчёта получить метод исследования движения в неинерциальной системе отсчёта.
П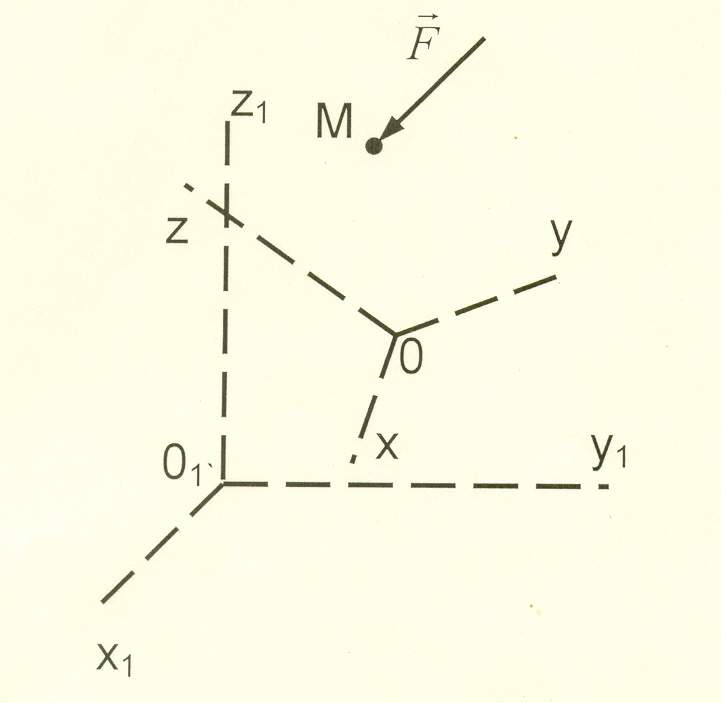 усть
известны силы, действующие на точку М
и закон движения неинерциальной
системы отсчёта по отношению к
инерциальной (подвижной по отношению
к о.с.о.)
усть
известны силы, действующие на точку М
и закон движения неинерциальной
системы отсчёта по отношению к
инерциальной (подвижной по отношению
к о.с.о.)
Система
![]() – п.с.о.;
– п.с.о.;
![]() – о.с.о.
– о.с.о.
![]() – равнодействующая
всех сил приложенных к точке М
– равнодействующая
всех сил приложенных к точке М
По
отношению к основной инерциальной
системе отсчёта
![]() справедлив закон Ньютона.
справедлив закон Ньютона.
![]()
Здесь – абсолютное ускорение точки по отношению к о.С.О. По теореме Кориолиса
![]()
Тогда
![]()
Откуда
![]()
Обозначим
![]()
Величины
![]() и
и
![]() называют переносной и кориолисовой
силами инерции.
называют переносной и кориолисовой
силами инерции.
![]()
![]()
Чтобы составить уравнение движения материальной точки в неинерциальной системе отсчёта в форме второго закона динамики надо действующим силам добавить переносную и кориолисову силы инерции.
Определение
сил инерции
и
связано с определением ускорений
![]() и
и
![]() ,
которые
вычисляются в зависимости от вида
движения П.С.О.
,
которые
вычисляются в зависимости от вида
движения П.С.О.
Если
П.С.О. движется поступательно, то
![]() ,
а
не
зависит от положения точки М по отношению
к этой системе отсчёта.
,
а
не
зависит от положения точки М по отношению
к этой системе отсчёта.
Условие относительного покоя.
Принцип относительности классической механики.
Если учесть, что относительный покой означает:
![]() и
и
![]() т.е.
и
т.е.
и
![]()
Тогда из следует
![]()
![]()
Если рассматривать относительный покой точки при выполнении условия , то это не означает, что при придании точке начальной скорости, она будет двигаться равномерно и прямолинейно.
Т.к.
во-первых,
при появлении
![]() ускорение
ускорение
![]()
Во-вторых, при относительном движении точки изменяется её положение в подвижной системе отсчёта, т.е. изменяется и нарушается условие .
Используя уравнение можно найти условие, которому должны удовлетворять системы, в которых выполняется первый закон динамики (т.е. при отсутствии сил материальная точка находится в состоянии покоя либо равномерного прямолинейного движения).
Для этого из необходимо следует
![]()
![]()
Это
уравнение удовлетворяется и при
и для
![]() , но
, но
![]() ,
при
,
при
![]() ,
т.к. в этом случае
,
т.к. в этом случае
![]() .
.
При
отсутствии сил
![]() .
.
Следовательно, подвижная система является инерциальной, если она совершает равномерное прямолинейное движение. Уравнение примет вид
![]()
т.е. соблюдается II закон Ньютона, т.е. относительное движение не отлично от абсолютного с точки зрения динамики.
Т.о. если существует хотя бы одна инерциальная система, то существует бесчисленное множество инерциальных систем. Все они по отношению друг к другу движутся равномерно и прямолинейно. Находясь в одной из них и наблюдая за движением точки нельзя установить, находится эта система в покое либо совершает равномерное прямолинейное движение. Это и есть принцип относительности классической механики, который лежит в основе теории относительности.
5. Введение в динамику механической системы.
Механическая система—совокупность взаимодействующих материаль-ных точек или тел.
Абсолютно твердое тело—непрерывная совокупность материальных то-чек, расстояния между которыми всегда неизменны—тоже механическая система.
Например: машина или механизм, в котором все тела связаны геомет-рическими связями. На все тела действуют силы взаимодействия. А группа летящих самолетов систему не образует.
Внешние и внутренние силы.
Силы, действующие на точки механической системы разделяют на ак-тивные и реактивные, внешние и внутренние.
Внешними называются силы, действующие на тела или точки системы со стороны тел, не входящих в состав данной системы. Внутренними называются силы, действующие на точки системы со стороны других точек этой же системы. Обозначают:
Fe—внешние (экстерьер, фр.)
![]() внутренние
(интерьер)
внутренние
(интерьер)
Понятия относительные и зависят от того, что мы включили в рассмат-риваемую систему.
Свойства внутренних сил.
По третьему закону Ньютона силы взаимодействия любых двух точен механической системы равны по модулю и противоположны по направ-
![]()
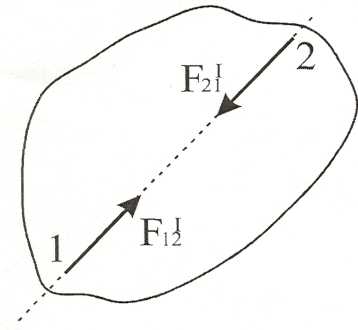
1. Геометрическая сумма всех внутренних
сил системы = 0.
![]()
2. Сумма моментов всех внутренних сил системы относительно любого центра или оси = 0.
![]()
Однако отсюда не следует, что внутренние силы уравновешены. Т. к. Внутренние силы приложены к разным точкам и они могут перемещаться под действием этих сил, то про их уравновешенность говорить нельзя.
Масса системы. Центр масс.
Из второго закона динамики следует, что движение точек системы, а следовательно и самой системы зависит от массы этих точек. Движение системы зависит также от того, как распределены в пространстве массы точек. Введем два понятия:
Масса системы—величина, равная сумме масс материальных точек, об-
разующих систему
![]()
М—масса системы,
mk—масса k-ой материальной точки системы.
Центр масс системы—геометрическая точка, положение которой харак-теризует распределение массы системы в пространстве. Положение центра масс определяется радиус-вектором, rс который равен
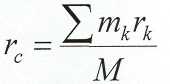
Отсюда видно, что, изменяя положение точек системы, изменяем поло-жение центра масс системы.
Положение центра масс в декартовой прямоугольной системе координат определяется координатами хс, ус, zc, которые являются координатами гс, если начало координат поместить в центр.

Положение центра масс и центра тяжести совпадают, если все точки системы находятся в однородном поле сил тяжести.
Момент инерции относительно оси.
Положение центр масс характеризует распределение массы системы для определения движения системы не полностью. Этой характеристики достаточно только для определения поступательного движения. Момент инерции относительно оси (Jz) является мерой инертности тела при его вращении относительно этой оси. Эта характеристика для вращательного движения имеет такое же значение, как масса системы для поступательного движения.
Момент инерции системы относительно оси (Jz) - величина, равная сумме произведений масс всех материальных точек системы на квадрат
![]()
![]()
все точки системы не могут быть на
и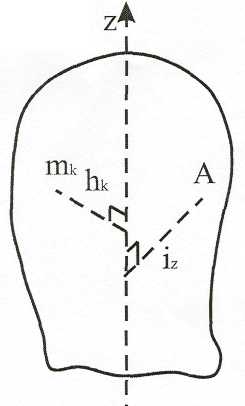 х
расстояний до этой оси.
х
расстояний до этой оси.
оси z.
Для удобства определения момента инерции системы введено также понятие радиуса инерции. iz—линейная величина, квадрат которой равен отношению момента инерции системы к ее массе.
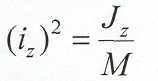
iz—расстояние от точки системы, в которой надо со-средоточить всю массу системы М, чтобы момент инерции этой точки относительно оси z был =JZ.
Момент инерции относительно оси системы, образованной несколькими телами определяют, как сумму моментов инерции этих тел относительно той же оси.
В справочной литературе есть данные о Jz тел простой формы относи-тельно осей, проходящих через центр масс (центральных осей). Тела сложной формы можно разбить на части и воспользоваться данными справочника. Для этого нужно уметь вычислять моменты инерции относительно осей не центральных.
Перейти при определении Jz от центральной оси к другой, ей позволяет теорема Гюйгенса.

![]()

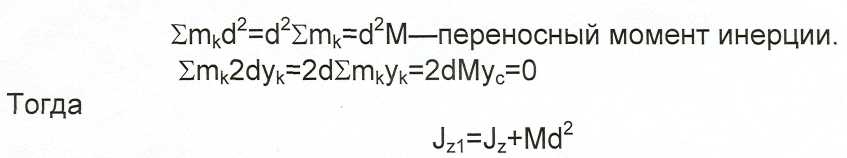
Из всех моментов инерции относительно параллельных осей собственный момент инерции - минимальный.
Вычислим момент инерции некоторых однородных тел. а) Тонкий однородный стержень.
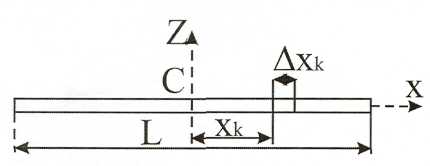
![]()
Масса стержня-М , длина—I Определить J7
![]()
![]()
Его масса
![]()
![]()

Момент инерции относительно конца определим по теории Гюйгенса.
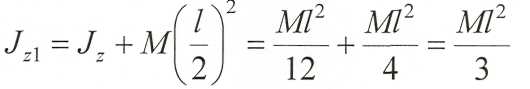

![]() Масса
кольца М, радиус R.
Определить Jz,
Масса
кольца М, радиус R.
Определить Jz,
плоскости кольца и проходит через центр масс кольца.
Все точки кольца находятся на расстоянии R от оси, тогда
![]()
Так же определяется Jz для полого цилиндра с тон-
кой стенкой.
с) Тонкая однородная круглая пластина.
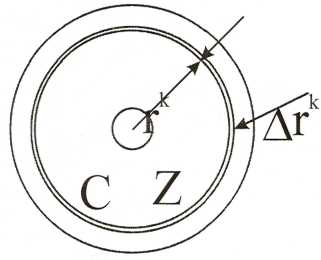
М—масса пластины, R—радиус.
![]()
—масса единицы площади пластины.
![]()
![]()
![]()
В пределе при
![]()
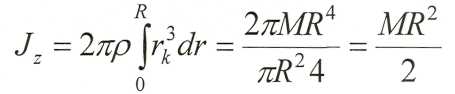
Его масса будет:
По этой формуле определяем Jz для сплошных однородных цилиндров.
Дифференциальные уравнения движения механической системы.
Рассмотрим механическую систему, состоящую из "n" материальных то-
![]()

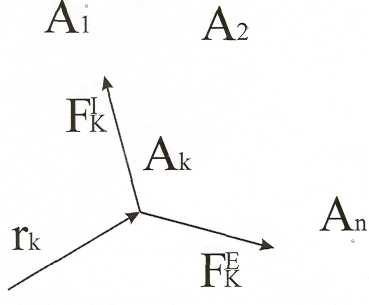
Для механической системы таких уравнений будет "n". Они будут определять закон движения всех точек.
Эта система уравнений называется дифференциальным уравнением движения механической системы.
В координатной форме движение точки Ак определяется тремя дифференциальными уравнениями.
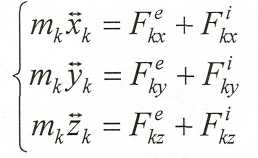
Для всей системы таких уравнений будет Зn штук. Т. к. на практике внут-ренние силы часто неизвестны, а система получается громоздкой, то решают ее в исключительных случаях.
Практического значения дифференциальные уравнения движения меха-нической системы не имеют. Они используются только для вывода об-щих теорем динамики системы, как исходные.
С помощью этих теорем можно найти общие характеристики движения механической системы.
6. Общие теоремы динамики механической системы. Теорема о движении центра масс.
В некоторых задачах определяется закон движения центра масс меха-нической системы. Для получения дифференциального уравнения дви-жения центра масс просуммируем левые и правые части дифференци-ального уравнения движения механической системы по всем точкам системы.
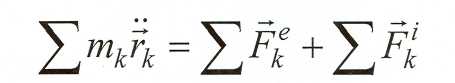
По
свойству внутренних сил![]()
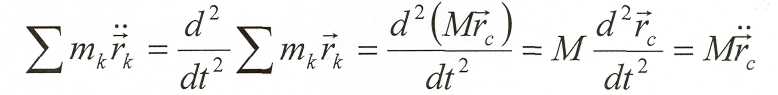

![]()
Итак
, по определению центра масс.
Центр масс механической системы движется как материальная точка, масс которой равна массе всей системы, и к которой приложены все внешние силы системы.
В координатной форме дифференциальных уравнения движения центра масс примут вид:
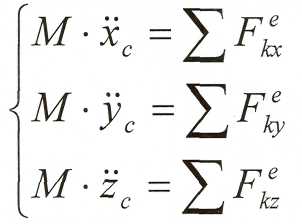
равен
нулю, то
![]()
![]()
т.е. центр масс или движется прямолинейно с постоянной скоростью или находится в покое
![]()
но
его![]()
![]()
, то
![]()
![]() или
или
![]()
![]()
,
приложенных к твердому телу, не может
изменить движение центра масс т.к.
Количество движения механической системы.
У механической системы, как и у материальной точки, есть две меры движения - количество движения и кинетическая энергия. Количество движения механической системы есть векторная величина равная сумме количеств движения всех материальных точек системы.
![]()
![]()
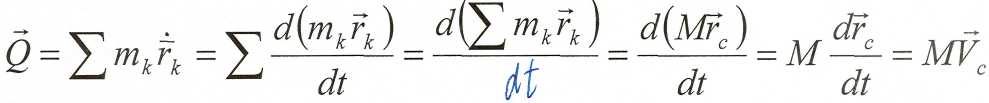
,
итак
![]()
Количество движения системы равно произведению массы всей системы на скорость центра масс.
Следовательно, количество движения системы характеризует только поступательное движение системы вместе с её центром масс. Если движутся точки системы, а центр масс не перемещается, то количество движения системы равно нулю (Q = 0).

от
![]()
![]()
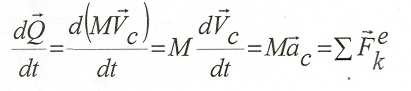
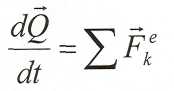
Это уравнение выражает математически дифференциальную форму
теоремы
об
изменении![]()

Следствия из теоремы об изменении количества движения механической системы.
![]()
за некоторый проме-
жуток времени равен нулю, то количество движения системы в этот промежуток времени постоянно.
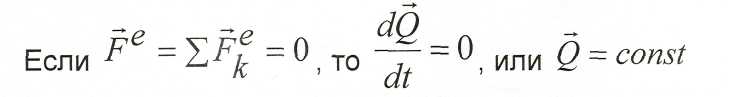
2. Если проекция главного вектора внешних сил в течение некоторого промежутка времени на какое-то направление равно нулю, то проекция количества движения на это направление в течение этого промежутка времени постоянна.
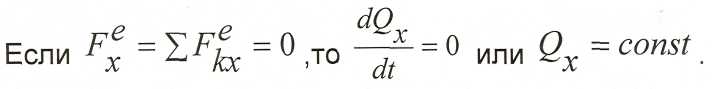
Эти два следствия выражают закон сохранения количества движения механической системы. Из них следует, что внутренние силы не могут изменить количество движения системы в целом. Получим теорему в интегральной или конечной форме. Проанализируем математическую запись дифференциальной формы теоремы от
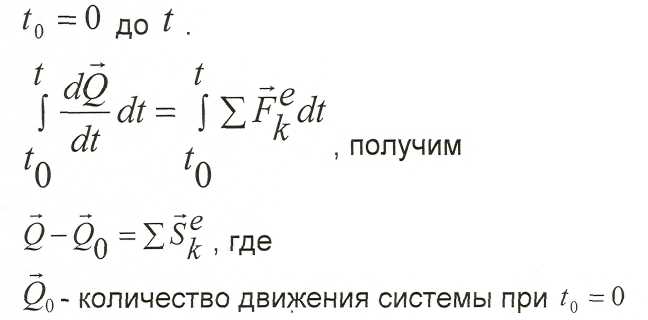
Q - количество движения системы при t

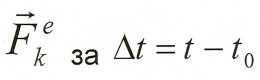
В координатной форме можно записать
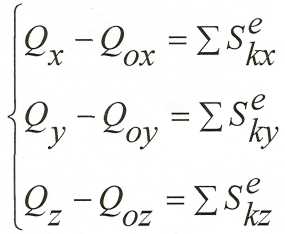
Изменение количества движения механической системы (его проекции) за некоторый промежуток времени равно импульсу всех внешних сил (их проекций) за этот же промежуток времени.
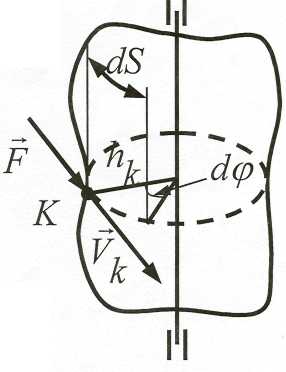
Теорема Эйлера (применение к сплошным средам).
Пусть некоторая сплошная среда (жидкость, газ) движется внутри трубы переменного сечения.
П ри
установившемся движении масса среды,
протекающая через любое поперечное
сечение за
единицу
времени (секундная масса) посто-
ри
установившемся движении масса среды,
протекающая через любое поперечное
сечение за
единицу
времени (секундная масса) посто-
;
МКГС
За
промежуток времени dt
изменение
количества
движения
среды в объеме
первоначально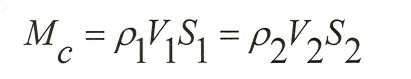
![]()

![]()
или
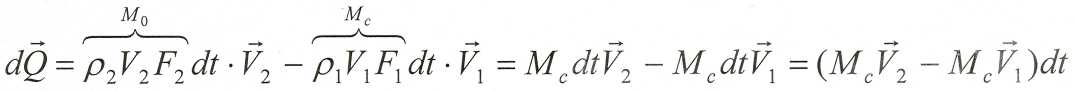
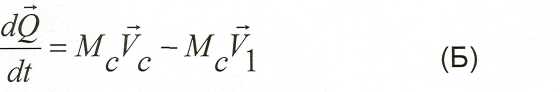
Но нами уже получено
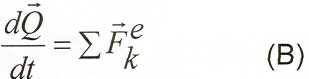


В координатной форме можно записать
![]()
Теорема об изменении главного момента количества движения системы.
Главный момент количества движения механической системы относительно центра или оси есть величина, равная сумме моментов количества движения всех материальных точек системы относительно этого центра или оси.

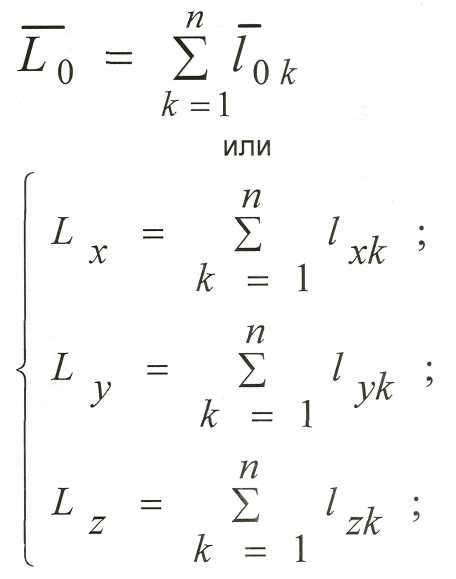
характеризует поступательное движение сис-
темы вместе с ц.м., т.е. является мерой поступательного движения. Аналогично момент количества движения является мерой вращения ме-ханической системы относительно оси (х) или сферического движения относительно центра О.
Чтобы лучше понять смысл этих величин, определим момент количества движения абсолютно твёрдого тела(системы) вращающегося вокруг
оси Z, относительно этой оси (Lz)

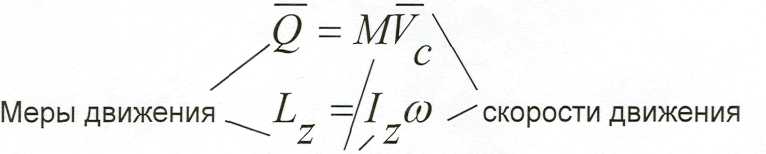
По теореме об изменении момента количества движения

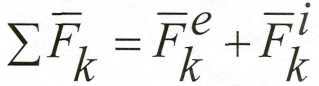

Просуммируем по всем точкам выражение (а)
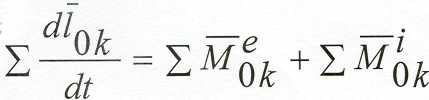
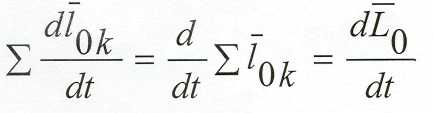
![]()




Эти уравнения выражают теорему об изменении главного момента количества движения системы, (кинетического момента)
Следствия из теоремы.
1. Если главный момент внешних сил относительно центра остаётся всё время равный нулю, то главный момент количества движения системы относительно этого центра остаётся постоянным.
![]()
2. Если главный момент всех внешних сил относительно некоторой оси остаётся всё время равен нулю, то главный момент количества движения системы относительно этой же оси остаётся постоянным.
![]()
3. Внутренние силы не могут изменить главный момент количества движения.
Например (закон сохранения)
Система вращается вокруг оси Z. Если система неизменяемая, т.е. расстояние между точками системы не изменяется, то при
![]()
![]()
т.е. точки удалились от оси вращения z, то
угловая скорость вращения уменьшится, ес-
![]()
(фигурист во вращении).
Кинетическая энергия системы.
Кинетическая энергия системы - величина, равная сумме кинетических
энергий материальных точек системы.
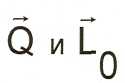
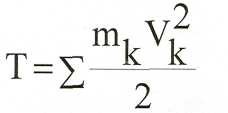
В отличие от
Т характеризует и поступательное и вращатель-
ное движение механической системы, но не отражает изменения направления движения.
Ещё одно отличие: на изменение Т оказывают влияние как внешние так и внутренние силы.
Если система состоит из нескольких тел, то кинетическая энергия системы равна сумме кинетических энергий этих тел.
![]()
Выразим кинетическую энергию системы «п» материальных точек через характеристики инертных свойств и кинематические характеристики

движения.
![]()
ется радиус вектором
Положение точки Ак системы определя-
Движение точек системы представим в виде совокупности поступательного движения вместе с центром масс (точка С) и относительного движения по отношению к центру масс.
![]()
Скорость т. АК


Это математическое выражение теоремы Кёнига о кинетической энергии механической системы.
Кинетическая энергия твёрдого тела при поступательном движении.
,
то
![]()
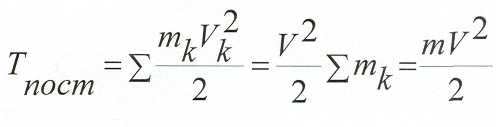
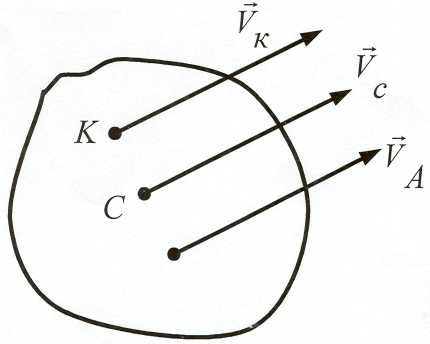
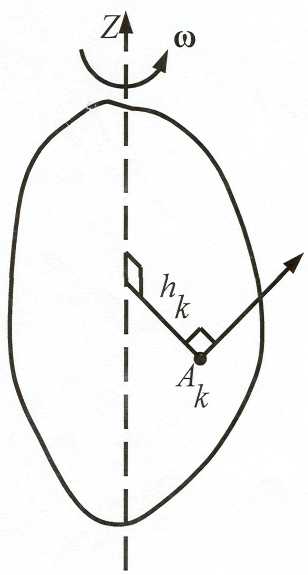
Кинетическая энергия твёрдого тела при вращении.
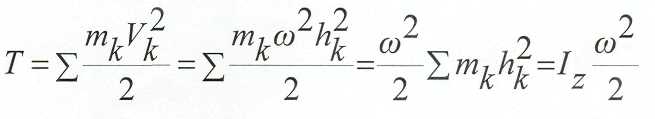
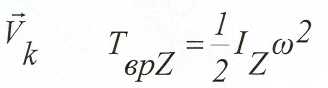
Кинетическая энергия твёрдого тела плоскопараллельного движения.
Любое плоское движение можно представить как поступательное движение вместе с центром масс и вращение относительно оси Z проходя-
щей через центр масс перпендикулярно плоскости движения. Тогда по теореме Кёнига

Кинетическая энергия поступательного движения тела вместе с центром масс.
Кинетическая энергия тела относительно оси Zc проходящей через центр масс перпендикулярно плоскости движения.
Кинетическая энергия тела при сферическом движении.
Сферическое движение можно представить как вращение вокруг мгновенной оси Q, проходящей через неподвижную точку.
-
момент инерции тела относительно
мгновенной оси вращения, ве-
![]()
личина переменная.
-
мгновенная
угловая скорость вращения
тела - переменная
величи-![]()
Кинетическая энергия свободного тела.
Движение свободного тела можно представить как совокупность поступательного движения вместе с центром масс и сферического движения относительно центра масс.
-
момент
инерции тела относительно
мгновенной
оси вращения Q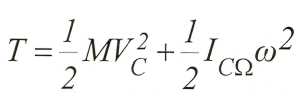
![]()
Теорема об изменении кинетической энергии системы.
Для к— точки механической системы по теореме об изменении её кинетической энергии

 Здесь
Здесь
Просуммируем по точкам системы



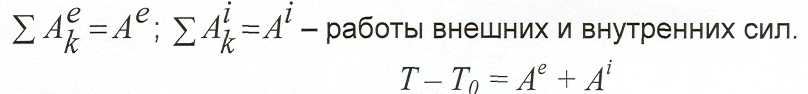
Изменение кинетической энергии механической системы на её некотором перемещении равна сумме работ внешних и внутренних сил, действующих на
м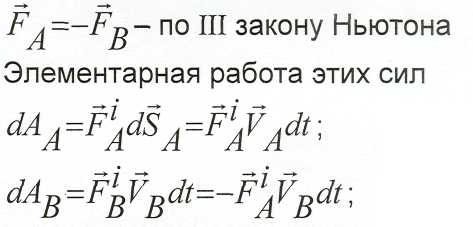 атериальные
точки системы на том перемещении.
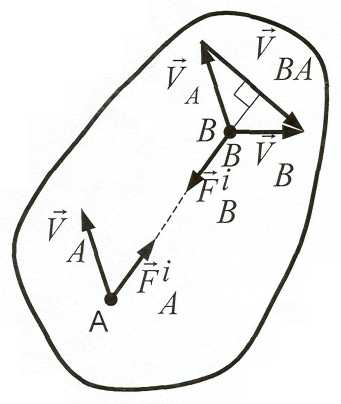
Определим работу внутренних сил,
приложенных к точкам (А и В) абс.
твёрдые тела.
атериальные
точки системы на том перемещении.
Определим работу внутренних сил,
приложенных к точкам (А и В) абс.
твёрдые тела.
Свободное движение твёрдого тела можно представить, как поступательное движение с полюсом и сферическое движение около полю-

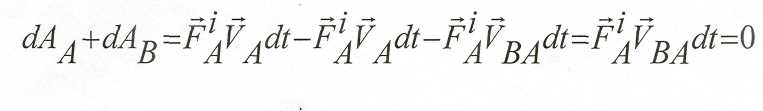


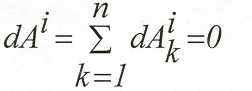
Это положение справедливо для всех неизменяемых систем. Аналогично доказывается для гибких нерастяжимых нитей.
![]()
Т.о. для неизменяемых систем теорема об изменении кинетической
энергии будет
![]()
Теорема об ∆T удобно использовать для систем неизменяемых или со-
![]()
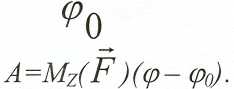

![]()
![]()
![]()