Детерминанты

Пусть – коммутативное кольцо с единицей 1. Рассмотрим квадратную матрицу -го порядка 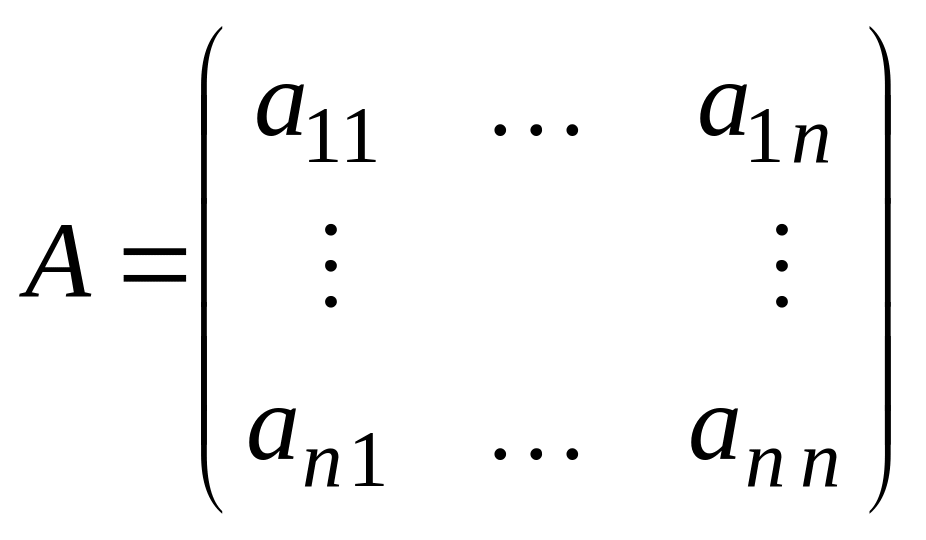, каждый элемент этой матрицы является элементом кольца . Будем говорить, что матрица задана над кольцом ,

Детерминант (определитель) матрицы определим следующим образом:

(1)

где – определитель -го порядка, полученный вычеркиванием первой строки и -го столбца матрицы . называется минором -го порядка матрицы или дополнительным минором к элементу .

Пусть ( ) и ( ) – -элементные подмножества множества . Минором -ого порядка матрицы называется определитель, расположенный на пересечении строк с номерами из и столбцов с номерами из , т. е. =det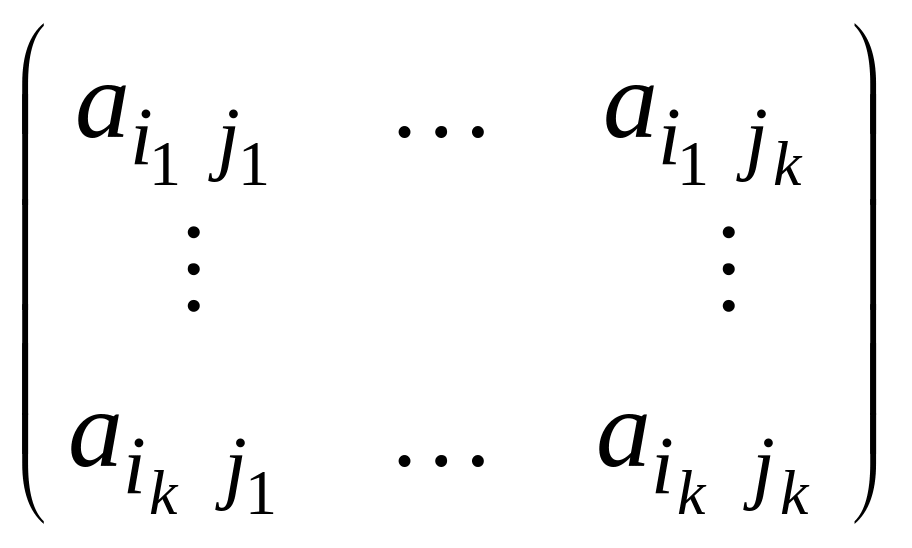 . Минор , полученный после вычеркивания из матрицы строк с номерами из и столбцов с номерами из , называется дополнительным минором к минору . Заметим, что = .

Пусть , тогда по формуле (1) получаем, что .

Теорема 1. Пусть (2)

. (3)

Тогда для любых и . (Формулы (2) и (3) называют разложением определителя по -му столбцу и -ой строке соответственно).

Доказательство. Докажем теорему методом математической индукции по . Несложно проверить справедливость формул при (сделайте это!). Далее предполагая, что формулы (2) и (3) выполнены для определителей -го порядка, докажем их справедливость для определителей -ого порядка, где . Покажем сначала, что

= . Разложив минор по первой строке, получаем . Тогда =

= = .

С другой стороны, = . Раскладывая минор по первому столбцу, получаем . Значит, == = . Так как полученные выражения различаются только порядком суммирования, то показано, что .

Прежде чем доказывать общий случай теоремы 1, дадим следующее определение.

Матрица называется транспонированной к матрице , если для любых и элементы этих матриц связаны соотношениями . Говорят также, что матрица получается транспонированием матрицы .

Докажем, что при транспонировании квадратной матрицы ее определитель не меняется.

Действительно, разложение по первой строке и разложение по первому столбцу совпадают.

, так как при .

Заметим теперь, что для доказательства теоремы, достаточно доказать, что для любого .

+ = .

=

= .

Так как

, получаем . Теорема доказана.

Пусть и , тогда произведение называется алгебраическим дополнением минора в определителе матрицы , будем обозначать его как .

Следствие 1. . (4)

Следствие 2. Для любого

= . (5)

Свойства определителя

Соотношение (4) дает нам одно из важных свойств определителя, устанавливающих равноправность строк и столбцов в определителе. Поэтому все дальнейшие свойства, устанавливаемые для строк, будут иметь место и для столбцов. Итак,

Свойство 1. При транспонировании матрицы определитель не меняется.

Свойство 2. При транспозиции (перестановке) двух строк определитель меняет знак.

Доказательство. Пусть – матрица, полученная из матрицы перестановкой первой и -ой строк. Согласно следствию 2 имеем, что . Легко проверить, что , тогда .

Итак, перестановка строк меняет знак определителя. Перестановку -ой и -ой строк в определителе можно проделать за три шага: . Свойство доказано.

Пусть – -ая строка матрицы .

Свойство 3. Если найдется пара и такая, что и , то определитель равен нулю.

Доказательство. Пусть в матрице найдется при некотором , что . Действительно, в силу (5) имеем, , но тогда замечая, что для любых и таких, что , получаем .

В том случае, если , то воспользовавшись свойством 2 и поменяв местами первую и -ую строки, сведем доказательство к уже разобранному случаю. Свойство доказано.

Свойство 4. Если все элементы некоторой строки матрицы умножить на элемент , то и сам определитель умножится на .

Доказательство. Пусть – матрица, полученная из матрицы умножением каждого элемента -ой строки на элемент , тогда . Действительно получаем, что . Свойство доказано.

Свойство 5. Если , то , где

.

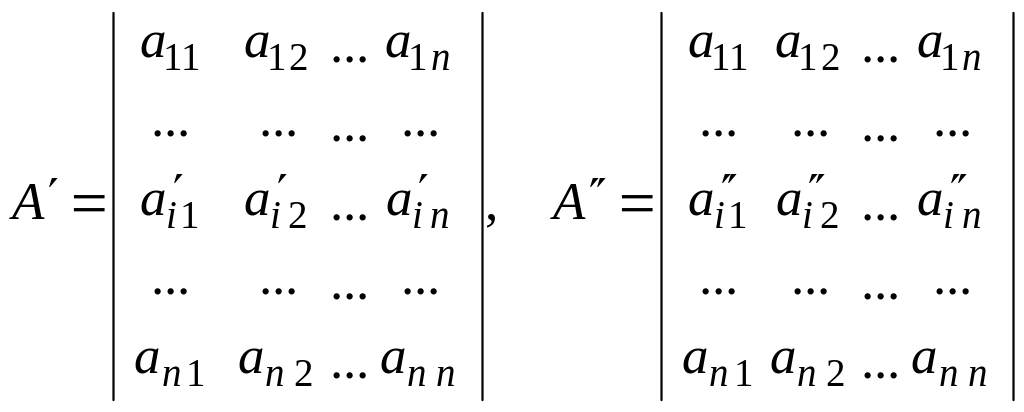Доказательство. Действительно,

, что и требовалось доказать.

Свойство 6. Пусть , тогда , если , то , где – матрица, -ая строка которой равна .

Доказательство провести индукцией по .

Свойство 7: Определитель не изменится, если к строке прибавить линейную комбинацию остальных строк.

Доказательство. Пусть – матрица, полученная из матрицы прибавлением к -ой строке линейной комбинации других строк. Так как , то по свойству 5 имеем , где – матрица, для которой .

Применяя свойство 6, имеем, что , где – матрица, -ая строка которой есть , причем . Так как каждая из матриц есть матрица, в которой строка повторяется дважды, по свойству 3 получаем, что , значит . Следовательно, , что и требовалось доказать.