3.6. Фундаментальні послідовності. Критерій Коші

Означення. Кажуть, що послідовність задовольняє умові Коші або є фундаментальною, якщо для .

Теорема. Якщо фундаментальна, то вона обмежена.

Доведення.

Дійсно, візьмемо . Візьмемо . Якщо , то . Таким чином, при всі члени послідовності знаходяться в околі точки радіуса 1, а поза цим околом знаходиться лише скінченне число членів послідовності. Отже, вся ця послідовність обмежена.

Теорема Коші (критерій збіжності Коші). Для того, щоб послідовність була збіжною, необхідно і достатньо, щоб вона була фундаментальною.

Доведення.

Необхідність. Нехай збіжна і . Доведемо фундаментальність .

Нехай , тоді, оскільки , то знайдеться таке число . В якості візьмемо , тоді . Отже, – фундаментальна.

Достатність. Нехай - фундаментальна. Тоді .

Так як фундаментальна послідовність обмежена, то у неї є збіжна підпослідовність . Нехай . Тоді для того ж

.

Позначимо через . Нехай , де . Тоді при

.

Отже, .

3.7. Найбільша і найменша часткова границя

Означення. Границя підпослідовності даної послідовності називається її частковою границею.

Теорема. В розширеній множині дійсних чисел множина часткових границь послідовності має найбільший і найменший елемент.

Позначення: – нижня (найменша часткова) границя;

– верхня (найбільша часткова) границя.

Теорема. Послідовність збігається в тоді і тільки тоді, коли її нижня границя дорівнює її верхній границі.

4. Границя і неперервність функції

4.1. Основні елементарні функції

1. .

2. .

3. .

4. .

5. .

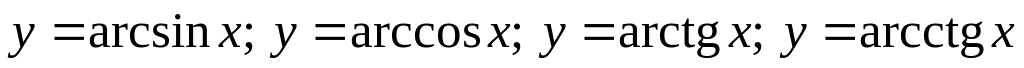6. Гіперболічні функції:

– гіперболічний косинус;

– гіперболічний синус;

– гіперболічний тангенс;

– гіперболічний котангенс.

Деякі основні властивості гіперболічних функцій:

1. 

2. 

3. 

4. 

5. 

Означення. Функція називається елементарною, якщо вона може бути явним чином задана за допомогою формули, що містить лише скінченне число арифметичних дій і суперпозицій основних елементарних функцій.

Всі елементарні функції поділяються на класи:

1. Многочлени: .

2. Дробово-раціональні: , де - многочлени, причому ‑ ненульовий многочлен.

3. Ірраціональні – функції, що не є раціональними, і які можуть бути задані за допомогою суперпозицій скінченого числа раціональних функцій, степеневих функцій з раціональними показниками та чотирьох арифметичних дій.

4. Трансцендентні – елементарні функції, що не є ні раціональними, ні ірраціональними (логарифм, синус і т. ін.)

Приклади неелементарних функцій.

1. Функція Діріхле:

2. Функція знака:

.

4.2. Границя функції

Означення. Проколотим -околом точки називається її -окіл, з якого вилучена сама точка , тобто

.

Нехай функція визначена на множині , і – гранична точка цієї множини.

Означення границі за Гейне. Точка називається границею функції при прямуючому до (в точці ), якщо для будь-якої послідовності , послідовність має своєю границею точку , тобто .

У цьому випадку пишуть .

Означення границі за Коші. Точка називається границею функції при прямуючому до (в точці ), якщо .

У цьому випадку пишуть .

Теорема. Означення границі функції за Коші і за Гейне еквівалентні.

Доведення.

1. Нехай за Коші. Доведемо, що за Гейне.

Нехай послідовність така, що , . Тоді, оскільки має границю за Коші, то .

Для , .

2. Нехай за Гейне. Доведемо, що за Коші.

Припустимо супротивне, тобто . Нехай , тоді , .

Таким чином, ми вказали послідовність , , яка збігається до , тобто . Ми прийшли до суперечності, значить за Коші.

Розглянемо випадок, коли .

За Гейне: Нехай визначена на множині , яка не обмежена зверху. Кажуть, що , якщо .

За Коші: , якщо для , .