8.4. Асимптоты графика функции

При исследовании поведения функции на бесконечности, т.е. при , или вблизи точек разрыва второго рода, часто оказывается, что график функции сколь угодно близко приближается к той или иной прямой. Такие прямые называют асимптотами.

Определение. Асимптотой графика функции называется прямая, обладающая тем свойством, что расстояние от точки (х,f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.

Теорема (необходимый и достаточный признак существования вертикальной асимптоты). Пусть функция у= f(x) определена в некоторой окрестности точки х₀ и хотя бы один из пределов функции при (слева) или при (справа) равен бесконечности. Т.е. или тогда прямая х=х₀ является вертикальной асимптотой графика функции у=f(x).

Прямая х=х₀ не может быть вертикальной асимптотой, если функция непрерывна в точке х₀ т.к. в этом случае . Следовательно вертикальные асимптоты х=х₀ следует искать в точках разрыва функции у=f(x) или на концах ее области определения (a,b), если a и b – конечные числа.

Пример. Найти вертикальные асимптоты графика функции .

Данная функция имеет единственную точку разрыва (значение не определено).

Т.к. , то прямая – единственная вертикальная асимптота.

Займёмся нахождением наклонных асимптот, уравнения которых можно записать в виде .

Теорема (необходимый и достаточный признак существования наклонной асимптоты). Пусть функция у= f(x) определена при достаточно больших х и существуют конечные пределы и , Тогда прямая у=kx+b является наклонной асимптотой графика функции у=f(x).

Теорема. Пусть функция у= f(x) определена при достаточно больших х и существует конечный предел , Тогда прямая у=b является горизонтальной асимптотой графика функции у=f(x).

8.5. Схема полного исследование функции методами дифференциального исчисления и построения её графика

Исследование функции и построение её графика рекомендуется проводить по следующей схеме:

1. Найти область определения функции.

2. Выяснить, является ли функция чётной, нечётной, периодической. При наличии какого–либо из этих свойств можно использовать симметрию при построении графика.

3. Исследовать функцию на непрерывность. Найти точки разрыва функции и её односторонние пределы в этих точках.

4. Определить асимптоты графика и поведение функции на границе области определения

5. С помощью производной первого порядка найти промежутки возрастания и убывания, найти экстремумы функции.

6. С помощью производной второго порядка найти промежутки выпуклости и вогнутости графика функции, точки перегиба.

7. Используя результаты исследования, построить график функции. При необходимости можно дополнительно найти значения функции в некоторых точках из тех промежутков, для которых предыдущие пункты исследования дали недостаточно информации.

Пример решения типовой задачи

Исследовать функцию f(x) и построить ее график

Решение:

1. Область определения функции является множество всех вещественных чисел, кроме х=1 (в этом случае знаменатель обращается в нуль), т.е.

2. Выясним, является ли данная функция четной, нечетной, общего вида:

- функция общего вида.

3. Выясним характер разрыва функции при . Для этого рассмотрим односторонние пределы функции в точке :

, .

Полученный результат говорит о том, что точка является точкой разрыва 2-го рода для данной функции, а прямая с уравнением – вертикальной асимптотой графика функции.

4.Найдем наклонные асимптоты графика функции.

Следовательно, график функции имеет наклонную асимптоту: у=х+1.

5. Найдем точки экстремума функции и определим интервалы возрастания и убывания функции.

Для нахождения точек возможного экстремума вычислим первую производную функции, прировняем ее к нулю, найдем критические точки, и интервалы возрастания и убывания.

Получаем, что функция возрастает на интервалах: , и убывает: , .

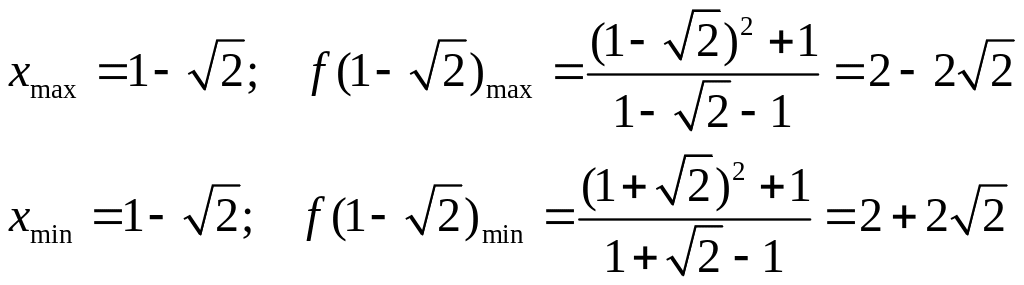
6. Найдем точки перегиба графика функции и определим интервалы выпуклости и вогнутости графика функции. Для этого найдем производную второго порядка, прировняем ее к нулю.

Т.к. вторая производная в нуль не обращается, то критических точек нет.

7. Используя полученные результаты, строим график функции